机器学习之一个变量的线性回归

• 模型表示
• 成本函数
• • 成本函数 Intuition I
  • 成本函数 Intuition II
• 梯度下降
• • 梯度下降 Intuition
• 线性回归的梯度下降

模型表示

为了建立供将来使用的符号，我们将使用 x ( i ) x^{(i)} x(i)表示“输入”变量，也称为输入要素，并且
y ( i ) y^{(i)} y(i)表示我们试图预测的“输出”或目标变量。一对 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)) 被称为训练示例，而我们将用来学习的数据集——m个训练示例的列表 ( x ( i ) , y ( i ) ) ; i = 1 , . . . , m (x^{(i)},y^{(i)});i=1,...,m (x(i),y(i));i=1,...,m 被称为训练集。注意，符号中的上标$"(i)"$只是训练集中的一个索引，与幂运算无关。我们还将使用X表示输入值的空间，并使用Y表示输出值的空间。在此示例中，X = Y =ℝ。

为了更正式地描述监督学习问题，我们的目标是给定训练集，学习一个函数h：X→Y，以便h（x）是对应y值的“良好”预测因子。由于历史原因，此函数h称为假设。如图所示，该过程如下所示：

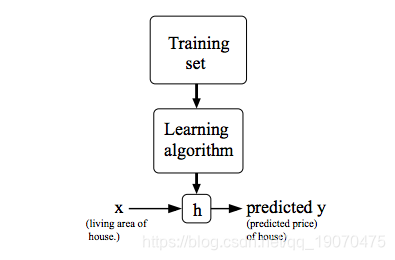
当我们要预测的目标变量是连续的时候，我们将学习问题称为回归问题。当y只能采用少量离散值时（例如，假设给定居住面积，我们想预测某个住宅是房子还是公寓），我们称其为分类问题。

成本函数

我们可以使用成本函数来衡量假设函数的准确性。这将假设的源于输入x的输出y和实际输出y的平均值进行平均差（实际上是平均值的简化形式）。
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( y ^ i − y i ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(\theta_0,\theta_1) = \frac{1}{2m} \sum_{i=1}^m(\hat{y}_i - y_i)^2= \frac{1}{2m} \sum_{i=1}^m(h_{\theta}(x_i) - y_i)^2 J(θ0​,θ1​)=2m1​i=1∑m​(y^​i​−yi​)2=2m1​i=1∑m​(hθ​(xi​)−yi​)2
h θ ( x i ) − y i h_\theta(x_i)-y_i hθ​(xi​)−yi​表示预测值与实际值的差值
此函数称为“平方误差函数”或“均方误差”。均值减半是为了方便计算梯度下降，因为平方函数的导数项将抵消二分之一，下图总结了成本函数的作用：

成本函数 Intuition I

如果我们尝试从视觉上考虑它，我们的训练数据集将散布在xy平面上。我们正在尝试画一条直线（定义为 h θ ( x ) h_\theta(x) hθ​(x)）使他能通过这些分散的数据点。

我们的目标是获得最可能的线。最佳可能的线应是这样，以使散射点与该线的平均垂直垂直距离最小。理想情况下，直线应穿过训练数据集的所有点。在这种情况下， J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0​,θ1​)将为0。以下示例显示了成本函数为0的理想情况。

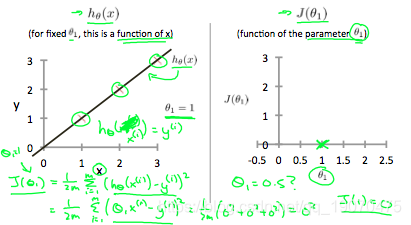
当 θ 1 = 1 \theta_1 = 1 θ1​=1，我们的模型中的每个数据点的斜率均为1。相反，当 θ 1 = 0.5 \theta_1 = 0.5 θ1​=0.5，我们看到从拟合到数据点的垂直距离增加了。

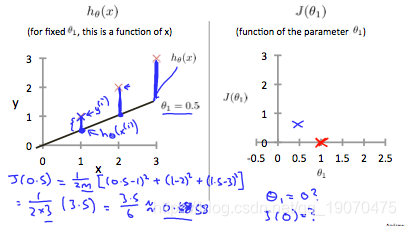
这将我们的成本函数提高到0.58。绘制其他几个点可得出下图：

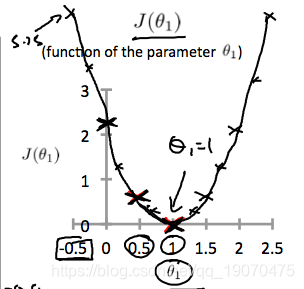
因此，作为目标，我们应尽量减少成本函数。在这种情况下， θ 1 = 1 \theta_1=1 θ1​=1是我们的全局最低要求。

成本函数 Intuition II

等高线图是包含许多等高线的图形。两个变量函数的轮廓线在同一条线的所有点上都具有恒定值。这种图的一个示例是下面的右图。

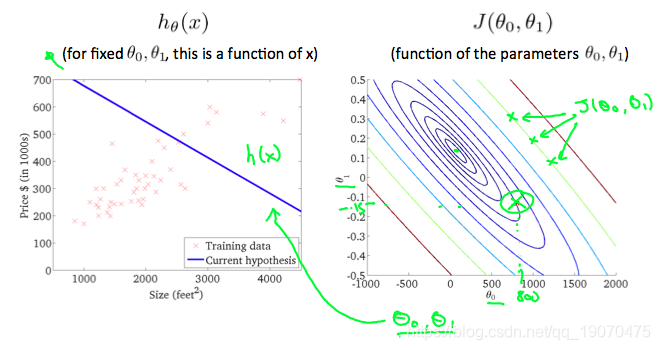
采用任何颜色并沿“圆”移动，人们都会期望获得与成本函数相同的值。例如，在上面的绿线上找到的三个绿点具有相同的值 J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0​,θ1​)结果，它们在同一行中被发现。带圆圈的x在出现以下情况时在左侧显示图形的成本函数的值 θ 0 = 800 和 θ 1 = − 0.15 \theta_0 = 800和\theta_1=-0.15 θ0​=800和θ1​=−0.15 ，取另一个h（x）并绘制其轮廓图，将得到以下图形：

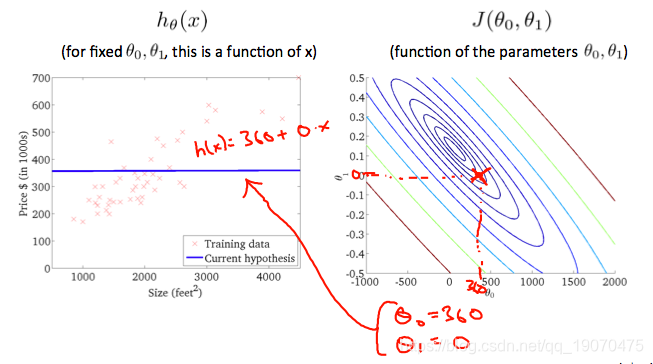
当 θ 0 = 360 a n d θ 1 = 0 \theta_0=360 and \theta_1 = 0 θ0​=360andθ1​=0时，值为 J ^ ( θ 0 , θ 1 ) \hat{J}(\theta_0,\theta_1) J^(θ0​,θ1​)，等高线图中的角点变得更靠近中心，从而减少了成本函数误差。现在给我们的假设函数一个稍微为正的斜率，可以更好地拟合数据。

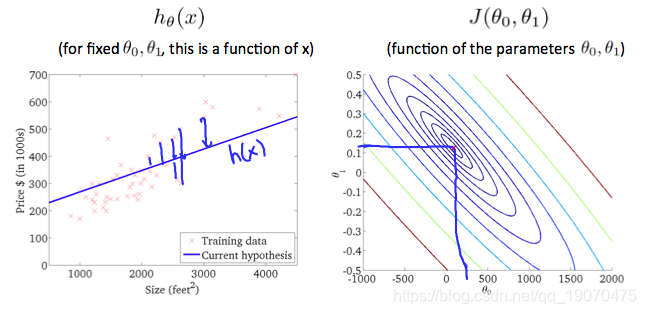
上图尽可能地使成本函数最小化，因此， θ 1 和 θ 0 \theta_1和\theta_0 θ1​和θ0​往往分别约为0.12和250。在我们的图上将这些值绘制在右侧似乎将我们的观点放在了最内层“圆”的中心。

梯度下降

因此，我们有了假设功能，并且有一种方法来衡量它与数据的拟合程度。现在我们需要估计假设函数中的参数，那就是梯度下降的方法。

想象一下，我们根据假设字段绘制假设函数图 θ 0 和 θ 1 \theta_0和\theta_1 θ0​和θ1​（实际上，我们将成本函数绘制为参数估计值的函数）。我们不是在绘制x和y本身的图，而是绘制假设函数的参数范围以及选择特定参数集所产生的成本。

我们把 θ 0 \theta_0 θ0​在x轴上， θ 1 \theta_1 θ1​在y轴上，垂直z轴上的成本函数。使用我们的假设和特定的theta参数，图上的点将是成本函数的结果。下图描述了这种设置。

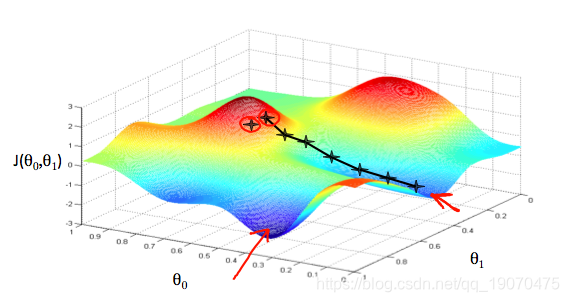
我们将知道，当成本函数位于图中凹坑的最底部时，即当其值最小时，我们就成功了。红色箭头显示图中的最小点。

我们这样做的方法是采用成本函数的导数（函数的切线）。切线的斜率是该点的导数，它将为我们提供一个方向。我们沿下降最陡的方向逐步降低成本函数。每个步骤的大小由参数α决定，称为学习率。

例如，上图中每个“星”之间的距离代表由我们的参数α确定的步长。较小的α将导致较小的步长，较大的α将导致较大的步长。步骤的执行方向由的偏导数确定 J ^ ( θ 0 , θ 1 ) \hat{J}(\theta_0,\theta_1) J^(θ0​,θ1​)。根据一个人在图上的起点，一个人可能会在不同的点结束。上图为我们提供了两个不同的起点，它们以两个不同的位置结束。

梯度下降算法为：

重复直到收敛：

θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_j := \theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1) θj​:=θj​−α∂θj​∂​J(θ0​,θ1​)
j = 0,1代表特征索引号。在每次迭代j时，应同时更新参数 θ 1 \theta_1 θ1​， θ 2 \theta_2 θ2​，…， θ n \theta_n θn​ 。特定参数之前先更新特定参数 J ( t h ) J^{(th)} J(th)的话，迭代将导致错误的实现。

梯度下降 Intuition

探讨了使用一个参数的情况 θ 1 \theta_1 θ1​并绘制其成本函数以实现梯度下降。我们的单个参数公式为：

重复直到收敛：
θ 1 : = θ 1 − α d d θ 1 J ( θ 1 ) \theta_1 := \theta_1-\alpha\frac{d}{d\theta_1}J(\theta_1) θ1​:=θ1​−αdθ1​d​J(θ1​)
不论坡度为 d d θ 1 J ^ ( θ 1 ) ， θ 1 \frac{d}{d\theta_1}\hat{J}(\theta_1)，\theta_1 dθ1​d​J^(θ1​)，θ1​最终收敛到其最小值。下图显示，当斜率为负时， θ 1 \theta_1 θ1​增加，当它为正数时， θ 1 \theta_1 θ1​减少。

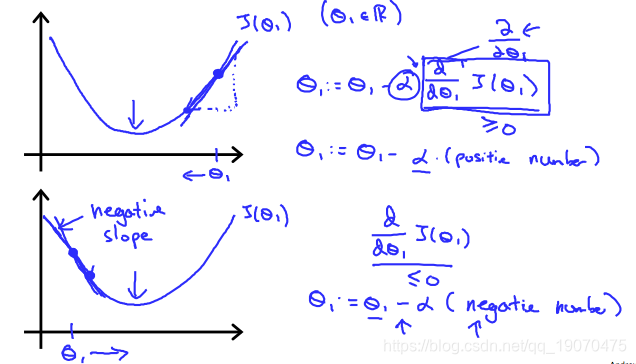
附带一提，我们应该调整参数 $\alpha$一种以确保梯度下降算法在合理的时间内收敛。未能收敛或没有太多时间获得最小值表示我们的步长是错误的。

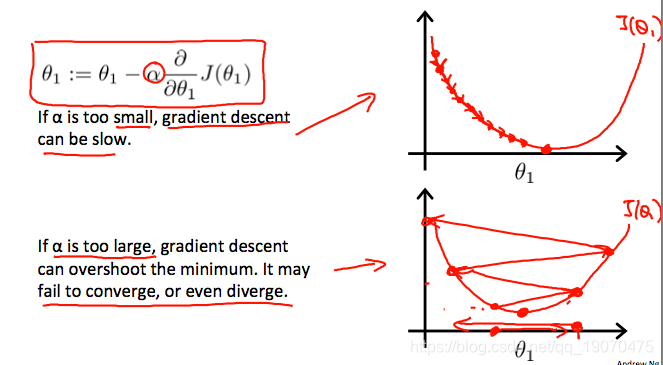
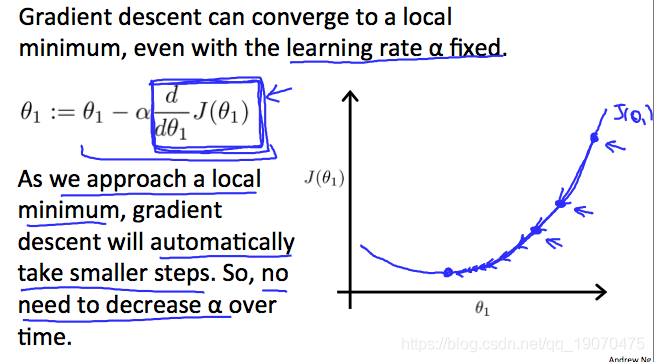
梯度下降如何以固定步长收敛 $\alpha$?
融合的直觉是 d d θ 1 J ( θ 1 ) \frac{d}{d\theta_1}J(\theta_1) dθ1​d​J(θ1​)当我们接近凸函数的底部时，接近0。至少，导数将始终为0，因此我们得到：
θ 1 : = θ 1 − α ∗ 0 \theta_1:=\theta_1-\alpha*0 θ1​:=θ1​−α∗0

线性回归的梯度下降

当专门用于线性回归时，可以得出新的形式的梯度下降方程。我们可以用实际成本函数和实际假设函数代替，并将等式修改为：
r e p e a t u n t i l c o n v e r g e n c e { θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x i ) − y i ) θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( ( h θ ( x i ) − y i ) x i ) } \begin{aligned} repeat\,until\,convergence \lbrace \newline \\ \theta_0 := \theta_0 - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x_i)-y_i) \newline \\ \theta_1:=\theta_1-\alpha\frac{1}{m}\sum_{i=1}^m((h_\theta(x_i)-y_i)x_i) \newline \\ \rbrace \end{aligned} repeatuntilconvergence{θ0​:=θ0​−αm1​i=1∑m​(hθ​(xi​)−yi​)θ1​:=θ1​−αm1​i=1∑m​((hθ​(xi​)−yi​)xi​)}​
其中m是训练集的大小， θ 0 \theta_0 θ0​一个常数，它将随着 θ 1 \theta_1 θ1​和 x i ， y i x_ {i}，y_ {i} xi​，yi​是给定训练集（数据）的值而改变。

请注意，我们将两种情况分开 θ j \theta_j θj​分成单独的方程式 θ 0 \theta_0 θ0​和 θ 1 \theta_1 θ1​而那 θ 1 \theta_1 θ1​我们正在繁殖 x i x_ {i} xi​最后由于导数。以下是推导的 ∂ ∂ θ j J ( θ ) \frac{\partial} {\partial \theta_j} J(\theta) ∂θj​∂​J(θ)仅举一个例子：
∂ ∂ θ j J ( θ ) = ∂ ∂ θ j 1 2 ( h θ ( x ) − y ) 2 = 2 ⋅ 1 2 ( h θ ( x ) − y ) ∂ ∂ θ j ( h θ ( x ) − y ) = ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( ∑ i = 0 n θ i x i − y ) = ( h θ ( x ) − y ) x j \begin{aligned} \frac{\partial}{\partial\theta_j}J(\theta) &=\frac{\partial}{\partial\theta_j}\frac{1}{2}(h_\theta(x)-y)^2 \\ &=2\cdot\frac{1}{2}(h_\theta(x)-y)\frac{\partial}{\partial\theta_j}(h_\theta(x)-y) \\ &= (h_\theta(x)-y)\cdot\frac{\partial}{\partial\theta_j}(\sum_{i=0}^n\theta_ix_i-y) \\ &= (h_\theta(x)-y)x_j \end{aligned} ∂θj​∂​J(θ)​=∂θj​∂​21​(hθ​(x)−y)2=2⋅21​(hθ​(x)−y)∂θj​∂​(hθ​(x)−y)=(hθ​(x)−y)⋅∂θj​∂​(i=0∑n​θi​xi​−y)=(hθ​(x)−y)xj​​
所有这些的要点是，如果我们从对假设的猜测开始，然后重复应用这些梯度下降方程，则我们的假设将变得越来越准确。

因此，这只是原始成本函数J的梯度下降。此方法着眼于每个步骤的整个训练集中的每个示例，称为批梯度下降。请注意，虽然梯度下降通常可能会受到局部极小值的影响，但我们在此处针对线性回归提出的优化问题只有一个全局最优，而没有其他局部最优。因此，梯度下降总是会收敛（假设学习率α不太大）到全局最小值。实际上，J是一个凸二次函数。这是梯度下降的示例，因为它可以使二次函数最小化。

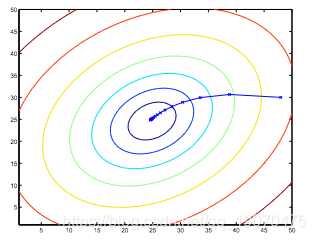
上面显示的椭圆是二次函数的轮廓。还显示了梯度下降所采取的轨迹，该轨迹在（48,30）处初始化。图中的x（用直线连接）标记了梯度下降收敛到最小值时经历的θ的连续值。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！