文章目录

• 地宫取宝
• • 1.普通递归暴力（拿50%的分）
  • 2.利用记忆型的递归（拿70%的分）
  • 3.DP(拿100%的分)

地宫取宝

问题描述　　
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。输入格式　　输入一行3个整数，用空格分开：n m k (1<=n,m<=50, 1<=k<=12)

接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值输出格式　　要求输出一个整数，表示正好取k个宝贝的行动方案数。该数字可能很大，输出它对 1000000007 取模的结果。样例输入2 2 2

1 2

2 1
样例输出
2

样例输入
2 3 2

1 2 3

2 1 5
样例输出
14

这一题是个dfs问题，把所有可能的结果都遍历过去，这一题的难点在很难拿到满分（性能上有些难以把控）下面是两种代码但是很可惜都没有拿到满分。

1.普通递归暴力（拿50%的分）

#include
using namespace std;
int n,m,k;
int ans;
int data[50][50];
void dfs(int x,int y,int maxtemp,int k1){if(x>=n||y>=m){//越界return;}if(k1>k){//宝物拿多了return ;}int value=data[x][y];//取当前位置宝物的价值//走到最后一个格子宝物数量正正好好够if(k1==k&&(x==n-1)&&(y==m-1)){ans++;return ;}//刚好处于最后一个格子且k1+1=k，data[x][y]>maxtemp那样就只能拿if(k1==k-1&&maxtemp<value&&(x==n-1)&&(y==m-1)){//这一点要特别注意k1=k-1ans++;return;}if(value>maxtemp){//当当前坐标的价值大于之前宝物的最大值时有4种选择dfs(x+1,y,value,k1+1);//拿走,向下走dfs(x+1,y,maxtemp,k1);//不拿走,向下走dfs(x,y+1,value,k1+1);//拿走,向右走dfs(x,y+1,maxtemp,k1);//不拿走,向右走}else{//value<=maxtemp时只有2种选择：向右和向下dfs(x,y+1,maxtemp,k1);dfs(x+1,y,maxtemp,k1);}
}int main(){cin>>n>>m>>k;for(int i=0;i<n;i++){for(int j=0;j<m;j++){cin>>data[i][j];}}int max=-1;dfs(0,0,max,0);cout<<ans<<endl;system("pause");//暂停观察结果return 0;
}

运行结果：

2.利用记忆型的递归（拿70%的分）

其实和普通递归差不多就是有了一个记忆的功能当踩到某个点时如果之前已经踩过了就直接用他的值就好了，不要重新计算，提高效率，对比普通递归需要改动的也只是在开头和结尾处

#include
#include
using namespace std;
int n,m,k;
int data[50][50];
long long test[50][50][14][13];//放访问过的元素----记忆 利用long long范围可以存点
long long dfs2(int x,int y,int maxtemp,int k1){//判断是否访问过if(test[x][y][maxtemp+1][k1]!=-1){return test[x][y][maxtemp+1][k1];}long long ans=0;if(x>=n||y>=m){return 0;}if(k1>k){return 0;}int value=data[x][y];if(k1==k&&(x==n-1)&&(y==m-1)){ans++;return ans;}if(k1==k-1&&maxtemp<value&&(x==n-1)&&(y==m-1)){ans++;return ans;}if(value>maxtemp){ans+=dfs2(x+1,y,value,k1+1);ans+=dfs2(x+1,y,maxtemp,k1);ans+=dfs2(x,y+1,value,k1+1);ans+=dfs2(x,y+1,maxtemp,k1);}else{ans+=dfs2(x,y+1,maxtemp,k1);ans+=dfs2(x+1,y,maxtemp,k1);}test[x][y][maxtemp+1][k1]=ans;return ans;
}
int main(){cin>>n>>m>>k;for(int i=0;i<n;i++){for(int j=0;j<m;j++){cin>>data[i][j];}}//全部赋初值-1memset(test,-1,sizeof(test));//别忘了加头文件cstringint max=-1;cout<<dfs2(0,0,max,0)<<endl;system("pause");//暂停观察结果return 0;
}

运行结果：

3.DP(拿100%的分)

利用状态表示以及状态计算来快速计算出结果，所谓状态表示按题义来设置，就像这一题，它的题义是问从起点到终点取到k件物品的所有方案的集合，我们就可以针对其题义来设置状态表示f[i][j][k][c]，对于一些注意的点都已经标注在图中了，有兴趣可以自己画画图加深一下理解

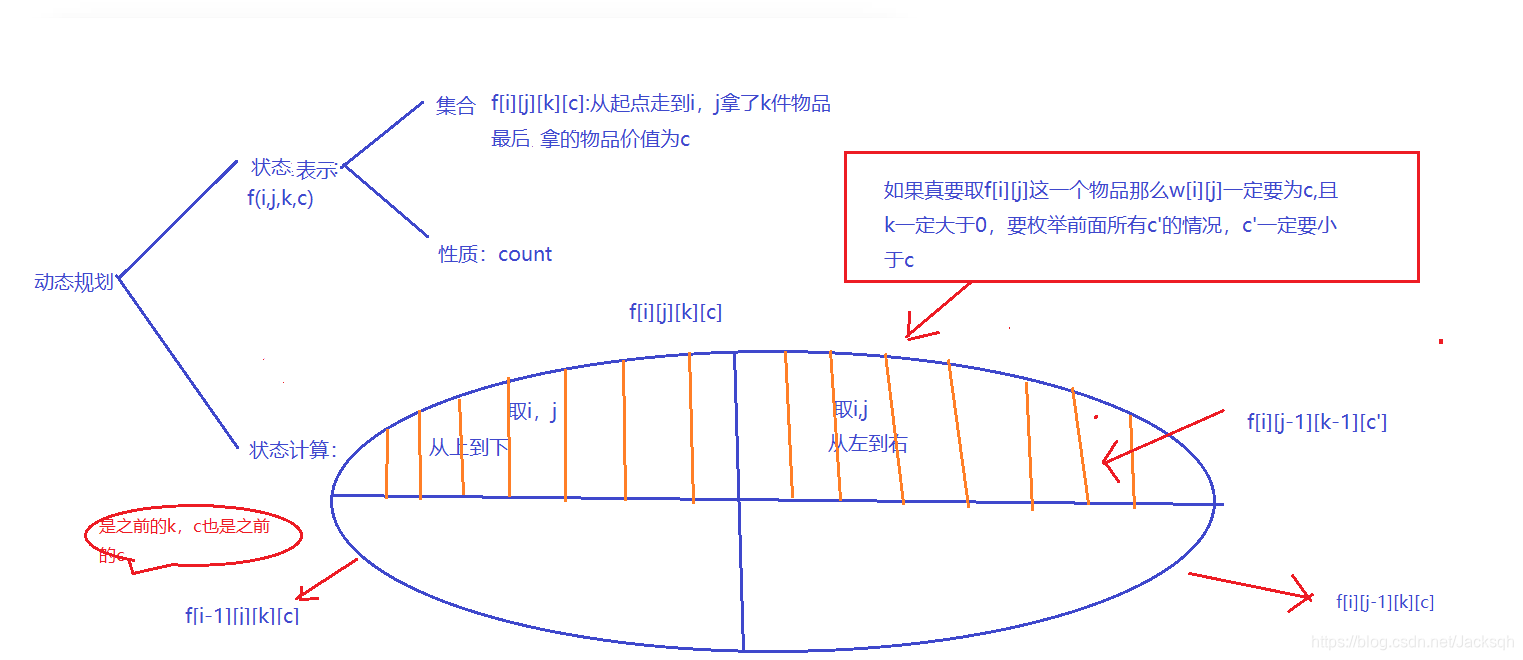
cpp:

#include
using namespace std;
const int N = 55;
const int MOD = 1000000007;
int w[N][N];
int f[N][N][13][14];
int n, m,k1;
int main() {cin >> n >> m >> k1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> w[i][j];w[i][j]++;//由于物品的价值可能会是0所以++}}/*原本应该是要为f[1][1][0][-1]=1但是数组下标不能为负数所以物品价值全部++，这样0就是最小值了*/f[1][1][0][0] = 1;//初始化f[1][1][1][w[1][1]] = 1;//初始化for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (i == 1 && j == 1)continue;for (int k = 0; k <= k1; k++) {for (int v = 0; v <= 13; v++) {int& tmp = f[i][j][k][v];tmp = (tmp + f[i - 1][j][k][v]) % MOD;tmp = (tmp + f[i][j-1][k][v]) % MOD;if(k>0&&w[i][j]==v)for (int c = 0; c < v; c++) {tmp = (tmp + f[i - 1][j][k-1][c]) % MOD;tmp = (tmp + f[i][j-1][k-1][c]) % MOD;}}}}}int res = 0;for (int i = 0; i <= 13; i++) {res= (res+f[n][m][k1][i])%MOD;}cout << res << endl;return 0;
}

运行结果：

注意：无论是状态的表示点还是最后的结果都要%MOD要不然会出错，而且MOD的时候最多两个相加就要MOD了，不能3个那样可能会爆
总结：在要利用递归的题目中如果要考虑效率的问题，以及在dfs时有交叉的情况时就可以采用记忆型的递归来提高效率，如果感觉前面两个都不行的话又涉及到取或不取的话就可以采用DP来做了，这次的地宫取宝是摘花生和最长上升子序列的组合题，用DP正好。做这种题目我一般都是先想暴力再试着优化

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！