【树模型与集成学习】(task7)XGBoost和LightGBM(更新ing)
学习总结
(1)XGBoost用二阶近似损失函数,LightGBM提出单边梯度采样和互斥特征绑定。
【打卡任务】侧边栏练习,知识回顾,实现回归问题下lightgbm的两个特性,即特征使用EFB预处理,节点分裂时按照xgboost分裂准则和单边梯度采样进行。
文章目录
- 学习总结
- 一、XGBoost算法
- 1.1 算法设计思路
- 1.2 梯度下降 and 二次函数近似
- (1)XGBoost的特值处理:
- (2)单个样本的损失函数
- 二、LightGBM算法
- (1)单边梯度采样 GOSS
- (2)互斥特征绑定 EFB
- 将互斥特征合并为单个特征
- 为什么互斥特征绑定问题与图着色问题等价?
- 三、作业
- 3.1 XGBoost和GBDT树有何异同?
- 3.2 叙述LightGBM中GOSS和EFB的作用及算法流程。
- Reference
一、XGBoost算法
回顾基础知识:

1.1 算法设计思路

由于树模型较强的拟合能力,需要对模型进行正则约束来控制每轮模型学习的进度,除了学习率参数之外,XGBoost还引入了两项作用于损失函数的正则项(控制模型的复杂度):
- 我们希望树的生长受到抑制而引入 γ T \gamma T γT,其中的 T T T为树的叶子节点个数, γ \gamma γ越大,树就越不容易生长;
- 接着我们希望模型每次的拟合值较小而引入 1 2 λ ∑ j = 1 T w j 2 \frac{1}{2}\lambda \sum_{j=1}^T w_j^2 21λj=1∑Twj2,其中的 w j w_j wj是回归树上第 i i i个叶子结点的预测目标值。
记第 m m m轮中第 i i i个样本在上一轮的预测值为 F i ( m − 1 ) F^{(m-1)}_i Fi(m−1),本轮需要学习的树模型为 h ( m ) h^{(m)} h(m),此时的损失函数即为
L ( m ) ( h ( m ) ) = γ T + 1 2 λ ∑ j = 1 T w j 2 + ∑ i = 1 N L ( y i , F i ( m − 1 ) + h ( m ) ( X i ) ) L^{(m)}(h^{(m)}) = \gamma T+\frac{1}{2}\lambda \sum_{j=1}^Tw_j^{2}+\sum_{i=1}^NL(y_i, F^{(m-1)}_i+h^{(m)}(X_i)) L(m)(h(m))=γT+21λj=1∑Twj2+i=1∑NL(yi,Fi(m−1)+h(m)(Xi))
从参数空间的角度而言,损失即为
L ( m ) ( F i ( m ) ) = γ T + 1 2 λ ∑ j = 1 T w j 2 + ∑ i = 1 N L ( y i , F i ( m ) ) L^{(m)}(F^{(m)}_i) = \gamma T+\frac{1}{2}\lambda \sum_{j=1}^Tw_j^{2}+\sum_{i=1}^NL(y_i, F^{(m)}_i) L(m)(Fi(m))=γT+21λj=1∑Twj2+i=1∑NL(yi,Fi(m))
不同于上一节中GBDT的梯度下降方法,XGBoost直接在 h ( m ) = 0 h^{(m)}=0 h(m)=0处(或 F i ( m ) = F i ( m − 1 ) F^{(m)}_i=F^{(m-1)}_i Fi(m)=Fi(m−1)处)将损失函数近似为一个二次函数,从而直接将该二次函数的顶点坐标作为 h ∗ ( m ) ( X i ) h^{*(m)}(X_i) h∗(m)(Xi)的值,即具有更小的损失。
1.2 梯度下降 and 二次函数近似
梯度下降法只依赖损失的一阶导数,当损失的一阶导数变化较大时,使用一步梯度获得的 h ∗ ( m ) h^{*(m)} h∗(m)估计很容易越过最优点,甚至使得损失变大(如子图2所示);

二次函数近似的方法(如上图的泰勒二次展开)需要同时利用一阶导数和二阶导数的信息,因此对于 h ∗ ( m ) h^{*(m)} h∗(m)的估计在某些情况下会比梯度下降法的估计值更加准确,或说对各类损失函数更有自适应性(如子图3和子图4所示)。
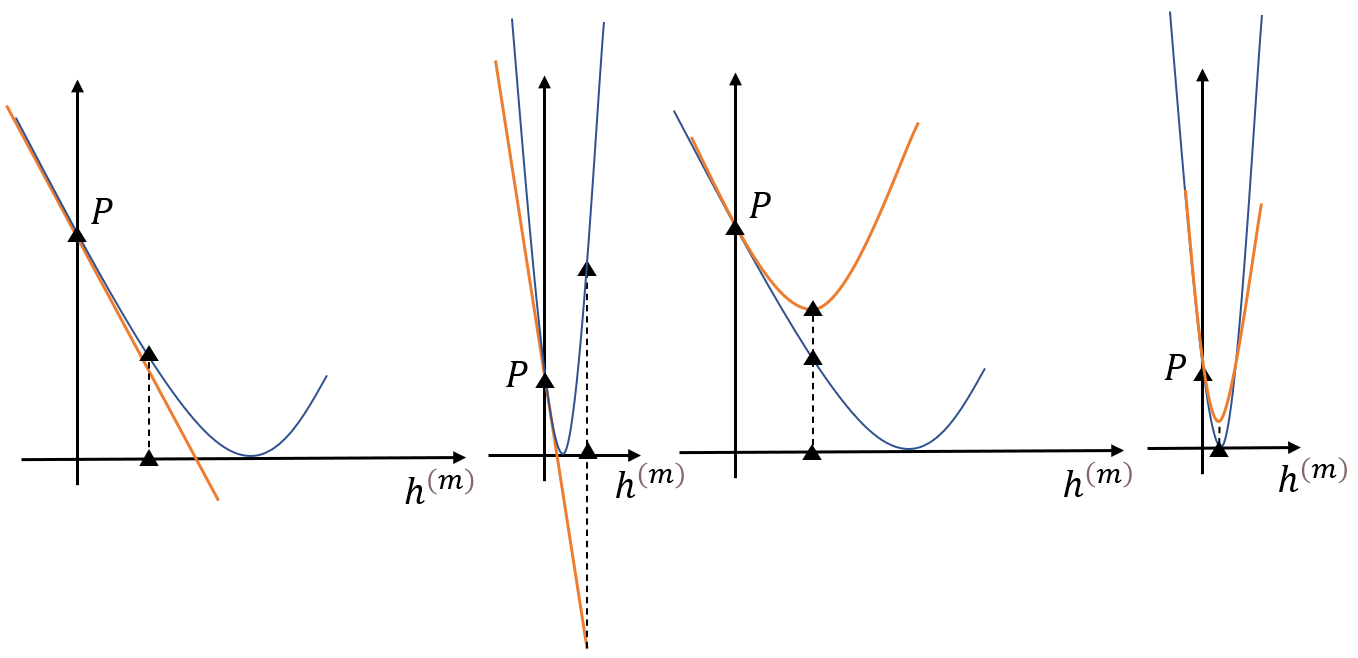
为了得到 h ∗ ( m ) ( X i ) h^{*(m)}(X_i) h∗(m)(Xi),记 h i = h ( m ) ( X i ) h_i=h^{(m)}(X_i) hi=h(m)(Xi), h = [ h 1 , . . . , h N ] \textbf{h}=[h_1,...,h_N] h=[h1,...,hN],我们需要先将损失函数显式地展开为一个关于 h ( m ) ( X i ) h^{(m)}(X_i) h(m)(Xi)的二次函数,:
L ( m ) ( h ) = γ T + 1 2 λ ∑ j = 1 T w j + ∑ i = 1 N L ( y i , F i ( m − 1 ) + h i ) ≈ γ T + 1 2 λ ∑ j = 1 T w j + ∑ i = 1 N [ L ( y i , F i ( m − 1 ) ) + ∂ L ∂ h i ∣ h i = 0 h i + 1 2 ∂ 2 L ∂ h i 2 ∣ h i = 0 h i 2 ] = γ T + 1 2 λ ∑ j = 1 T w j + ∑ i = 1 N [ ∂ L ∂ h i ∣ h i = 0 h i + 1 2 ∂ 2 L ∂ h i 2 ∣ h i = 0 h i 2 ] + c o n s t a n t \begin{aligned} L^{(m)}(\textbf{h}) &= \gamma T+\frac{1}{2}\lambda \sum_{j=1}^Tw_j+\sum_{i=1}^N L(y_i, F^{(m-1)}_i+h_i) \\ &\approx \gamma T+\frac{1}{2}\lambda \sum_{j=1}^Tw_j+\sum_{i=1}^N [L(y_i, F^{(m-1)}_i)+\left . \frac{\partial L}{\partial h_i}\right |_{h_i=0} h_i+\frac{1}{2}\left . \frac{\partial^2 L}{\partial h^2_i}\right |_{h_i=0} h^2_i]\\ &= \gamma T+\frac{1}{2}\lambda \sum_{j=1}^Tw_j+\sum_{i=1}^N [\left . \frac{\partial L}{\partial h_i}\right |_{h_i=0} h_i+\frac{1}{2}\left . \frac{\partial^2 L}{\partial h^2_i}\right |_{h_i=0} h^2_i] + constant \end{aligned} L(m)(h)=γT+21λj=1∑Twj+i=1∑NL(yi,Fi(m−1)+hi)≈γT+21λj=1∑Twj+i=1∑N[L(yi,Fi(m−1))+∂hi∂L∣∣∣∣hi=0hi+21∂hi2∂2L∣∣∣∣hi=0hi2]=γT+21λj=1∑Twj+i=1∑N[∂hi∂L∣∣∣∣hi=0hi+21∂hi2∂2L∣∣∣∣hi=0hi2]+constant
【练习】请写出 L ( m ) ( F i ( m ) ) L^{(m)}(F^{(m)}_i) L(m)(Fi(m))在 F i ( m ) = F i ( m − 1 ) F^{(m)}_i=F^{(m-1)}_i Fi(m)=Fi(m−1)处的二阶展开。
【练习】试说明不将损失函数展开至更高阶的原因。
【练习】请写出平方损失下的近似损失。
由于近似后损失的第二项是按照叶子结点的编号来加和的,而第三项是按照样本编号来加和的,我们为了方便处理,不妨统一将第三项按照叶子结点的编号重排以统一形式。设叶子节点 j j j上的样本编号集合为 I j I_j Ij,记 p i = ∂ L ∂ h i ∣ h i = 0 p_i=\left . \frac{\partial L}{\partial h_i}\right |_{h_i=0} pi=∂hi∂L∣∣∣hi=0且 q i = ∂ 2 L ∂ h i 2 ∣ h i = 0 q_i=\left . \frac{\partial^2 L}{\partial h^2_i}\right |_{h_i=0} qi=∂hi2∂2L∣∣∣hi=0,忽略常数项后有
L ~ ( m ) ( h ) = γ T + 1 2 λ ∑ j = 1 T w j + ∑ i = 1 N [ p i h i + 1 2 q i h i 2 ] = γ T + 1 2 λ ∑ j = 1 T w j + ∑ j = 1 T [ ( ∑ i ∈ I j p i ) w j + 1 2 ( ∑ i ∈ I j q i ) w i 2 ] = γ T + ∑ j = 1 T [ ( ∑ i ∈ I j p i ) w j + 1 2 ( ∑ i ∈ I j q i + λ ) w i 2 ] = L ~ ( m ) ( w ) \begin{aligned} \tilde{L}^{(m)}(\textbf{h}) &= \gamma T+\frac{1}{2}\lambda \sum_{j=1}^Tw_j+\sum_{i=1}^N [p_i h_i+\frac{1}{2}q_i h^2_i]\\ &= \gamma T+\frac{1}{2}\lambda \sum_{j=1}^Tw_j+\sum_{j=1}^T[(\sum_{i\in I_j} p_i )w_j+\frac{1}{2}(\sum_{i\in I_j}q_i )w^2_i]\\ &= \gamma T+\sum_{j=1}^T[(\sum_{i\in I_j} p_i )w_j+\frac{1}{2}(\sum_{i\in I_j}q_i +\lambda)w^2_i]\\ &=\tilde{L}^{(m)}(\textbf{w}) \end{aligned} L~(m)(h)=γT+21λj=1∑Twj+i=1∑N[pihi+21qihi2]=γT+21λj=1∑Twj+j=1∑T[(i∈Ij∑pi)wj+21(i∈Ij∑qi)wi2]=γT+j=1∑T[(i∈Ij∑pi)wj+21(i∈Ij∑qi+λ)wi2]=L~(m)(w)
上式的第二个等号是由于同一个叶子节点上的模型输出一定相同,即 I j I_j Ij中样本对应的 h i h_i hi一定都是 w j w_j wj。此时,我们将损失统一为了关于叶子节点值 w = [ w 1 , . . . , w T ] \textbf{w}=[w_1,...,w_T] w=[w1,...,wT]的二次函数,从而可以求得最优的输出值为
w j ∗ = − ∑ i ∈ I j p i ∑ i ∈ I j q i + λ w^*_j=-\frac{\sum_{i\in I_j}p_i}{\sum_{i\in I_j}q_i+\lambda} wj∗=−∑i∈Ijqi+λ∑i∈Ijpi
当前模型的近似损失(忽略常数项)即为
L ~ ( m ) ( w ∗ ) = γ T + ∑ j = 1 T [ − ( ∑ i ∈ I j p i ) 2 ∑ i ∈ I j q i + λ + 1 2 ( ∑ i ∈ I j p i ) 2 ∑ i ∈ I j q i + λ ] = γ T − 1 2 ∑ j = 1 T ( ∑ i ∈ I j p i ) 2 ∑ i ∈ I j q i + λ \begin{aligned} \tilde{L}^{(m)}(\textbf{w}^*)&=\gamma T+\sum_{j=1}^T[-\frac{(\sum_{i\in I_j}p_i)^2}{\sum_{i\in I_j}q_i+\lambda}+\frac{1}{2}\frac{(\sum_{i\in I_j}p_i)^2}{\sum_{i\in I_j}q_i+\lambda}]\\ &= \gamma T-\frac{1}{2}\sum_{j=1}^T\frac{(\sum_{i\in I_j}p_i)^2}{\sum_{i\in I_j}q_i+\lambda} \end{aligned} L~(m)(w∗)=γT+j=1∑T[−∑i∈Ijqi+λ(∑i∈Ijpi)2+21∑i∈Ijqi+λ(∑i∈Ijpi)2]=γT−21j=1∑T∑i∈Ijqi+λ(∑i∈Ijpi)2
在决策树的一节中,我们曾以信息增益作为节点分裂行为操作的依据,信息增益本质上就是一种损失,增益越大即子节点的平均纯度越高,从而损失就越小。因此我们可以直接将上述的近似损失来作为分裂的依据,即选择使得损失减少得最多的特征及其分割点来进行节点分裂。由于对于某一个节点而言,分裂前后整棵树的损失变化只和该节点 I I I及其左右子节点 I L I_L IL与 L R L_R LR的 w ∗ w^* w∗值有关,此时分裂带来的近似损失减少量为
G = [ γ T − 1 2 ( ∑ i ∈ I p i ) 2 ∑ i ∈ I q i + λ ] − [ γ ( T + 1 ) − 1 2 ( ∑ i ∈ I L p i ) 2 ∑ i ∈ I L q i + λ − 1 2 ( ∑ i ∈ I R p i ) 2 ∑ i ∈ I R q i + λ ] = 1 2 [ ( ∑ i ∈ I L p i ) 2 ∑ i ∈ I L q i + λ + ( ∑ i ∈ I R p i ) 2 ∑ i ∈ I R q i + λ − ( ∑ i ∈ I p i ) 2 ∑ i ∈ I q i + λ ] − γ \begin{aligned} G&= [\gamma T-\frac{1}{2}\frac{(\sum_{i\in I}p_i)^2}{\sum_{i\in I}q_i+\lambda}] - [\gamma (T+1)-\frac{1}{2}\frac{(\sum_{i\in I_L}p_i)^2}{\sum_{i\in I_L}q_i+\lambda}- \frac{1}{2}\frac{(\sum_{i\in I_R}p_i)^2}{\sum_{i\in I_R}q_i+\lambda}]\\ &= \frac{1}{2}[\frac{(\sum_{i\in I_L}p_i)^2}{\sum_{i\in I_L}q_i+\lambda}+\frac{(\sum_{i\in I_R}p_i)^2}{\sum_{i\in I_R}q_i+\lambda}-\frac{(\sum_{i\in I}p_i)^2}{\sum_{i\in I}q_i+\lambda}] -\gamma \end{aligned} G=[γT−21∑i∈Iqi+λ(∑i∈Ipi)2]−[γ(T+1)−21∑i∈ILqi+λ(∑i∈ILpi)2−21∑i∈IRqi+λ(∑i∈IRpi)2]=21[∑i∈ILqi+λ(∑i∈ILpi)2+∑i∈IRqi+λ(∑i∈IRpi)2−∑i∈Iqi+λ(∑i∈Ipi)2]−γ
模型应当选择使得 G G G达到最大的特征和分割点进行分裂。
(1)XGBoost的特值处理:
XGBoost不支持分类变量处理,此处的特值是指稀疏值和缺失值,它们的处理方式类似:把0值或缺失值固定,先统一划分至左侧子节点,遍历非0值或非缺失值分割点进行不纯度计算,再统一划分至右侧子节点,又进行非0值或非缺失值分割点的遍历计算,从而得到当前节点当前特征的稀疏值或缺失值默认分配方向以及最佳分割点。特别的是,当训练时特征没有遇到缺失值但预测值出现时,它将会被分配给子节点样本数较多的一侧。
【练习】在下列的三个损失函数 L ( y , y ^ ) L(y,\hat{y}) L(y,y^)中,请选出一个不应作为XGBoost损失的函数并说明理由。
- Root Absolute Error: ∣ y − y ^ ∣ \sqrt{\vert y-\hat{y}\vert} ∣y−y^∣
- Squared Log Error: 1 2 [ log ( y + 1 y ^ + 1 ) ] 2 \dfrac{1}{2}[\log(\dfrac{y+1}{\hat{y}+1})]^2 21[log(y^+1y+1)]2
- Pseudo Huber Error: δ 2 ( 1 + ( y − y ^ δ ) 2 − 1 ) \delta^2(\sqrt{1+(\dfrac{y-\hat{y}}{\delta})^2}-1) δ2(1+(δy−y^)2−1)
(2)单个样本的损失函数
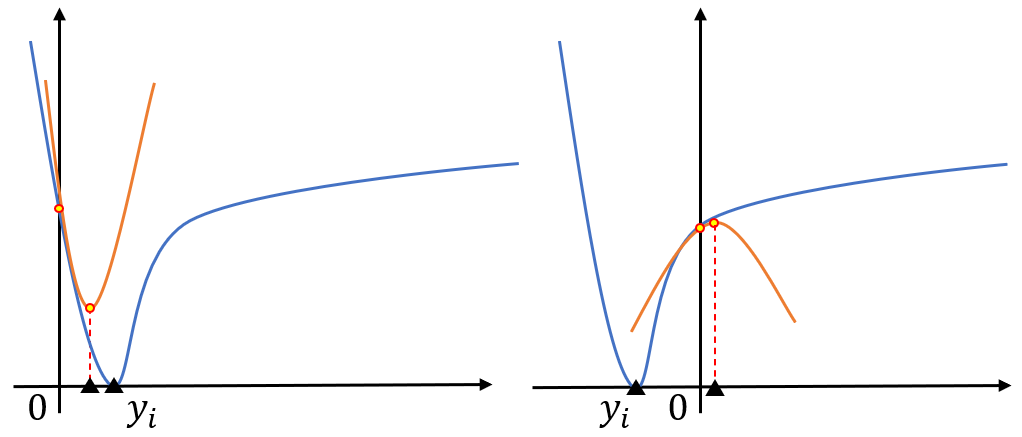
最后我们来重新回到单个样本的损失函数上:由于XGBoost使用的是二阶展开,为了保证函数在拐点处取到的是近似损失的最小值,需要满足二阶导数 q i > 0 q_i>0 qi>0。当损失函数不满足此条件时, h i ∗ h^*_i hi∗反而会使得损失上升,即如下图中右侧的情况所示,而使用梯度下降法时并不会产生此问题。因此,我们应当选择在整个定义域上或在 y i y_i yi临域上二阶导数恒正的损失函数,例如平方损失。
二、LightGBM算法
LightGBM的GBDT原理与XGBoost的二阶近似方法完全一致,并且在此基础上提出了两个新算法,它们分别是单边梯度采样(GOSS)以及互斥特征绑定(EFB)。
(1)单边梯度采样 GOSS
在GBDT中,计算出的梯度值绝对值越小则说明样本预测地越是准确,而梯度绝对值越大则说明样本预测的偏离程度越大,因此我们可以考虑对梯度绝对值小的样本进行抽样。
具体说,对样本梯度绝对值排序后,先选出Top a % a \% a%梯度绝对值对应的样本,再从剩下 ( 1 − a ) (1-a) (1−a)的样本中抽取 b % b \% b%的样本(此处 b % b\% b%是对于总样本的百分比)。此时,考虑基于均方损失的GBDT回归,记当前节点、左子节点、右子节点的梯度均值为 g ˉ , g ˉ L , g ˉ R \bar{g},\bar{g}_L,\bar{g}_R gˉ,gˉL,gˉR,设特征及其分割点为 F , d F,d F,d,原先的信息增益为
G a i n ( F , d ) = 1 N [ ∑ i = 1 N ( g i − g ˉ ) 2 − ∑ i = 1 N L ( g i ( L ) − g ˉ L ) 2 − ∑ i = 1 N R ( g i ( R ) − g ˉ R ) 2 ] = 1 N [ ( ∑ i = 1 N g i 2 − N g ˉ 2 ) − ( ∑ i = 1 N L g i ( L ) 2 − N g ˉ L 2 ) − ( ∑ i = 1 N R g i ( R ) 2 − N g ˉ R 2 ) ] ∝ 1 N [ ( ∑ i = 1 N L g i ( L ) ) 2 N L + ( ∑ i = 1 N R g i ( R ) ) 2 N R ] \begin{aligned} Gain(F,d) &= \frac{1}{N}[\sum_{i=1}^N(g_i-\bar{g})^2-\sum_{i=1}^{N_L}(g^{(L)}_i-\bar{g}_L)^2-\sum_{i=1}^{N_R}(g^{(R)}_i-\bar{g}_R)^2]\\ &= \frac{1}{N} [(\sum_{i=1}^Ng_i^2-N\bar{g}^2)-(\sum_{i=1}^{N_L}{g^{(L)}_i}^2-N{\bar{g}_L}^2)-(\sum_{i=1}^{N_R}{g^{(R)}_i}^2-N{\bar{g}_R}^2)] \\ &\propto \frac{1}{N}[\frac{(\sum_{i=1}^{N_L}{g^{(L)}_i})^2}{N_L}+\frac{(\sum_{i=1}^{N_R}{g^{(R)}_i})^2}{N_R}] \end{aligned} Gain(F,d)=N1[i=1∑N(gi−gˉ)2−i=1∑NL(gi(L)−gˉL)2−i=1∑NR(gi(R)−gˉR)2]=N1[(i=1∑Ngi2−Ngˉ2)−(i=1∑NLgi(L)2−NgˉL2)−(i=1∑NRgi(R)2−NgˉR2)]∝N1[NL(∑i=1NLgi(L))2+NR(∑i=1NRgi(R))2]
记划分到左子节点对应的a部分样本为 A L A_L AL、划分到左子节点对应的b部分抽样样本为 B L B_L BL、划分到右子节点对应的a部分样本为 A R A_R AR、划分到右子节点对应的b部分抽样样本为 B R B_R BR。
对于抽样部分的梯度和,我们使用 1 − a b \frac{1-a}{b} b1−a来进行补偿,例如原来从10个样本中划分6个为a部分,从剩下的4个中抽出两个为b部分,那么b部分的样本梯度和估计就是抽出两个样本的梯度和乘以 1 − 0.6 0.2 \frac{1-0.6}{0.2} 0.21−0.6。因此,可以写出对应的 G a i n ~ ( F , d ) \tilde{Gain}(F,d) Gain~(F,d)为
G a i n ~ ( F , d ) = 1 N [ ( ∑ i ∈ A L g i + 1 − a b ∑ i ∈ B L g i ) 2 N L + ( ∑ i ∈ A R g i + 1 − a b ∑ i ∈ B R g i ) 2 N R ] \tilde{Gain}(F,d) = \frac{1}{N}[\frac{(\sum_{i\in A_L}{g_i}+\frac{1-a}{b}\sum_{i\in B_L}{g_i})^2}{N_L}+\frac{(\sum_{i\in A_R}{g_i}+\frac{1-a}{b}\sum_{i\in B_R}{g_i})^2}{N_R}] Gain~(F,d)=N1[NL(∑i∈ALgi+b1−a∑i∈BLgi)2+NR(∑i∈ARgi+b1−a∑i∈BRgi)2]
(2)互斥特征绑定 EFB
实际的数据特征中可能有许多稀疏特征,即其非零值的数量远小于零值的数量,因此希望能够将这些特征进行合并来减少稀疏特征的数量,从而减少直方图构建的时间复杂度。
一族互斥特征:任意两个特征都不同时取非零值的特征集合;
数据集中的所有特征可被划分为这样的若干族互斥特征,例如下面就是一族互斥特征。
| 特征1 | 特征2 | 特征3 | |
|---|---|---|---|
| 样本1 | 0 | 1 | 0 |
| 样本2 | -1 | 0 | 0 |
| 样本3 | 0 | 0 | 0 |
【练习】请求出顶点最大度(即最多邻居数量)为 d d d的无向图在最差和最好情况下需要多少种着色数,同时请构造对应的例子。
【练习】在最差情况下LightGBM会生成几族互斥特征?这种情况的发生需要满足什么条件?
将互斥特征合并为单个特征
LightGBM提出了将互斥特征合并为单个特征的策略,从而让构建直方图的时间复杂度得以降低,因此需要找到最少的互斥绑定数量,即最少可以划分为几族。遗憾的是这个问题等价于图的着色问题,故它是NP-Hard的,目前并不存在多项式复杂度的解决方案,但我们可以通过近似方法来求解。
为什么互斥特征绑定问题与图着色问题等价?
如果我们把图的每一个顶点看做特征,将顶点之间是否存在边取决于两个特征是否存在同时为非零值的情况,若是则连接,那么此时没有边的顶点则代表他们之间满足互斥条件,将其涂上同种颜色作为同一族互斥特征,而寻找最少的绑定数量即是要寻找图的最少着色数。
下图展示了Petersen图最少需要三种着色数。

在实际操作中,由于严格互斥的特征数量可能还并不算多,但是几乎互斥的特征数量却很多,若存在一个样本使得两个特征同时为非零值则称它们存在一次冲突,所谓几乎互斥即一族特征之间的冲突总数不超过给定的最大冲突数 K K K,此时即使两个顶点之间存在边的连接,只要新加入的顶点能够使得这族特征满足几乎互斥的条件,那么就仍然可进行合并(或着相同颜色),如果此时新顶点与任意一族特征都不满足几乎互斥,那么将自身作为新的一族互斥特征集合的第一个元素(或着新的颜色)。
上述的讨论解决了特征绑定的问题,但我们只是将互斥特征放在了同一个集合里,还没有解决特征合并的问题。直观上说,我们需要用一个特征来表示多个特征时,要求新特征关于原特征族是可辨识的,即存在一一对应的关系。设需要合并的特征为 F 1 , . . . , F m F_1,...,F_m F1,...,Fm,它们对应的箱子分割点编号为 B i 1 , . . . , B i k i ( i = 1 , . . . , m ) B_{i1},...,B_{ik_i}(i=1,...,m) Bi1,...,Biki(i=1,...,m)。由稀疏性,这里假设 B i 1 B_{i1} Bi1是0对应的箱子。对于样本 s s s而言,如果其对应的特征都为0时,则投放至 B ~ 1 \tilde{B}_{1} B~1号,若第 i i i个特征非0,且其原特征对应的所在箱子为 B i j B_{ij} Bij,则投放至 B ~ k \tilde{B}_{k} B~k号,其中
k = j + ∑ p = 1 i − 1 k p k = j+ \sum_{p=1}^{i-1} k_p k=j+p=1∑i−1kp
对于上述的互斥特征绑定算法而言,我们确实能够对原数据集的特征进行互斥划分,也提取得到了新的直方图分割点,但考虑如下的情况:特征一和特征二是一族互斥特征,当遍历分割点位于特征一对应的非零区域时,此时右侧的点位对应所有的样本被划入右子节点,可此时划入右子节点的特征二非零值,由于互斥特性,本质上其特征一的值还是零,那么这种划分方法与不进行特征绑定单独考虑特征一相同位置的分割点,它们所计算出的信息增益值由于样本划分不同而会产生差异,这与论文中所描述的互斥特征绑定算法能够无损地提高性能不一致。
三、作业
3.1 XGBoost和GBDT树有何异同?
(可从目标损失、近似方法、分裂依据等方面考虑)
(1)GBDT是机器学习算法,XGBoost是该算法的工程实现。
(2)在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
(3)GBDT在模型训练时只使用了损失函数的一阶导数信息,XGBoost对损失函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
(4)传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类器,比如线性分类器。
(5)传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用与随机森林类似的策略,支持对数据进行采样。
(6)传统的GBDT没有对缺失值进行处理,XGBoost能够自动学习出缺失值的处理策略。
3.2 叙述LightGBM中GOSS和EFB的作用及算法流程。
Reference
(1)https://datawhalechina.github.io/machine-learning-toy-code/index.html
(2)《百面机器学习》
(3)《统计学习方法》李航
(4)官网:https://lightgbm.readthedocs.io/en/latest/
(5)深入理解XGBoost—英文课程
(6)梯度提升机(Gradient Boosting Machine)之 LightGBM
(7)不手写lightgbm(1)—怎么分桶的
(8)xgboost原理和应用分析
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!