2020九月十月暂记

Sept.&Oct.

• • • 新&重&难点：
    • 2020.9.4
    • 2020.9.9
    • 2020.9.30
    • 10.6模拟赛
    • 恶补状压DP
    • 10.23
    • 10.31

新&重&难点：

1. 状态压缩动态规划：(网格中)逐行状态转移 ;逐格状态转移(轮廓线优化)
2. 计算几何：扫描线(+线段树)；半平面交；曼哈顿距离与切比雪夫距离转换
3. 数学：二项式定理与二项式反演；概率期望；逆元求 t × a − 1 m o d b t\times a^{-1}\mod b t×a−1modb
4. 图论综合：最短路为主；(LCA、生成树、缩点……)
5. 数据结构综合：线段树为主
6. 大赛后希望学习：四边形不等式优化区间dp，斜率优化dp，强连通分量……更多学习计划写在11月暂记里吧。。。

2020.9.4

2020.9.4
T1
找出所有能到达蹦床的位置，将这些位置全部打上标记
如果当前出发点在能到达蹦床的位置，把打上标记的位置全部统计一遍
最后再找一段最大连续上升或最大连续下降序列并统计其中的楼房数便得到最后的答案
如果当前不在能到达蹦床的位置，统计从当前开始的一段最大连续上升或下降序列即为答案

#include
#include
#include
#includeusing namespace std;
int N,K,h[300005],jump[300005],ans,cnt,b[300005],sum[300005],tmp,lt,rt;
string s;
bool start; int main()
{cin>>N>>K;for(int i = 1;i <= N;i ++)cin>>h[i];cin>>s;for(int i = 0;i < s.size();i ++)if(s[i]=='T'){cnt++;jump[cnt] = i+1;}if(cnt != 0)//有蹦床的情况 {for(int i = 1;i <= cnt;i ++)//给能到蹦床上的区间打上标记 {if(b[jump[i]] != 0) continue;sum[i] = 1;b[jump[i]] = i;for(int j = jump[i] - 1 ;j >= 1;j --){if(h[j]>=h[j+1]&&b[j] == 0){b[j] = i,sum[i] ++;}else break;}	for(int j = jump[i] + 1;j <= N;j ++){if(h[j]>=h[j-1]&&b[j] == 0){b[j] = i,sum[i] ++;}else break;}}if(b[K]!=0)//当前可以到蹦床那么就可以把所有可到达蹦床区间的楼房都跳一遍 {tmp = 0;int maxn = -1;for(int i = 1;i <= cnt;i ++) ans += sum[i];if(b[N-1] == 0) tmp = 1;for(int i = N-1;i >= 1;i --){if(h[i]>=h[i+1] && b[i] == 0) tmp ++;else{maxn = max(maxn,tmp);tmp = 0;if(b[i] == 0) tmp ++;}}maxn = max(maxn,tmp);tmp = 0;if(b[N-1] == 0) tmp = 1;for(int i = N-1;i >= 1;i --){if(h[i]<=h[i+1] && b[i] == 0) tmp ++;else{maxn = max(maxn,tmp);tmp = 0;if(b[i] == 0) tmp ++;}}maxn = max(maxn,tmp);tmp = 0;if(b[1] == 0) tmp ++;for(int i = 2;i <= N;i ++){if(h[i]<=h[i-1] && b[i] == 0) tmp ++;else{maxn = max(maxn,tmp);tmp = 0;if(b[i] == 0) tmp ++;}}maxn = max(maxn,tmp);tmp = 0;if(b[1] == 0) tmp ++;for(int i = 2;i <= N;i ++){if(h[i]>=h[i-1] && b[i] == 0) tmp ++;else{maxn = max(maxn,tmp);tmp = 0;if(b[i] == 0) tmp ++;}}maxn = max(maxn,tmp);ans = maxn + ans;cout << ans << endl;return 0;}}//没有蹦床或是当前无法去到任何一个蹦床//统计楼房高度相平横向跳跃的总数 lt = rt = K;for(int i = K-1;i >= 1;i --)if(h[i] != h[i+1]){lt = i + 1;break;}for(int i = K+1;i <= N;i ++)if(h[i] != h[i-1]){rt = i - 1;break;}////tmp = 0;for(int i = lt-1;i >= 1;i --){if(h[i]<=h[i+1]) tmp ++;else{ans = max(ans,tmp);break;}}ans = max(ans,tmp);tmp = 0;for(int i = rt+1;i <= N;i ++){if(h[i]<=h[i-1]) tmp ++;else{ans = max(ans,tmp);break;}}ans = max(ans,tmp);ans += rt - lt + 1;cout << ans << endl;return 0;
}
/*
10 1
10 7 3 1 1 9 8 2 4 10
..T..T.T..
*/

2020.9.9

2020.9.9

• 收录整理

T2

2020.9.30

2020.9.30
T1

• 收录整理

当所有字符串变换成使得它们的公共前缀最长时，trie树的结点树最少
看到数据范围$1\le n\le 16$，自然先想到状压DP
由于字符串可以任意变换，只需统计字符串中每一种字母出现的个数就可以方便表示字符串，且方便接下来的操作
设$S$表示被选取加入trie树的字符串的集合， S ′ ⊆ S S'\subseteq S S′⊆S，$f(S)$表示在状态$S$下trie树的最少结点数，$p(S)$表示在$S$状态下，最大公共前缀的长度
则有： f ( S ) = f ( S ′ ) + f ( S − S ′ ) − p ( S ) f(S) = f(S')+f(S-S')-p(S) f(S)=f(S′)+f(S−S′)−p(S)

#include
#include
#include
#include
#includeusing namespace std;
const int inf = 0xfffffff;
int n,f[65540],tmp,tot,cnt[65540][30];
string s[25];int main()
{
//	freopen("test.txt","r",stdin);cin >> n;tot = (1<<n)-1;for(int i = 0; i <= tot;i ++) f[i] = inf;for(int i = 0;i <= tot;i ++)for(int j = 0;j < 26;j ++)cnt[i][j] = inf ;for(int i = 1;i <= n;i ++){cin >> s[i];tmp = 1<<(i-1);f[tmp] = s[i].size();for(int j = 0;j < 26;j ++) cnt[tmp][j] = 0;for(int j = 0;j < s[i].size();j ++) cnt[tmp][s[i][j]-'a'] ++;} f[0] = 0;for(int i = 1;i <= tot;i ++){tmp = 0;for(int j = 1;j <= n;j ++)if(((1<<(j-1))&i) > 0)for(int k = 0;k < 26;k ++)cnt[i][k] = min(cnt[i][k],cnt[(1<<(j-1))][k]);for(int k = 0;k < 26;k ++)tmp += cnt[i][k];for(int j = i&(i-1);j;j = (j-1)&i){int k = i - j;f[i] = min(f[i],f[k]+f[j]-tmp);}}cout << f[tot]+1 << endl;return 0;
}

T2

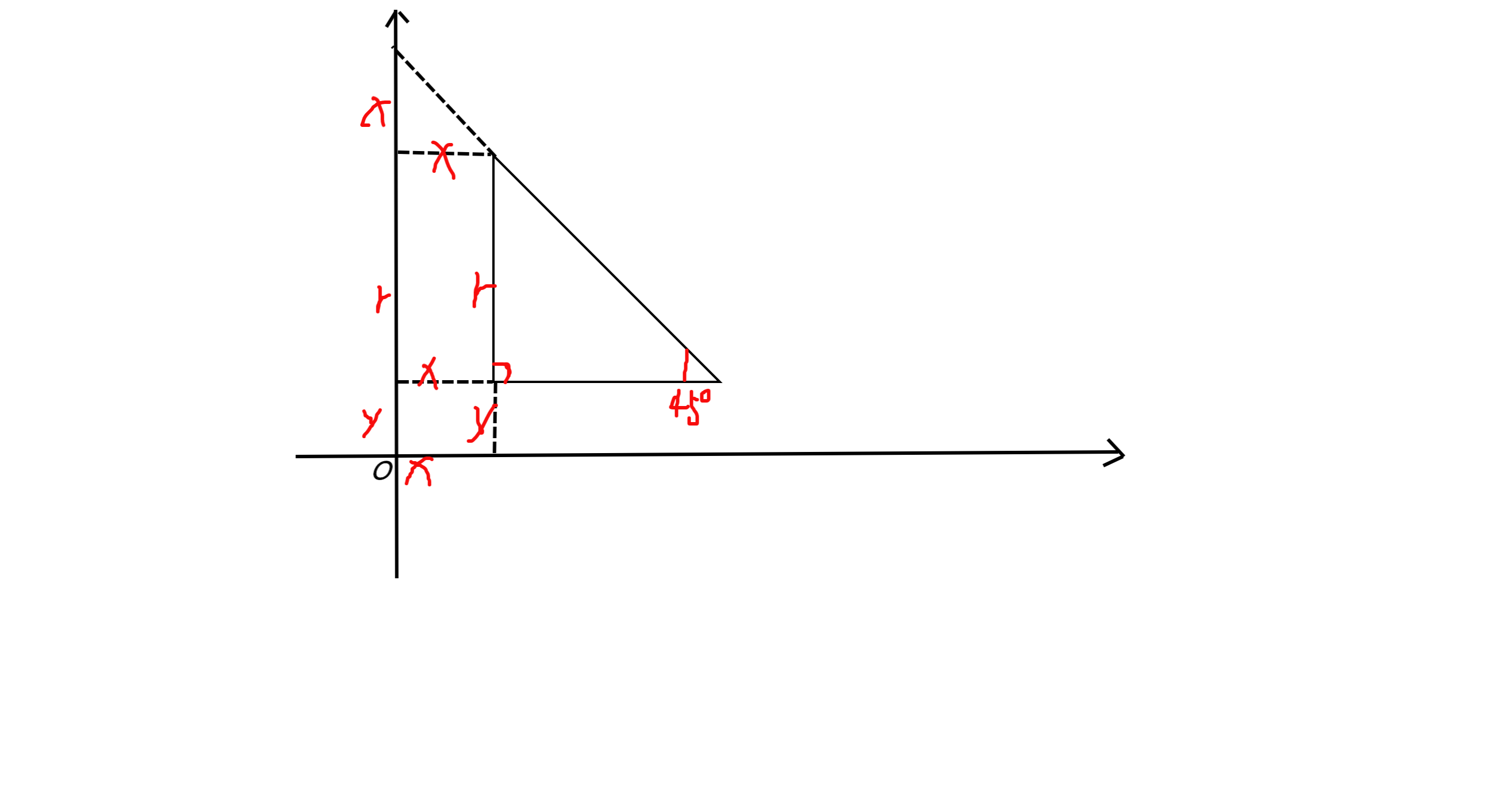
斜边所在直线$y=-x+b$由图中显然可知： y = − x + x ′ + y ′ + r ′ y = -x+x'+y'+r' y=−x+x′+y′+r′
故求两斜边中较下的一条，比较$b$即 x ′ + y ′ + r ′ x'+y'+r' x′+y′+r′即可

/*||\x  |__\+  | x |\r  |   |  \ +  |___|____\y  |_y_|__________*/
#include
#include
#include
#includeusing namespace std;
const long long inf = 0xfffffffff;
int n,tot,cnt,times[1105];
long long nx,ny,nc,x[1105],y[1105],c[1105];
double ans;int main()
{cin >> n;tot = (1<<n)-1;for(int i = 1;i <= n;i ++)cin >> x[i] >> y[i] >> c[i];for(int i = 1;i <= tot;i ++){cnt = 0;nc = inf;nx = -inf;ny = -inf;for(int j = 1;j <= n;j ++)if(((1<<(j-1))&i) > 0){nc = min(nc,x[j]+y[j]+c[j]);nx = max(nx,x[j]);ny = max(ny,y[j]);cnt ++;}ans += pow(-2,cnt-1)*max((long long)0,nc-nx-ny)*max((long long)0,nc-nx-ny)*0.5;}printf("%.1lf",ans);return 0;
} 

10.6模拟赛

• 收录整理
  
  又是状压DP

#include
#includeusing namespace std;
const int modnum = 1000000007;
int n,m,k,tot,s1;
int u[505],v[505],tmp;
bool map[30][30];
long long f[35][1048580],ans;int main()
{scanf("%d%d%d",&n,&m,&k);tot = (1 << n) - 1;for(int i = 1;i <= m;i ++){scanf("%d%d",&u[i],&v[i]);map[u[i]][v[i]] = 1;}f[0][0] = 1;for(int s = 1; s <= tot; s ++)//enumerate all the statesfor(int i = 1;i <= n;i ++)//enumerate the last number in this sequence{tmp = 0;if(((1<<(i-1))&s) > 0){s1 = s - (1<<(i-1));for(int j = 1;j <= n;j ++)if(((1<<(j-1))&s1) > 0){if(map[i][j]) tmp ++;//if the last number is i , it will cause tmp arguementsif(tmp > k) break;}if(tmp > k) continue;for(int j = 0;j <= (k-tmp);j ++)//enumerate last statusf[tmp+j][s] = (f[tmp+j][s]%modnum + f[j][s1]%modnum)%modnum;}}for(int i = 0;i <= k;i ++)//sum up the answerans = (ans%modnum + f[i][tot]%modnum)%modnum;printf("%lld",(ans%modnum));return 0;
}

恶补状压DP

• 收录整理
  状态压缩动态规划习题

T1

#include
#include
#includeusing namespace std;
const int modnum = 100000000;
int n,m,map[20][20],f[20][20][32780];
int st[20];
bool vis[20][20][32780];int dfs(int i,int j,int s)
{if(i>n) return 1;//全部放置完毕,算作一种方案 if(j>m) return dfs(i+1,1,s&st[i+1])%modnum;//this row has been counted,go to the next gridif(vis[i][j][s]) return f[i][j][s]%modnum;//we've known the answer and return itvis[i][j][s] = 1;//int now = 1<<(j-1);//the status of (i,j)if((s&now)==0)//we can't place a plant here{int s1 = (s|now);//we can't place a plant on (i,j) , but we can place a plant on (i+1,j)f[i][j][s] = dfs(i,j+1,s1)%modnum;//go to the next gridreturn f[i][j][s]%modnum;}int tmp = dfs(i,j+1,s)%modnum;//we don't place a plant hereint s2 = s - now;int next = 1<<j;//if we place a plant here,we can't place a plant on the next gridif(((next&s2)>0)&&(j<m)) s2 -= next;//figure out the status of placing a plant hereint tmp2 = dfs(i,j+1,s2)%modnum;//go to the next gridf[i][j][s] = (tmp+tmp2)%modnum;//sum up the answer
//	cout << i << ',' << j << ':' << s << " plant" << tmp << " empty" << tmp2 << endl;return f[i][j][s];
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) st[i]=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&map[i][j]);if(map[i][j])st[i]+=pow(map[i][j]*2,j-1);}}printf("%d",dfs(1,1,st[1])%modnum);return 0;
}

T2

#include
#include
#includeusing namespace std;
int n,map[15][15];
int f[2048],tot;int main()
{while(1){scanf("%d",&n);if(n == 0) break;tot = (1<<n) - 1;for(int i = 1;i <= n;i ++)for(int j = 1;j <= n;j ++)scanf("%d",&map[i][j]);for(int i = 0;i <= tot;i ++) f[i] = 0;for(int k = 1;k <= tot;k ++)for(int i = 0;i < n;i ++){int s1 = 1<<i;if((s1&k)>0)for(int j = i + 1;j < n;j ++){int s2 = 1<<j;if((s2&k)>0){int s3 = k - s1;int s4 = k - s2;f[k] = max(f[k],f[s3] + map[j+1][i+1]);f[k] = max(f[k],f[s4] + map[i+1][j+1]);}}}printf("%d\n",f[tot]);}return 0;
}

T3
T4

#include
#include
#include
#include
#includeusing namespace std;
const long long inf = 0xfffffffff;
typedef long long ll;
ll n,m,t,d[55][55],dis[55][55],f[66000][25];
int map[55][55],kx,ky,qx,qy,gx[55],gy[55],cnt,s1,ans,tot,num1;
int mark[55][55],nowx,nowy,nx,ny,dx[5] = {0,0,0,1,-1},dy[5] = {0,1,-1,0,0};
bool vis[55][55];
string s;int cnt1(int x)
{int tmp = 0;for(int i = 1;i <= cnt;i ++)if((x&(1<<(i-1))) > 0)tmp ++;return tmp;
}void bfs(int sx,int sy)
{memset(vis,0,sizeof(vis));for(int i = 1;i <= n;i ++)for(int j = 1;j <= m;j ++)d[i][j] = inf;queue< pair<int , int > > q;vis[sx][sy] = 1;d[sx][sy] = 0;q.push(make_pair(sx,sy));while(!q.empty()){nowx = q.front().first;nowy = q.front().second;q.pop();vis[nowx][nowy] = 0;for(int i = 1;i <= 4;i ++){nx = nowx + dx[i];ny = nowy + dy[i];if(nx > 0 && nx <= n && ny > 0 && ny <= m )if(d[nx][ny] > d[nowx][nowy] + 1 && map[nx][ny] == 1){d[nx][ny] = d[nowx][nowy] + 1;if(!vis[nx][ny]){vis[nx][ny] = 1;q.push(make_pair(nx,ny));}}}}for(int i = 0;i <= cnt + 1;i ++)dis[mark[sx][sy]][i] = d[gx[i]][gy[i]];return ;
}int main()
{memset(mark,128,sizeof(mark));//read datascanf("%lld%lld%lld",&n,&m,&t);for(int i = 1;i <= n;i ++){cin >> s;for(int j = 0;j < s.size();j ++){switch(s[j]){case '.':map[i][j+1] = 1;break;case '#':map[i][j+1] = 0;break;case 'G':cnt ++;gx[cnt] = i;gy[cnt] = j + 1;mark[i][j+1] = cnt;map[i][j+1] = 1;break;case 'K':kx = i;ky = j + 1;map[i][j+1] = 1;break;case 'Q':qx = i;qy = j + 1;map[i][j+1] = 1;break;}}}mark[kx][ky] = 0;mark[qx][qy] = cnt + 1;gx[0] = kx;gy[0] = ky;gx[cnt + 1] = qx;gy[cnt + 1] = qy;for(int i = 0;i <= cnt+1;i ++)for(int j = 0;j <= cnt + 1;j ++)dis[i][j] = inf;for(int i = 0;i <= cnt + 1;i ++)bfs(gx[i],gy[i]);tot = 1<<(cnt+1) - 1;for(int i = 0;i <= tot;i ++)for(int j = 0;j <= cnt+1; j ++)f[i][j] = inf;for(int i = 1;i <= cnt;i ++)f[(1<<(i-1))][i] = dis[0][i];for(int s = 0;s <= tot; s ++){num1 = cnt1(s);for(int i = 1;i <= cnt;i ++)if((s&(1<<(i-1))) > 0){s1 = s - (1<<(i-1));for(int j = 1;j <= cnt;j ++)if((s1&(1<<(j-1))) > 0)f[s][i] = min(f[s][i],f[s1][j]+dis[j][i]*num1);}}for(int s = 0;s <= tot;s ++){num1 = cnt1(s);for(int i = 1;i <= cnt;i ++)if((s&(1<<(i-1))) > 0){ll sum = f[s][i] + dis[i][cnt+1]*(num1+1);if(sum <= t)ans = max(ans,num1);}}printf("%d",ans);return 0;
}

T5

#include
#include
#include
#include
#includeusing namespace std;
const int inf = 2139062143;
int n,cp,k,r,u,v,cnt,f[45][1050],tot,tmp,s1,num;
int map[15][45][45],p[15][45],d[50];
bool vis[50];int cnt1(int x)
{int tmp = 0;for(int i = 1;i <= cp;i ++)if((x&(1<<(i-1))) > 0)tmp ++;return tmp;
}void dfs(int c,int now,int fa)
{if(vis[now]) return ;vis[now] = 1;for(int i = 1;i <= n;i ++)if(map[c][now][i]){map[c][fa][i] = 1;dfs(c,i,fa);}
}void solve()
{//initmemset(d,127,sizeof(d));memset(f,127,sizeof(f));memset(map,0,sizeof(map));memset(p,0,sizeof(p));//readscanf("%d%d",&n,&cp);for(int i = 1;i <= cp;i ++){scanf("%d",&k);for(int j = 1;j <= k;j ++){scanf("%d%d",&u,&v);map[i][u][v] = 1;}}for(int i = 0;i < n;i ++)for(int j = 1;j <= cp;j ++)scanf("%d",&p[j][i]);//dptot = 1<<(cp+1) - 1;for(int i = 0;i <= tot;i ++){num = cnt1(i);if(num > 3) continue;tmp = 0 ;for(int j = 1;j <= cp;j ++)if((i&(1<<(j-1))) > 0)tmp += p[j][0];f[0][i] = tmp;}memset(vis,0,sizeof(vis));queue<int > q; q.push(0);while(!q.empty()){int i = q.front();q.pop();vis[i] = 0;for(int s = 0;s <= tot;s ++)//enumrate the status of tickets{num = cnt1(s);if(num > 3) continue;for(int j = 1;j <= cp;j ++)//We buy tickets on this islandif((s&(1<<(j-1))) > 0){s1 = s - (1<<(j-1));f[i][s] = min(f[i][s],f[i][s1]+p[j][i]);}for(int j = 1;j <= cp;j ++)//We have bought tickets on other islandif((s&(1<<(j-1))) > 0){s1 = s - (1<<(j-1));for(int k = 0;k < n;k ++)if(map[j][i][k])//Use this ticket to travel from i to k{d[k] = min(d[k],f[i][s]);//update the minimum distanceif(f[k][s1] > f[i][s])//update the next status{f[k][s1] = f[i][s];if(!vis[k]){vis[k] = 1;q.push(k);//keep updating}}}}}}for(int i = 1;i < n;i ++){if(d[i] == inf) printf("-1 ");else printf("%d ",d[i]);}printf("\n");
}int main()
{scanf("%d",&r);for(int i = 1;i <= r;i ++)solve();return 0;
}

T6

#include
#include
#include
#includeusing namespace std;
int h,w,tot;
long long f[25][25][30000];
bool vis[25][25][30000];long long dfs(int x,int y,int s)
{if(x > h) return 1;//this rectangle is full of bricks if(y > w) return dfs(x+1,1,s);//next rowif(vis[x][y][s]) return f[x][y][s];vis[x][y][s] = 1;int s1 = 1<<(y-1);if((s1&s)>0) //the current grid is occupied by a vertical brick{f[x][y][s] = dfs(x,y+1,s-s1);// As for the next row,it won't be affected by this vertical brick return f[x][y][s];}long long tmp1 = 0;if(x < h)//place a vertical brick on this gridtmp1 = dfs(x,y+1,s1+s);//the placement of this brick will influence the way of placing bricks on the next rowint s2 = 1<<y;long long tmp2 = 0;if(y < w)//place a transverse brick on this gridif((s2&s)==0)//to check whether we can place this transverse brick or nottmp2 = dfs(x,y+1,s+s2);f[x][y][s] = tmp1 + tmp2;return f[x][y][s];
}int main()
{while(1){cin>>h>>w;if(h == 0 && w == 0) break;tot = (1<<(w+1))-1;memset(f,0,sizeof(f));memset(vis,0,sizeof(vis));cout << dfs(1,1,0) << endl;}return 0;
}

T7

#include
#include
#include
#includeusing namespace std;
const int inf = 2139062143;
int n,m,f[15][1050],tmp,tmp1,ans = inf,tot,b[15];
//1 refers to drawing vertically and 0 refers to drawing transversely
//regard # as 0 
bool map[15][15],flag;
string s;bool check(int now,int x)//the position of # in the map can't be 1 in the status
{if((b[now]&x) > 0) return 0;else return 1;
}int main()
{memset(f,127,sizeof(f));scanf("%d%d",&n,&m);for(int i = 1;i <= n;i ++){cin >> s;for(int j = 0;j < s.size();j ++)if(s[j] == '#'){map[i][j+1] = 1;b[i] += (1<<j);//record the status}}tot = 1<<(m+1) - 1;for(int s = 0;s <= tot; s++)//initalization{if(!check(1,s)) continue;flag = 0;tmp = 0;for(int j = 1;j <= m;j ++){if((s&(1<<(j-1))) > 0)//draw vertically{tmp ++;flag = 0;}else{if(map[1][j]){flag = 0;continue;}//draw transeverselyif(flag) continue;//draw with one stroke else{flag = 1;tmp ++;}}}f[1][s] = tmp;if(1 == n) ans = min(ans,f[1][s]);}for(int i = 2;i <= n;i ++){for(int s = 0;s <= tot;s ++)//the status of last row{if(!check(i-1,s)) continue;for(int s1 = 0;s1 <= tot;s1 ++)//the status of this row{if(!check(i,s1)) continue;flag = 0;tmp = 0;tmp1 = 0;for(int j = 1;j <= m;j ++){if((s1&(1<<(j-1))) > 0){flag = 0;//draw transeversely on the last rowif((s&(1<<(j-1))) == 0) tmp1 ++;//draw vertically this row}else{if(map[i][j]){flag = 0;continue;}if(flag) continue;else flag = 1,tmp ++;}}f[i][s1] = min(f[i][s1],f[i-1][s] + tmp1 + tmp);
//				cout << i << ' ' << s1 << ' ' << f[i][s1] << endl;if(i == n) ans = min(ans,f[i][s1]);}}}if(ans == inf) printf("0");else printf("%d",ans);return 0;
}

10.23

10.23模拟赛

T1
通过探索规律可以发现：只要算出2天内团伙的发展情况，此后的发展情况全部都由$t=0$，$t=1$，$t=2$的发展情况表示
我们可以算出：
t = 0 , f ( 0 ) = B t = 1 , f ( 1 ) = SSB t = 2 , f ( 2 ) = BBSSB \begin{array}{crl} t=0,f(0) = & \text {B}\\ t=1,f(1)= &\text {SSB} \\ t=2, f(2)= &\text {BBSSB} \\ \end{array} t=0,f(0)=t=1,f(1)=t=2,f(2)=​BSSBBBSSB​
再推几个式子发现：
t = 3 , f ( 3 ) = SSBSSBBBSSB t = 4 , f ( 4 ) = BBSSBBBSSBSSBSSBBBSSB ∵ f ( 3 ) = f ( 1 ) + f ( 1 ) + f ( 0 ) + f ( 0 ) + f ( 1 ) f ( 4 ) = f ( 2 ) + f ( 2 ) + f ( 1 ) + f ( 1 ) + f ( 2 ) ∴ 可 推 广 得 : f ( i ) = { B , i = 0 S S B , i = 1 B B S S B , i = 2 f ( i − 2 ) + f ( i − 2 ) + f ( i − 1 ) + f ( i − 1 ) + f ( i − 2 ) , i > 2 \begin{array}{crl} t=3, f(3) = & \text {SSBSSBBBSSB} \\ t=4, f(4) = & \text {BBSSBBBSSBSSBSSBBBSSB}\\ \end{array}\\ \begin{array}{l} \because \\ f(3) = f(1)+f(1)+f(0)+f(0)+f(1)\\ f(4)=f(2)+f(2)+f(1)+f(1)+f(2) \\ \therefore可推广得:\\ f(i) = \begin{cases} B &,i = 0 \\ SSB &,i=1\\ BBSSB&,i=2\\ f(i-2)+f(i-2)+f(i-1)+f(i-1)+f(i-2)&,i>2 \end{cases} \end{array} t=3,f(3)=t=4,f(4)=​SSBSSBBBSSBBBSSBBBSSBSSBSSBBBSSB​∵f(3)=f(1)+f(1)+f(0)+f(0)+f(1)f(4)=f(2)+f(2)+f(1)+f(1)+f(2)∴可推广得:f(i)=⎩⎪⎪⎪⎨⎪⎪⎪⎧​BSSBBBSSBf(i−2)+f(i−2)+f(i−1)+f(i−1)+f(i−2)​,i=0,i=1,i=2,i>2​​
同时容易发现，设发展到第$x$天$B$的个数为$g(x)$，全部字符个数为$\phi (x)$，则有：
g ( x ) = { 1 , x = 0 2 g ( x − 1 ) − 1 , x > 0 , x m o d 2 = 1 2 g ( x − 1 ) + 1 , x > 0 , x m o d 2 = 0 φ ( x ) = { 1 , x = 0 2 φ ( x − 1 ) + 1 , x > 0 , x m o d 2 = 1 2 φ ( x − 1 ) − 1 , x > 0 , x m o d 2 = 0 g(x)= \begin{cases} 1&,x = 0 \\ 2g(x-1)-1&,x>0,x\mod 2 = 1 \\ 2g(x-1)+1&,x>0,x\mod 2 = 0\\ \end{cases}\\ \\ \varphi (x) = \begin{cases} 1 &,x=0 \\ 2\varphi(x-1)+1&,x>0,x\mod 2 = 1 \\ 2\varphi(x-1)-1&,x>0,x\mod 2 = 0\\ \end{cases}\\ g(x)=⎩⎪⎨⎪⎧​12g(x−1)−12g(x−1)+1​,x=0,x>0,xmod2=1,x>0,xmod2=0​φ(x)=⎩⎪⎨⎪⎧​12φ(x−1)+12φ(x−1)−1​,x=0,x>0,xmod2=1,x>0,xmod2=0​
然后就能推算出间谍在哪一个区间，递归求其位置即可

#include
#includeusing namespace std;
int n,k,cnt,tmp;
int len[35],p1,p2,p3,p4;
int num[35],ans;int l(int x)
{if(x%2 == 0) return -1;else return 1;
}void solve(int pre,int sum,int m)//递归
{if(m == 0){ans = pre+1;return ;}if(m == 1){ans = pre+3;return ;}if(m == 2){k -= sum;if(k == 1) ans = pre+1;if(k == 2) ans = pre+2;if(k == 3) ans = pre+5;return ;}int tmp1 = num[m-2];int pre1 = len[m-2];int tmp2 = tmp1+tmp1;int pre2 = pre1+pre1;int tmp3 = tmp2+num[m-3];int pre3 = pre2+len[m-3];int tmp4 = tmp3+num[m-3];int pre4 = pre3+len[m-3];if(k<=sum+tmp1){solve(pre,sum,m-2);return ;}if(k<=sum+tmp2){solve(pre+pre1,sum+tmp1,m-2);return ;}if(k<=sum+tmp3){solve(pre+pre2,sum+tmp2,m-3);return ;}if(k<=sum+tmp4){solve(pre+pre3,sum+tmp3,m-3);return ;}solve(pre+pre4,sum+tmp4,m-2);return ;
}int main()
{len[0] = 1;num[0] = 1;num[1] = 1;for(int i = 1;i <= 30;i ++){len[i] = len[i-1]*2+l(i);//phi(x)num[i+1] = len[i];//g(x)}scanf("%d%d",&n,&k);solve(0,0,n);printf("%d",ans);return 0;
}

T4未改好

#include
#includeusing namespace std;
const long long modnum = 1000000007;
typedef long long ll;
ll n,a[105],f[105][1005][105],p[105],sum,sum2,ans,ti[1005];
int len[105],tmp,num,maxlen;int main()
{ti[0] = 1;for(int i = 1;i <= 1000;i ++){ti[i] = ((ti[i-1]%modnum)*10)%modnum;ti[i] %= modnum;}scanf("%lld",&n);for(int i = 1;i <= n;i ++){scanf("%lld",&a[i]);num = a[i];tmp = 0;while(num){tmp ++;num /= 10;}len[i] = tmp;maxlen += tmp;}p[0] = 1;for(int i = 1;i <= n;i ++){p[i] = ((p[i-1]%modnum)+(((p[i-1]%modnum)*(i%modnum))%modnum))%modnum;p[i] = p[i]%modnum;}for(int i = 1;i <= n;i ++)f[i][0][0] = p[n-1];for(int k = 1;k < n;k ++)for(int i = 1;i <= n;i ++)for(int j = k;j <= maxlen-len[i];j ++)for(int ii = 1;ii <= n;ii ++){if(i!=ii&&len[ii] <= j){sum = ((p[n-k-1]%modnum)*(f[ii][j-len[ii]][k-1]%modnum))%modnum;sum2 = 0;f[i][j][k] += sum%modnum;f[i][j][k] %= modnum;}}for(int i = 1;i <= n;i ++){for(int k = 0;k <= n;k ++){for(int j = k;j <= maxlen;j ++){sum = ((((f[i][j][k]%modnum)*(a[i]%modnum))%modnum)*(ti[j]%modnum))%modnum;ans += (sum%modnum);ans %= modnum;}}}printf("%lld",ans);return 0;
}

10.31

LCS与LIS
最长公共子序列 与 最长上升子序列
P1439 【模板】最长公共子序列
P1233 木棍加工

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！