BUAA_数据结构_5TH_4. 网络打印机选择
BUAA_数据结构_5TH_4. 网络打印机选择
第五次作业链接
1. 树叶节点遍历(树-基础题)
2. 词频统计(树实现)
3. 计算器(表达式计算-表达式树实现)
题目描述:
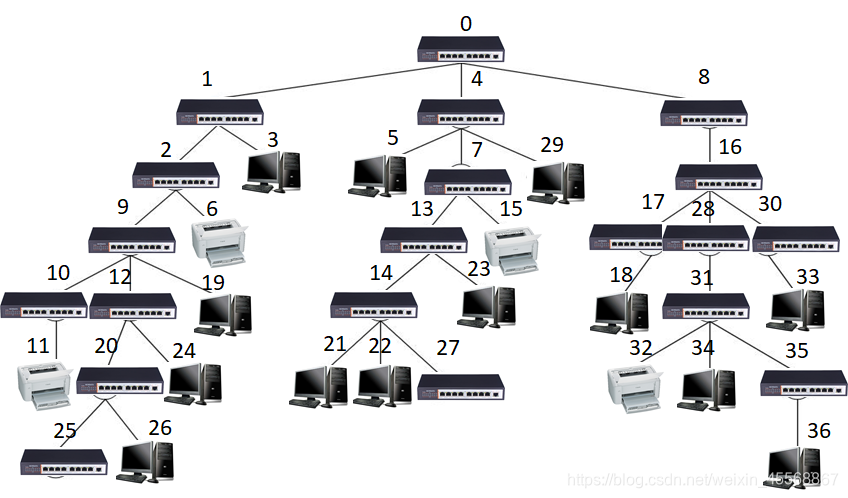
某单位信息网络结构呈树型结构,网络中节点可为交换机、计算机和打印机三种设备,计算机和打印机只能位于树的叶节点上。如要从一台计算机上打印文档,请为它选择最近(即经过交换机最少)的打印机。
在该网络结构中,根交换机编号为0,其它设备编号可为任意有效正整数,每个交换机有8个端口(编号0-7)。当存在多个满足条件的打印机时,选择按树前序遍历序排在前面的打印机。
输入形式
首先从标准输入中输入两个整数,第一个整数表示当前网络中设备数目,第二个整数表示需要打印文档的计算机编号。两整数间以一个空格分隔。假设设备总数目不会超过300。
然后从当前目录下的in.txt读入相应设备配置表,该表每一行构成一个设备的属性,格式如下:
<设备ID> <类型> <设备父节点ID> <端口号>
<设备ID>为一个非负整数,表示设备编号;<类型>分为:0表示交换机、1表示计算机、2表示打印机;<设备父结点ID>为相应结点父结点编号,为一个有效非负整数;<端口号>为相应设备在父结点交换机中所处的端口编号,分别为0-7。由于设备配置表是按设备加入网络时的次序编排的,因此,表中第一行一定为根交换机(其属性为0 0 -1 -1);其它每个设备结点一定在其父设备结点之后输入。每行中设备属性间由一个空格分隔,最后一个属性后有换行符。
输出形式
向控制台输出所选择的打印机编号,及所经过的交换机的编号,顺序是从需要打印文档的计算机开始,编号间以一个空格分隔。
样例输入
37 19
in.txt中的信息如下:
0 0 -1 -1
1 0 0 0
2 0 1 2
3 1 1 5
4 0 0 1
5 1 4 0
6 2 2 2
7 0 4 2
8 0 0 4
9 0 2 0
10 0 9 0
11 2 10 3
12 0 9 2
13 0 7 0
14 0 13 0
15 2 7 3
16 0 8 1
17 0 16 0
18 1 17 5
19 1 9 5
20 0 12 1
21 1 14 1
22 1 14 2
23 1 13 2
24 1 12 5
25 0 20 1
26 1 20 2
27 0 14 7
28 0 16 1
29 1 4 3
30 0 16 7
31 0 28 0
32 2 31 0
33 1 30 2
34 1 31 2
35 0 31 5
36 1 35 3
样例输出
11 9 10
思路
结点存储的内容如下:
#define maxn 8
typedef struct tree_node{int no;//结点编号int type;//结点类型 即 计算机/打印机/交换机int father_no;//父结点编号int deep;//深度struct tree_node *child[maxn];//孩子struct tree_node *father_pos;//父结点指针
}node,*tree_ptr;
建树过程
定义部分
#define max_size 10100
tree_ptr create_node(int no,int type,int father,int deep,tree_ptr pa);//创建一个新的结点
tree_ptr add(int no,int type,int father,int fa_pos);//将读入的结点进行处理并加入树中
tree_ptr find_father(int father);//给出父亲结点的编号,找到父亲结点的指针tree_ptr switches[max_size];//记录所有打印机的指针
int switch_len=0;//打印机指针数组的长度
主函数部分:
int sum,need;scanf("%d%d",&sum,&need);//sum:结点总数 need: 需要打印东西的计算机的编号FILE *in;in=fopen("in.txt","r");int no,type,father,fa_pos;tree_ptr goal=NULL;//用于记录需要打印东西的计算机的指针for(int i=0;i<sum;i++){fscanf(in,"%d %d %d %d",&no,&type,&father,&fa_pos);if(no==need){//如果当前输入的结点是需要打印东西的计算机goal=add(no,type,father,fa_pos);//记录这个计算机的指针}else if(type==2){switches[switch_len++]=add(no,type,father,fa_pos);//如果当前输入结点是打印机,将他的指针加入打印机的指针数组中}else{add(no,type,father,fa_pos);//其他结点 正常添加}}
建树过程中使用到的三个函数
tree_ptr create_node(int no,int type,int father,int deep,tree_ptr pa)//创建一个结点
{tree_ptr temp=(tree_ptr)malloc(sizeof(node));temp->father_no=father;temp->type=type;temp->no=no;temp->deep=deep;temp->father_pos=pa;for(int i=0;i<8;i++){temp->child[i]=NULL;}return temp;
}tree_ptr add(int no,int type,int father,int fa_pos)
{if(root==NULL){//如果此时根节点为空 注:我将根结点作为全局变量 故函数没有传入根节点也可以访问root=create_node(no,type,father,1,NULL);//创建根节点 深度为1,父结点指针为NULLreturn root;}else{tree_ptr pa=find_father(father);//如果此时根结点不为空,我们需要根据父结点编号找到父结点指针tree_ptr now=create_node(no,type,father,pa->deep+1,pa);//新建结点 深度为他父结点的深度+1pa->child[fa_pos]=now;//将父结点和当前结点链接//printf("%d %d\n",pa->no,now->no);return now;}
}tree_ptr find_father(int father)//使用BFS对目前的树进行搜索,如果发现结点编号等于father则说明这个结点就是我们要找的父结点 如果BFS同学们不是很理解可以自己先模拟一下这个过程,如果还是不理解欢迎评论/私戳
{init_queue();//初始化队列enqueue(root);//将根节点加入队列while(!is_empty()){//如果队列不为空tree_ptr temp=dequeue();//出队//printf("%d\n",temp->no);if(temp->no==father) {//判断是不是 是:返回 return temp;}else{//不是:将他非空的子节点加入队列中for(int i=0;i<8;i++){if(temp->child[i]){enqueue(temp->child[i]);}}}}return NULL;//以防万一
}
寻找父结点函数使用到的队列
//好像没啥解释的,标准的循环队列
tree_ptr queue[max_size];
int front,rear,count;
void init_queue();
int is_empty();
void enqueue(tree_ptr temp);
tree_ptr dequeue();
void init_queue()
{for(int i=0;i<max_size;i++){queue[i]=NULL;}front=0;rear=max_size-1;count=0;
}int is_empty()
{return count==0;
}void enqueue(tree_ptr temp)
{rear=(rear+1)%max_size;queue[rear]=temp;count++;
}tree_ptr dequeue()
{tree_ptr temp;temp=queue[front];count--;front=(front+1)%max_size;return temp;
}经历以上步骤 建树结束 使用前序遍历检查一下
void pre_order();
tree_ptr pre_stack[max_size];
int pos_stack;
void push(tree_ptr temp);
tree_ptr pop();
int is_stack_empty();void pre_order()
{pos_stack=-1;memset(pre_stack,'\0',sizeof(pre_stack));push(root);while(!is_stack_empty()){tree_ptr temp=pop();printf("%d %d %d\n",temp->no,temp->type,temp->deep);for(int i=7;i>=0;i--){if(temp->child[i]){push(temp->child[i]);}}}
}void push(tree_ptr temp)
{pre_stack[++pos_stack]=temp;
}tree_ptr pop()
{tree_ptr temp=pre_stack[pos_stack];pos_stack--;return temp;
}int is_stack_empty()
{return pos_stack==-1?1:0;
}
后续思路简要说明
经过上述处理之后,我们得到的东西有 一棵树,需要打印东西的计算机的指针,打印机的指针数组
我们需要求的是从这个计算机到打印机最近的距离,如果距离相同则取前序遍历排在前面的打印机
故我们之后的思路如下:(可能比较麻烦,但是这是我想到的可操作性比较高的方法,如果有同学有不同的思路我们可以交流下~)
对于每一台打印机,找出打印机和要打印东西的这台计算机的最近公共祖先
那么这台打印机与需要打印的计算机之间的距离应为:计算机的深度+打印机深度-2*公共祖先深度
故思路应该比较清晰了:
遍历打印机的指针数组,对于每一个打印机求他和计算机的最近公共祖先,之后由上述公式得出距离,若距离小于之前设定的最小值,则更新最小值,若等于最小值则进行前序遍历判断当前打印机和之前产生最小值的打印机谁在前面。
那么如何求解两个结点的最近公共祖先呢?
思路如下:
从计算机结点出发向上进行遍历(即找他爸爸),直到到达根结点,将这段路径上所有经过的结点进行标记。然后对打印机进行向上遍历,如果在遍历的过程中发现当前结点已经被标记,说明这个结点就是我们要找的公共祖先,跳出即可。
以下为实现
主函数
int min=0x3f3f3f3f;tree_ptr min_switch=NULL;tree_ptr min_LCA_node=NULL;/*printf("%d\n",switch_len);for(int i=0;ino,switches[i]->deep);}*/ visit_computer_to_root(goal);//从计算机结点出发,向上遍历,将经过的结点进行标记for(int i=0;i<switch_len;i++){//遍历打印机的指针数组//printf("main:%d %d\n",switches[i]->no,switches[i]->deep);tree_ptr LCA_node=LCA(switches[i]);//找公共祖先if(LCA_node==NULL) continue;int dist=goal->deep+switches[i]->deep-2*LCA_node->deep;//算距离if(dist<min){//小于则更新min_LCA_node=LCA_node;//记录公共祖先min_switch=switches[i];//记录打印机min=dist;}if(dist==min){//等于则判断是否要更新min_LCA_node=LCA_node;//这里有逻辑错误,应该判断一下在更新的,各位自行改正一下叭min_switch=find_is_ans(min_switch,switches[i]);//判断min=dist;}//printf("min:%d\n",min);}//printf("%d %d %d\n",min_switch->no,min_switch->type,min_switch->deep);
visit_computer_to_root()函数
函数功能:标记计算机到根节点路径上的结点
void visit_computer_to_root(tree_ptr computer_num);
int visit[max_size];void visit_computer_to_root(tree_ptr computer_num)//这段代码中有一些奇怪的地方 下面会解释
{tree_ptr switches_temp[max_size];for(int i=0;i<switch_len;i++){switches_temp[i]=switches[i];}memset(visit,0,sizeof(visit));tree_ptr temp=computer_num;while(temp!=NULL){visit[temp->no]=1;//经过标记为1//printf("%d\n",temp->no);temp=temp->father_pos;//temp更新为他的父结点的指针}for(int i=0;i<switch_len;i++){switches[i]=switches_temp[i];}
}
奇怪的bug
可能有同学会主要到这里并且会感到疑惑,但是这里是因为笔者遇到了一个奇怪的bug,即当我调用 visit_computer_to_root()函数时,会莫名其妙地修改switches(打印机指针数组)的值,笔者检查很久也没有找到原因,只得采用这种看起来有点nt的方法…如果有同学发现了问题请告知我orz
tree_ptr switches_temp[max_size];for(int i=0;i<switch_len;i++){switches_temp[i]=switches[i];}……for(int i=0;i<switch_len;i++){switches[i]=switches_temp[i];}
LCA(tree_ptr switch_num)函数
函数功能:找到打印机和计算机的公共祖先
tree_ptr LCA(tree_ptr switch_num)
{tree_ptr temp1=NULL;temp1=switch_num;//初始化为这个打印机的指针//printf("%d %d %d\n",temp1->no,temp1->father_no,temp1->deep);while(temp1!=NULL){//向上找if(visit[temp1->no]==1){//找到之前访问过的结点//printf("res:%d %d\n",temp1->no,temp1->deep);return temp1;//找到公共祖先,返回}temp1=find_father(temp1->father_no);//printf("father:%d %d\n",temp1->no,temp1->deep);}return NULL;
}
find_is_ans(tree_ptr elder,tree_ptr now)函数
函数功能:当距离等于之前的最小值的时候,判断是否需要更新
tree_ptr find_is_ans(tree_ptr elder,tree_ptr now)//前序遍历
{pos_stack=-1;for(int i=0;i<max_size;i++){pre_stack[i]=NULL;}push(root);while(!is_stack_empty()){tree_ptr temp=pop();if(temp->no==elder->no) return elder;if(temp->no==now->no) return now;for(int i=7;i>=0;i--){//注意加入顺序if(temp->child[i]){push(temp->child[i]);}}}
}
经过上述步骤之后,我们已经得出最小值等其他条件了。参照输出形式进行输出即可
void print_result(tree_ptr goal,tree_ptr min_switch,tree_ptr min_LCA_node)
{printf("%d",min_switch->no);//选取的打印机编号//这部分在找从计算机到公共祖先之间的结点tree_ptr temp=goal;while (temp!=min_LCA_node){printf(" ");temp=temp->father_pos;printf("%d",temp->no);}//这部分在找从打印机到公共祖先之间的结点,由于输出要求路径为从计算机到打印机 故这里使用栈进行存储temp=min_switch;tree_ptr stack[max_size];for(int i=0;i<max_size;i++){stack[i]=NULL;}int pos_res_stack=-1;//以上 栈的初始化while(temp!=min_LCA_node){temp=temp->father_pos;stack[++pos_res_stack]=temp;}pos_res_stack--;//刨除公共祖先while(pos_res_stack!=-1){printf(" %d",stack[pos_res_stack]->no);pos_res_stack--;}
}
完整参考代码
#includeno,switches[i]->deep);}*/ visit_computer_to_root(goal);for(int i=0;i<switch_len;i++){//printf("main:%d %d\n",switches[i]->no,switches[i]->deep);tree_ptr LCA_node=LCA(switches[i]);if(LCA_node==NULL) continue;int dist=goal->deep+switches[i]->deep-2*LCA_node->deep;if(dist<min){min_LCA_node=LCA_node;min_switch=switches[i];min=dist;}if(dist==min){min_LCA_node=LCA_node;min_switch=find_is_ans(min_switch,switches[i]);min=dist;}//printf("min:%d\n",min);}//printf("%d %d %d\n",min_switch->no,min_switch->type,min_switch->deep);print_result(goal,min_switch,min_LCA_node);//pre_order();fclose(in);return 0;
}tree_ptr create_node(int no,int type,int father,int deep,tree_ptr pa)
{tree_ptr temp=(tree_ptr)malloc(sizeof(node));temp->father_no=father;temp->type=type;temp->no=no;temp->deep=deep;temp->father_pos=pa;for(int i=0;i<8;i++){temp->child[i]=NULL;}//printf("%d\n",temp->no);return temp;
}tree_ptr add(int no,int type,int father,int fa_pos)
{if(root==NULL){root=create_node(no,type,father,1,NULL);return root;}else{tree_ptr pa=find_father(father);tree_ptr now=create_node(no,type,father,pa->deep+1,pa);pa->child[fa_pos]=now;//printf("%d %d\n",pa->no,now->no);return now;}
}tree_ptr find_father(int father)
{init_queue();enqueue(root);while(!is_empty()){tree_ptr temp=dequeue();//printf("%d\n",temp->no);if(temp->no==father) {return temp;}else{for(int i=0;i<8;i++){if(temp->child[i]){enqueue(temp->child[i]);}}}}return NULL;
}void init_queue()
{for(int i=0;i<max_size;i++){queue[i]=NULL;}front=0;rear=max_size-1;count=0;
}int is_empty()
{return count==0;
}void enqueue(tree_ptr temp)
{rear=(rear+1)%max_size;queue[rear]=temp;count++;
}tree_ptr dequeue()
{tree_ptr temp;temp=queue[front];count--;front=(front+1)%max_size;return temp;
}void pre_order()
{pos_stack=-1;memset(pre_stack,'\0',sizeof(pre_stack));push(root);while(!is_stack_empty()){tree_ptr temp=pop();printf("%d %d %d\n",temp->no,temp->type,temp->deep);for(int i=7;i>=0;i--){if(temp->child[i]){push(temp->child[i]);}}}
}void push(tree_ptr temp)
{pre_stack[++pos_stack]=temp;
}tree_ptr pop()
{tree_ptr temp=pre_stack[pos_stack];pos_stack--;return temp;
}int is_stack_empty()
{return pos_stack==-1?1:0;
}void visit_computer_to_root(tree_ptr computer_num)
{tree_ptr switches_temp[max_size];for(int i=0;i<switch_len;i++){switches_temp[i]=switches[i];}memset(visit,0,sizeof(visit));tree_ptr temp=computer_num;while(temp!=NULL){visit[temp->no]=1;//printf("%d\n",temp->no);temp=temp->father_pos;}for(int i=0;i<switch_len;i++){switches[i]=switches_temp[i];}
}tree_ptr LCA(tree_ptr switch_num)
{tree_ptr temp1=NULL;temp1=switch_num;//printf("%d %d %d\n",temp1->no,temp1->father_no,temp1->deep);while(temp1!=NULL){if(visit[temp1->no]==1){//printf("res:%d %d\n",temp1->no,temp1->deep);return temp1;}temp1=find_father(temp1->father_no);//printf("father:%d %d\n",temp1->no,temp1->deep);}return NULL;
}tree_ptr find_is_ans(tree_ptr elder,tree_ptr now)
{pos_stack=-1;for(int i=0;i<max_size;i++){pre_stack[i]=NULL;}push(root);while(!is_stack_empty()){tree_ptr temp=pop();if(temp->no==elder->no) return elder;if(temp->no==now->no) return now;for(int i=7;i>=0;i--){if(temp->child[i]){push(temp->child[i]);}}}
}void print_result(tree_ptr goal,tree_ptr min_switch,tree_ptr min_LCA_node)
{printf("%d",min_switch->no);tree_ptr temp=goal;while (temp!=min_LCA_node){printf(" ");temp=temp->father_pos;printf("%d",temp->no);}temp=min_switch;tree_ptr stack[max_size];for(int i=0;i<max_size;i++){stack[i]=NULL;}int pos_res_stack=-1;while(temp!=min_LCA_node){temp=temp->father_pos;stack[++pos_res_stack]=temp;}pos_res_stack--;//刨除公共祖先while(pos_res_stack!=-1){printf(" %d",stack[pos_res_stack]->no);pos_res_stack--;}
}有问题
或bug欢迎私戳/评论
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!