先听我胡说

链表结构和线性结构

很重要！很重要！很重要！

很重要！很重要！

很重要！

无论是学没学过数据结构，都可以想象。来，先入仙下~~~ 世界万物都是离散的，欸？不对，很多美都可以产生于线性。但是其实我们会发现身边的事物是一个递归的世界，一个离散的世界，清醒点，不管世界是怎样，都属于自己。但是，链表就是一个可以复制世界的偷袭者，他可以实现栈、实现队列等等线性的结构，链表是一个非空即是的东西，他除了点和点，就是链。我接下来会描述在我思想里的链表。来吧！good！

目录

（一）不用脑直接看懂链表

（二）轻而易举看到环

（三）一招破解环口

标题一：不用脑看懂链表

因为想到一些朋友可能不理解链表，所以简单讲点

既然是看，那就先看下面这张图

因为这篇文章主题不是介绍链表，所以就不啰嗦了。黑色、红色、蓝色方框分别表示三个不同节点，每个方框（节点）存在上一个节点的下部分，也就是址域。黑色是最外面的那个，也就是head，因为他没有存在包含在其他的方框里面，世界上找不到他，所以head要初始化，而其他的可以通过上一个节点找到就不要初始化。所以链表介绍有头就有链表。

标题二：轻而易举看到环

首先外面先看一下环链长什么样

呃。。。。差不多长这样。一个链表怎么才能知道他有环呢，看图我们可以发现上面的链表的尾

和某个节点相连，而我们最经常想到最暴力的办法就是从头到尾给他遍历一遍，查某个节点的下一个是否已经遍历过，如果查到这样一个节点说明是环链，如果把链表遍历完都没找到说明没有环，显然这样很暴力也有用。但显然这不是你这样聪明人的作法，接下来的一个快慢指针的做法才属于你。

快慢指针经常用于链表，因为链表可以实现多种数据结构，所以快慢指针在整个数据结构中很大用。顾名思义，快慢指针就是一个快指针(fast)和一个慢指针(slow)，指针其实什么意思呢？你可以理解为盒子，一个保存一个节点的盒子。而快慢又是什么意思呢，快慢可以理解为速度上的快慢。

在链表运用中，快指针的速度经常是慢指针的速度的两倍，也就是在同一时间段，快指针从当前节点移动到下一个节点的下一个节点（fast = fast->next->next），而慢指针则从当前指针移动到下一个节点(slow = slow->next)。

一个重要定理：在一个圈中，两个速不一样的车同向行驶一定可以相遇

证明如下：

一个圈的周长为：s

fast、slow的速度为：2v、v

fast和slow相差距离为：m

假设两者在和slow相距n处相遇：

则fast走路程为ks + n - m·····①

slow走路程为qs + n·············②

得：（ks + n - m）/ 2v = （qs + n）/ v

化简整理得：m + n = us ->n = us - m············③

③式代入①式得fast走过路程：(k + u)s - 2m ->  ys - 2m······④

③式代入②式得slow走过路程：(q + s)s - m ->  xy - m·······⑤

由④⑤式可知，当fast走过y - 1圈时，在距离fast 的 s - 2m 处相遇，slow走过（x - 1）圈时，在距离slow的s - m处相遇，【2m可能大于s，但也不影响】，而两者开始距离为m，所以两者会在slow逆方向m处相遇

判环步骤：

一、首先要定义一个fast指针和一个slow指针初始化为指向head这个第一个节点

二、设置一个循环来遍历两指针是否会相遇，两指针按(slow = slow->next, fast = fast->next->next)这个速度走，当fast为空或者下一个节点为空时说明走到表尾，说明没环

例子：leetcode141题

https://leetcode-cn.com/problems/linked-list-cycle/

bool hasCycle(struct ListNode *head) {if (!head) return 0;struct ListNode *fast = head, *slow = head;while (fast && fast->next) {fast = fast->next->next;slow = slow->next;if (fast == slow) {return 1;}}return 0;
}

主题三：一招破解环口

要找链表的还口，最基本的是要判断链表是否有环。好，那先判断是否有环，那你的思路是怎样呢？如果按快慢指针来，判断有环后呢，做什么，好像没有什么思路。这时候暴力可以解决一切，那就来次暴力解决问题？好，那就边遍历边标记遍历过的节点，在遍历过程遇到遍历过的节点那就返回其标记的节点数序。这样显然可以解决问题，但也这不是你想要的，要不然我下面写什么。

接下一起探索环的另一个有趣的定理

有趣的定理：当快慢指针相遇后让慢指针继续走，同时一个新指针new从链头开始走，慢指针和new会在环口相遇

证明：

先引入一张图

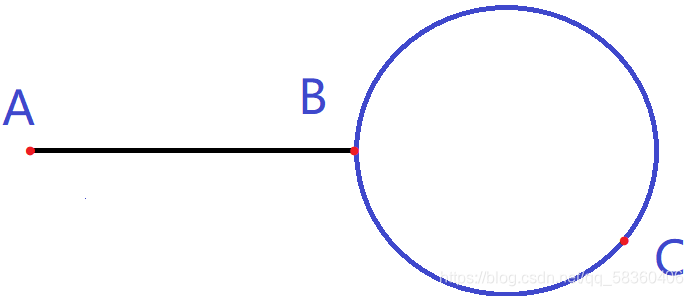
设定一个快指针fast和一个慢指针slow，而且速度是fast=2slow

由图可得：a = AB， b = BC, c = CB

当fast和slow相遇在C点时（为什么会在环内相遇推论在下面），快指针走过了n圈环和a的距离，而慢指针走了a和b的距离，得：

fast = a + n(b + c)

slow = a + b

合并两指针：

2(a + b) = a + n(b + c)

化简得

a = nb + nc - b

再化简得：

a = (n - 1)(b + c) + c

=>a = N(b + c) +c···········①

此时假设一个指针pre指向A点，pre向B点移动，而slow从C点开始在圈内移动，无论slow在环内转多少圈，也就是无论N为多少，两者速度相等，在pre到达B时，slow也会到达B点。

结论：pre从A开始走，slow从C开始走，两者会在B点相遇，而B也正时入环点

找环口步骤：

一、判断是否有环（具体看上面）

二、让一个新指针从head开始遍历，slow从相遇点继续遍历，当着两者相遇则返回相遇时的节点

 例子：leetcode142

https://leetcode-cn.com/problems/linked-list-cycle-ii/

struct ListNode *detectCycle(struct ListNode *head) {if (!head) return 0;struct ListNode *pre = head, *fast = head, *slow = head;while (fast && fast->next) {fast = fast->next->next;slow = slow->next;if (slow == fast) {while (slow != pre) {slow = slow->next;pre = pre->next;}return pre;}}return 0;
}

尾结：经验不足，多多体谅，一起进步，一起debug

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！