18-NIPS-Differential Properties of Sinkhorn Approximation for Learning with Wasserstein Distance

摘要

由于entropic regularization的计算优势，Optimal transport的应用得到了很多关注。但是，在很多情况下，Wasserstein Distance的sinkhorn approximation会被替换成一个regularized版本，不够准确但是容易微分。在这个工作中我们刻画原始的sinkhorn距离的微分特性，证明它和它的regularized版本同样smoothness，并且我们显式地提供了计算它的梯度的高效算法。这个结果对于理论和应用都很有用，一方面，高阶平滑为Wasserstein的近似学习提供了统计保证，另一方面梯度公式使我们可以高效地解决学习和优化问题。

介绍

我们从理论和经验上回顾 到，在优化问题中，原始的sinkhorn距离明显比regularized距离更有利，这确实被注意到有过光滑的倾向。

我们把这作为一个动机来研究sharp sinkhorn的微分特性，其目标是推导一个策略来解决概率分布上的优化和学习问题。

背景

optimal transport理论是探究如何比较一个域上的概率测度。Wasserstein distance是用来表示概率测度的距离的指标。

Wasserstein distance of dicrete measures

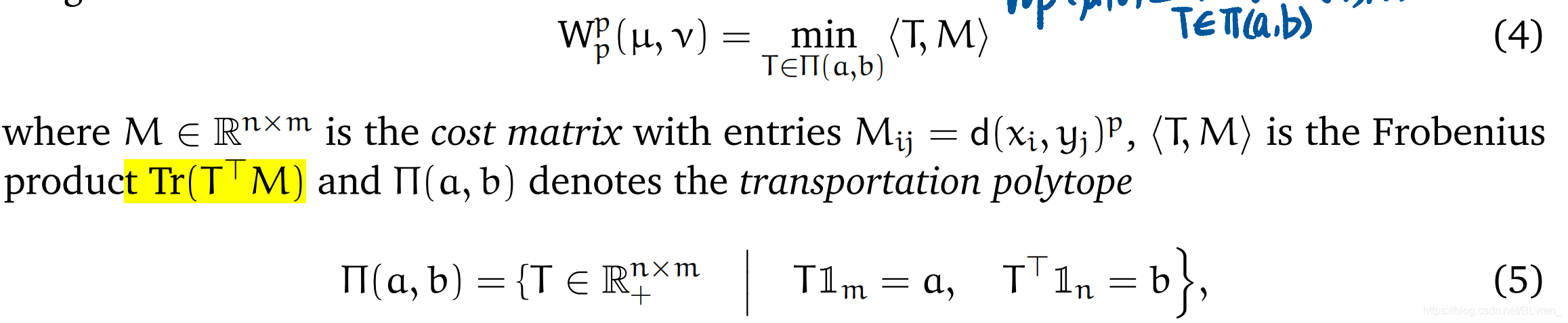
 Regularized Sinkhorn distance Regularized version （加了信息熵项，更容易计算,且对于a,b可微）

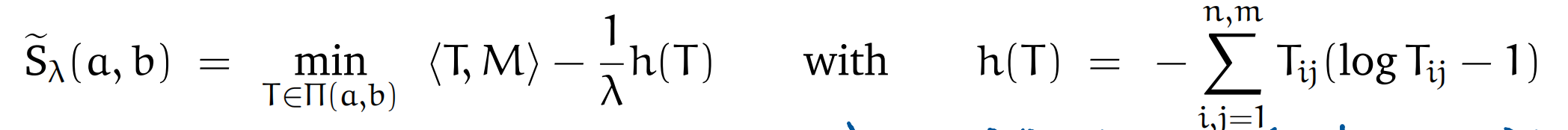
 Sharp Sinkhorn distance, （消除了信息熵对距离的计算）

 使用sharp Sinkhorn distance比使用regularized Sinkorn distance更好，但是目前sharp sinkhorn distance的梯度问题没有解决。

Sharp Sinkhorn distance的微分特性

两个sinkhorn distance都是smooothness, 也就保证了sinkhorn distance的无限微分。（这个结果将使我们能够推导出一个具有Wasserstein loss的监督学习的估计器，并刻画其相应的统计属性，如普遍异质性和学习率）

sinkhorn distance的梯度

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！