目录

一、为什么损失函数不用MSE

二、给逻辑回归代码加上正则化

一、为什么损失函数不用MSE

二、给逻辑回归代码加上正则化

简单的说，就是给代价函数后面加上一个小尾巴惩罚项，比如在线性回归函数中：

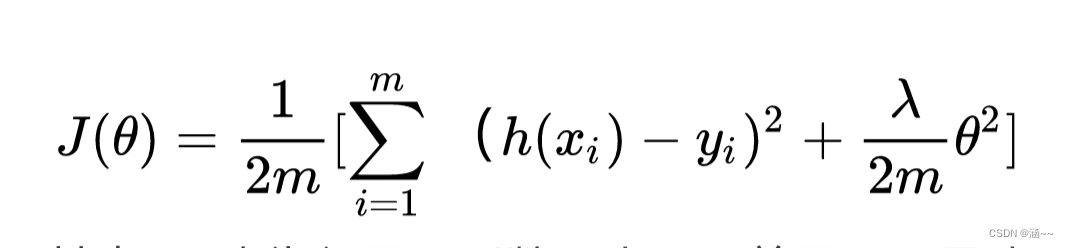
其中，拉姆达称为惩罚项系数。小尾巴前面那一项是我们本来的代价函数，现在加上惩罚项后，我们要使得代价函数最小，则后面的小尾巴也必须要小，小尾巴小的话，那么塞塔就不能太大，如果过小，那么就接近0，也就可以近似看成没有了那个特征。

接下来不断梯度下降，不断迭代以下过程。

代码：

# 实现正则化的代价函数
def costReg(theta, X, y, learningRate):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)first = np.multiply(-y, np.log(sigmoid(X * theta.T)))second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))return np.sum(first - second) / len(X) + reg# 实现正则化的梯度函数
def gradientReg(theta, X, y, learningRate):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)parameters = int(theta.ravel().shape[1])grad = np.zeros(parameters)error = sigmoid(X * theta.T) - yfor i in range(parameters):term = np.multiply(error, X[:,i])if (i == 0):grad[i] = np.sum(term) / len(X)else:grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])return grad#sigmoid函数
def sigmoid(z):return 1 / (1 + np.exp(-z))#预测函数
def predict(theta, X):probability = sigmoid(X * theta.T)return [1 if x >= 0.5 else 0 for x in probability]

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！