人工智能数学基础之线性代数(三)
前言
本文只会记录人工智能中所用到的线性代数知识,并不会记录大学线性代数教材中的所有知识。
现在CSDN不能发超长的文章了,只能分成多篇发布。
人工智能数学基础之线性代数(一)
人工智能数学基础之线性代数(二)
人工智能数学基础之线性代数(三)
矩阵的逆
方阵的行列式
定义6 由 n n n阶方阵 A A A的元素所构成的行列式,称为方阵 A A A的行列式,记作 ∣ A ∣ |A| ∣A∣或 d e t A det A detA。
由 A A A确定 ∣ A ∣ |A| ∣A∣的这个运算满足下述运算规律(设 A , B A,B A,B为 n n n阶方阵, λ \lambda λ为数):
- ∣ A T ∣ = ∣ A ∣ |A^T|=|A| ∣AT∣=∣A∣ (行列式性质1)
- ∣ λ A ∣ = λ n ∣ A ∣ |\lambda A| = \lambda^n |A| ∣λA∣=λn∣A∣
- ∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB| = |A||B| ∣AB∣=∣A∣∣B∣
行列式 ∣ A ∣ |A| ∣A∣的各个元素的代数余子式 A i j A_{ij} Aij所构成的如下的矩阵(注意是转置排法)
A ∗ = ( A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋮ A 1 n A 2 n ⋯ A n n ) , A^* =\begin{pmatrix} A_{11} &A_{21} & \cdots & A_{n1}\\ A_{12} &A_{22} & \cdots & A_{n2}\\ \vdots &\vdots && \vdots \\ A_{1n} &A_{2n} & \cdots & A_{nn}\\ \end{pmatrix} , A∗= A11A12⋮A1nA21A22⋮A2n⋯⋯⋯An1An2⋮Ann ,
称为矩阵 A A A的伴随矩阵,简称伴随阵。
试证
A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^*A = |A|E AA∗=A∗A=∣A∣E
证
A A ∗ = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ) ( A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋮ A 1 n A 2 n ⋯ A n n ) = ( ∣ A ∣ ∣ A ∣ ⋱ ∣ A ∣ ) = ∣ A ∣ E AA^* =\begin{pmatrix} a_{11} &a_{12} & \cdots & a_{1n}\\ a_{21} &a_{22} & \cdots & a_{2n}\\ \vdots &\vdots && \vdots \\ a_{n1} &a_{n2} & \cdots & a_{nn}\\ \end{pmatrix} \begin{pmatrix} A_{11} &A_{21} & \cdots & A_{n1}\\ A_{12} &A_{22} & \cdots & A_{n2}\\ \vdots &\vdots && \vdots \\ A_{1n} &A_{2n} & \cdots & A_{nn}\\ \end{pmatrix} = \begin{pmatrix} |A| & & & \\ &|A| & & \\ & &\ddots& \\ & & & |A|\\ \end{pmatrix} = |A| E AA∗= a11a21⋮an1a12a22⋮an2⋯⋯⋯a1na2n⋮ann A11A12⋮A1nA21A22⋮A2n⋯⋯⋯An1An2⋮Ann = ∣A∣∣A∣⋱∣A∣ =∣A∣E
逆矩阵
设 A A A为 n n n阶方阵( n × n n×n n×n),若存在 n n n阶方阵 B B B使得: A B = B A = E AB=BA=E AB=BA=E,则称 A A A是可逆的(或非奇异的)且矩阵 B B B是矩阵 A A A的逆矩阵,记为 A − 1 = B A^{-1} = B A−1=B。
矩阵 B B B称为 A A A的逆矩阵,简称逆阵。
若 B B B和 C C C均为 A A A的逆矩阵,则
B = B E = B ( A C ) = ( B A ) C = E C = C B = BE= B(AC) = (BA)C = EC = C B=BE=B(AC)=(BA)C=EC=C
因此一个矩阵最多有一个逆矩阵。
定理1 若矩阵 A A A可逆,则 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0
证 A A A可逆,即有 A − 1 A^{-1} A−1,使 A A − 1 = E AA^{-1}=E AA−1=E。故 ∣ A ∣ ⋅ ∣ A − 1 ∣ = ∣ E ∣ = 1 |A|\cdot |A^{-1}| = |E| =1 ∣A∣⋅∣A−1∣=∣E∣=1,所以 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0。
定理2 若 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0,则矩阵 A A A可逆,且
A − 1 = 1 ∣ A ∣ A ∗ (1) A^{-1} = \frac{1}{|A|}A^* \tag{1} A−1=∣A∣1A∗(1)
其中 A ∗ A^* A∗为矩阵 A A A的伴随阵。
证
我们已知
A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^*A = |A|E AA∗=A∗A=∣A∣E
因为 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0,(等式两边同时乘以 1 ∣ A ∣ \frac{1}{|A|} ∣A∣1)故有
A 1 ∣ A ∣ A ∗ = 1 ∣ A ∣ A ∗ A = E , A\frac{1}{|A|} A^* = \frac{1}{|A|}A^*A =E, A∣A∣1A∗=∣A∣1A∗A=E,
所以,按逆矩阵的定义,即知 A A A可逆,且
A − 1 = 1 ∣ A ∣ A ∗ . A^{-1}= \frac{1}{|A|}A^*. A−1=∣A∣1A∗.
当 ∣ A ∣ = 0 |A|=0 ∣A∣=0时, A A A称为奇异矩阵,否则称非奇异矩阵。由上面两定理可知: A A A是可逆矩阵的充分必要条件是 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0,即可逆矩阵就是非奇异矩阵。
由定理2,可得下述推论。
推论 若 A B = E AB=E AB=E(或 B A = E BA=E BA=E),则 B = A − 1 B=A^{-1} B=A−1。
证 ∣ A ∣ ⋅ ∣ B ∣ = ∣ E ∣ = 1 |A|\cdot |B| =|E| = 1 ∣A∣⋅∣B∣=∣E∣=1,故 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0,因而 A − 1 A^{-1} A−1存在,于是
B = E B = ( A − 1 A ) B = A − 1 ( A B ) = A − 1 E = A − 1 。 B = EB = (A^{-1}A)B = A^{-1}(AB) = A^{-1}E = A^{-1}。 B=EB=(A−1A)B=A−1(AB)=A−1E=A−1。
方阵的逆阵满足下述运算规律:
-
若 A A A可逆,则 A − 1 A^{-1} A−1亦可逆,且 ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A
-
若 A A A可逆,数 λ ≠ 0 \lambda \neq 0 λ=0,则 λ A \lambda A λA可逆,且 ( λ A ) − 1 = 1 λ A − 1 (\lambda A)^{-1}= \frac{1}{\lambda}A^{-1} (λA)−1=λ1A−1
-
若 A , B A,B A,B为同阶矩阵且均可逆,则 A B AB AB亦可逆,且
( A B ) − 1 = B − 1 A − 1 (AB)^{-1} = B^{-1}A^{-1} (AB)−1=B−1A−1
证 ( A B ) ( B − 1 A − 1 ) = A ( B B − 1 ) A − 1 = A A − 1 = E (AB)(B^{-1}A^{-1}) = A(BB^{-1})A^{-1}=AA^{-1} =E (AB)(B−1A−1)=A(BB−1)A−1=AA−1=E ,即有 ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1。 -
若 A A A可逆,则 A T A^T AT亦可逆,且 ( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}= (A^{-1})^T (AT)−1=(A−1)T
证 A T ( A − 1 ) T = ( A − 1 A ) T = E T = E A^T(A^{-1})^T=(A^{-1}A)^T=E^T=E AT(A−1)T=(A−1A)T=ET=E
矩阵的秩
矩阵的初等变换
为了引进矩阵的初等变换,先来分析用消元法解线性方程组的例子。
引例 求解线性方程组

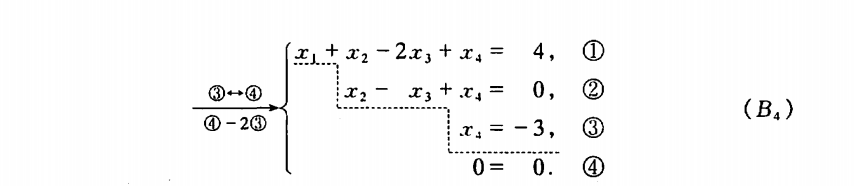
在上述消元过程中,始终把方程组看作一个整体。其中用到三种变换,即:交换方程次序(如 ( B 1 ) 中① ↔ ② (B_1)\text{中}①\leftrightarrow ② (B1)中①↔②);以不等于0的数乘某个方程(如 ( B 3 ) 中② × 1 2 (B_3)中②\times \frac{1}{2} (B3)中②×21);一个方程加上另一个方程的 k k k倍(如 ( B 2 ) 中③ − 2 ① (B_2)中③-2① (B2)中③−2①)。
由于这三种变换都是可逆的,因此变换前的方程组与变换后的方程组是同解的。
在上述变换过程中,实际上只对方程组的系数和常数进行运算,未知数并未参与运算。因此,若记方程组 ( 1 ) (1) (1)的增广矩阵为
B = ( A , b ) = ( 2 − 1 − 1 1 2 1 1 − 2 1 4 4 − 6 2 − 2 4 3 6 − 9 7 9 ) , B =(A,b) =\begin{pmatrix} 2 &-1 & -1 & 1 &2\\ 1 &1 & -2 & 1 &4\\ 4 &-6 &2& -2 &4 \\ 3 &6 & -9 & 7 & 9\\ \end{pmatrix}, B=(A,b)= 2143−11−66−1−22−911−272449 ,
那么上述对方程组的变换完全可以转换为对矩阵 B B B的变换。把方程组的上述三种同解变换移植到矩阵上,就得到句子的三种初等变换。
定义1 下面三种变换称为矩阵的初等行变换:
- 对调两行(对调 i , j i,j i,j两行,记作 r i ↔ r j r_i \leftrightarrow r_j ri↔rj)
- 以数 k ≠ 0 k \neq0 k=0乘某一行中的所有元素(第 i i i行乘 k k k,记作 r i × k r_i \times k ri×k)
- 把某一行所有元素的 k k k倍加到另一行对应的元素上去(第 j j j行的 k k k倍加到第 i i i行上,记作 r i + k r j r_i+kr_j ri+krj)
把定义中的“行”换成“列”,即得矩阵的初等列变换的定义。
矩阵的初等行变换与初等列变换,统称为初等变换。
显然,三种初等变换都是可逆的(操作),且其逆变换是同一类型的初等变换;
- 变换 r i ↔ r j r_i \leftrightarrow r_j ri↔rj的逆变换就是其本身;
- 变换 r i × k r_i \times k ri×k的逆变换为 r i × ( 1 k ) r_i \times \left(\frac{1}{k}\right) ri×(k1)(或记作 r i ÷ k r_i \div k ri÷k)
- 变换 r i + k r j r_i + kr_j ri+krj的逆变换为 r i + ( − k ) r j r_i + (-k)r_j ri+(−k)rj(或记作 r i − k r j r_i - kr_j ri−krj)
如果矩阵 A A A经过有限次初等行变换变成矩阵 B B B,就称矩阵 A A A与 B B B行等价,记作 A ∼ r B A\overset{r}{\sim}B A∼rB;
如果矩阵 A A A经过有限次初等列变换变成矩阵 B B B,就称矩阵 A A A与 B B B列等价,记作 A ∼ c B A\overset{c}{\sim}B A∼cB;
如果矩阵 A A A经过有限次初等变换变成矩阵 B B B,就称为矩阵 A A A与 B B B等价,记作 A ∼ B A \sim B A∼B。
矩阵之间的等价关系具有下列性质:
- 反身性 A ∼ A A \sim A A∼A
- 对称性 若 A ∼ B A \sim B A∼B,则 B ∼ A B \sim A B∼A
- 传递性 若 A ∼ B , B ∼ C A \sim B, B \sim C A∼B,B∼C,则 A ∼ C A \sim C A∼C
下面用矩阵的初等行变换来解方程组 ( 1 ) (1) (1),其过程可与方程组 ( 1 ) (1) (1)的消元过程一一对照。
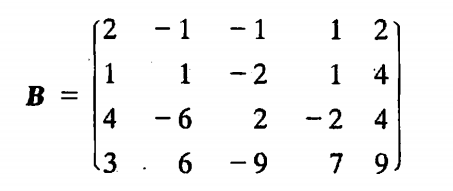


矩阵 B 4 B_4 B4和 B 5 B_5 B5都称为行阶梯形矩阵,其特点是:
可画出一条阶梯线,线的下方全为0;
每个台阶只有一行,台阶数即使非零行的行数;
阶梯线的竖线后面的一个元素为非零元,也就是非零行的第一个非零元;
行阶梯形矩阵 B 5 B_5 B5还称为行最简形矩阵,其特点是:非零行的第一个非零元为 1 1 1,且这些非零元所在的列的其他元素都为 0 0 0。
对于任何矩阵 A m × n A_{m \times n} Am×n,总可经过有限次初等行变换把它变为行阶梯形矩阵和行最简形矩阵。
对行最简形矩阵再施以初等列变换,可变成一种形状更简单的矩阵,称为标准形,例如:
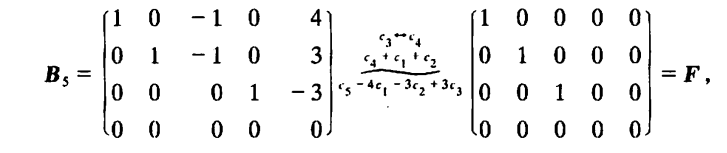
矩阵 F F F称为矩阵 B B B的标准形,其特点是: F F F的左上角是一个单位矩阵,其余元素全为 0 0 0。
对于 m × n m \times n m×n矩阵 A A A,总可经过初等变换(行变换或列变换)把它化为标准形
F = ( E r O O O ) m × n F = \begin{pmatrix} E_r & O \\ O & O \\ \end{pmatrix} _{m \times n} F=(ErOOO)m×n
此标准形由 m , n , r m,n,r m,n,r三个数完全确定,其中 r r r就是行阶梯形矩阵中非零行的行数。
定理1 设 A A A与 B B B为 m × n m \times n m×n矩阵,那么:
- A ∼ r B A \overset{r}{\sim} B A∼rB的充要条件是存在 m m m阶可逆矩阵 P P P;使 P A = B PA=B PA=B;
- A ∼ c B A \overset{c}{\sim} B A∼cB的充要条件是存在 n n n阶可逆矩阵 Q Q Q;使 A Q = B AQ=B AQ=B;
- A ∼ B A \sim B A∼B的充要条件是存在 m m m阶可逆矩阵 P P P及 n n n阶可逆矩阵 Q Q Q,使 P A Q = B PAQ=B PAQ=B。
为了证明这个定理,我们引进初等矩阵的知识。
定义2 由单位阵 E E E经过一次初等变换得到的矩阵称为初等矩阵。
三种初等变换对应有三种初等矩阵。
(1) 把单位阵中第 i , j i,j i,j两行对调(或两列对调),得初等矩阵
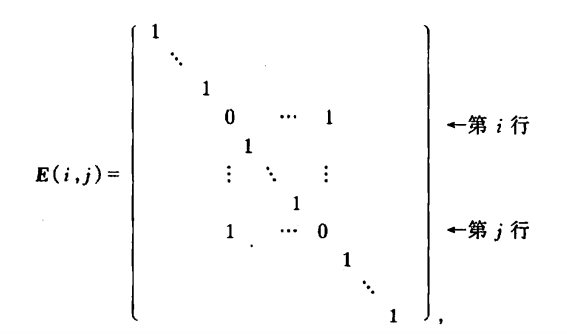
用 m m m阶初等矩阵 E m ( i , j ) E_m(i,j) Em(i,j)左乘矩阵 A = ( a i j ) m × n A=(a_{ij})_{m \times n} A=(aij)m×n,得
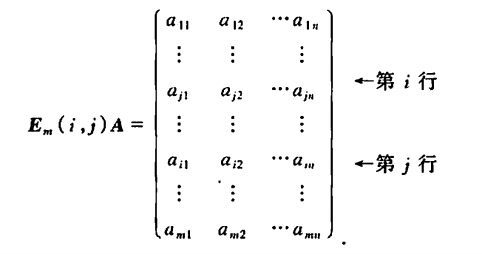
其结果相当于对矩阵 A A A施行第一种初等行变换。
∣ E ( i , j ) ∣ = − 1 ≠ 0 |E(i,j)| = -1 \neq 0 ∣E(i,j)∣=−1=0,所以是可逆的。因为 ∣ E ∣ = 1 |E|=1 ∣E∣=1,对 E E E交换两行或两列,行列式变号。
(2)以数 k ≠ 0 k \neq 0 k=0乘单位阵的第 i i i行(或第 i i i列),得初等矩阵
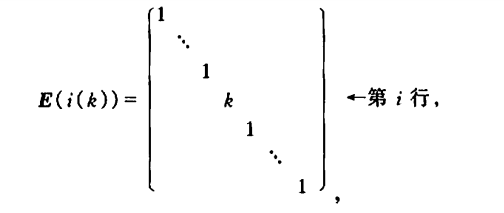
可以验知:以 E m ( i ( k ) ) E_m(i(k)) Em(i(k))左乘矩阵 A A A,其结果相当于以数 k k k乘 A A A的第 i i i行 ( r i × k ) (r_i \times k) (ri×k);
行列式某行乘以某个数 k k k,等于用 k k k乘以此行列式,所以行列式不为零,可逆。
或因此矩阵是对角矩阵,行列式为 1 × 1 ⋯ × k ⋯ × 1 = k 1 \times 1 \cdots \times k \cdots \times 1 = k 1×1⋯×k⋯×1=k。
(3) 以 k k k乘 E E E的第 j j j行加到第 i i i行上或以 k k k乘 E E E的第 i i i列加到第 j j j列上,得初等矩阵
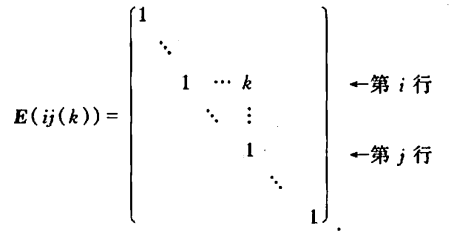
可以验知:以 E m ( i j ( k ) ) E_m(ij(k)) Em(ij(k))左乘矩阵 A A A,其结果相当于把 A A A的第 j j j行乘 k k k加到第 i i i行 ( r i + k r j ) (r_i+kr_j) (ri+krj)。
得到的矩阵的行列式还是为 1 ≠ 0 1 \neq 0 1=0,所以可逆。
归纳上面的讨论,可得
性质1 设 A A A是一个 m × n m \times n m×n矩阵,对 A A A施行一次初等行变换,相当于在 A A A的左边乘以相应的 m m m阶初等矩阵;对 A A A施行一次初等列变换,相当于在 A A A的右边乘以相应的 n n n阶初等矩阵。
性质2 方阵 A A A可逆的充要条件是存在有限个初等矩阵 P 1 , P 2 , ⋯ , P l P_1,P_2,\cdots,P_l P1,P2,⋯,Pl,使 A = P 1 P 2 ⋯ P l A = P_1P_2\cdots P_l A=P1P2⋯Pl。
证 先证充分性。设 A = P 1 P 2 ⋯ P l A = P_1P_2\cdots P_l A=P1P2⋯Pl,因初等矩阵可逆,有限个可逆矩阵的乘积仍可逆,故 A A A可逆。
再证必要性 设 n n n阶方阵 A A A可逆,且 A A A的标准形矩阵为 F F F,由于 F ∼ A F \sim A F∼A,知 F F F经过有限次初等变换可化为 A A A,即有初等矩阵 P 1 , P 2 , ⋯ , P l P_1,P_2,\cdots,P_l P1,P2,⋯,Pl,使
A = P 1 ⋯ P s F P s + 1 ⋯ P l , A = P_1 \cdots P_s FP_{s+1}\cdots P_l, A=P1⋯PsFPs+1⋯Pl,
因为 A A A可逆,所以 ∣ A ∣ = ∣ P 1 ∣ ⋅ ∣ P 2 ∣ ⋅ ⋯ ∣ P l ∣ ≠ 0 |A| = |P_1|\cdot |P_2| \cdot \cdots |P_l| \neq 0 ∣A∣=∣P1∣⋅∣P2∣⋅⋯∣Pl∣=0,所以 ∣ P 1 ∣ , ∣ P 2 ∣ , ⋯ , ∣ P l ∣ |P_1| ,|P_2|,\cdots,|P_l| ∣P1∣,∣P2∣,⋯,∣Pl∣都不等于零。
所以 P 1 , ⋯ , P l P_1,\cdots,P_l P1,⋯,Pl也都可逆,故标准形矩阵 F F F可逆。假设
F = ( E r O O O ) n × n F = \begin{pmatrix} E_r & O \\ O & O \\ \end{pmatrix} _{n \times n} F=(ErOOO)n×n
中的$ r < n ,则 ,则 ,则|F| =0 ,与 ,与 ,与F 可逆矛盾,因此必有 可逆矛盾,因此必有 可逆矛盾,因此必有r=n ,即 ,即 ,即F=E$,从而
A = P 1 P 2 ⋯ P l . A=P_1P_2\cdots P_l. A=P1P2⋯Pl.
下面应用初等矩阵的知识来证明定理1。
定理1的证明
- 依据 A ∼ r B A\overset{r}{\sim}B A∼rB的定义和初等矩阵的性质,有
A ∼ r B ⇔ A 经过有限次初等行变换变成 B ⇔ 存在有限个 m 阶初等矩阵 P 1 , P 2 , ⋯ , P l ,使 P l ⋯ P 2 P 1 A = B ⇔ 存在 m 阶可逆矩阵 P ,使 P A = B . \begin{aligned} A\overset{r}{\sim}B &\Leftrightarrow A经过有限次初等行变换变成B \\ &\Leftrightarrow 存在有限个m阶初等矩阵P_1,P_2,\cdots,P_l,使P_l\cdots P_2P_1A=B\\ &\Leftrightarrow 存在m阶可逆矩阵P,使PA=B. \end{aligned} A∼rB⇔A经过有限次初等行变换变成B⇔存在有限个m阶初等矩阵P1,P2,⋯,Pl,使Pl⋯P2P1A=B⇔存在m阶可逆矩阵P,使PA=B.
类似可证明2. 3.
推论 方阵 A A A可逆的充分必要条件是 A ∼ r E A\overset{r}{\sim}E A∼rE。
证 A A A可逆 ⇔ \Leftrightarrow ⇔ 存可逆阵 P P P(即 A A A的逆阵),使 P A = E PA=E PA=E,所以 A ∼ r E A\overset{r}{\sim}E A∼rE。
定理1表明,如果 A ∼ r B A\overset{r}{\sim}B A∼rB,即 A A A经过一系列初等变换可以变为 B B B,则有可逆矩阵 P P P,使 P A = B PA=B PA=B。那么,如何求出这个可逆矩阵 P P P?
由于
P A = B ⇔ { P A = B , P E = P ⇔ P ( A , E ) = ( B , P ) ⇔ ( A , E ) ∼ r ( B , P ) PA=B \Leftrightarrow \begin{cases} PA = B, \\ PE=P \end{cases} \Leftrightarrow P(A,E) = (B,P) \Leftrightarrow (A,E) \overset{r}{\sim} (B,P) PA=B⇔{PA=B,PE=P⇔P(A,E)=(B,P)⇔(A,E)∼r(B,P)
因此,如果对矩阵 ( A , E ) (A,E) (A,E)作初等行变换,那么,当把 A A A变为 B B B时, E E E就变为 P P P。
于是就得到了求逆矩阵的一种新方法。
矩阵的秩
定义 在 m × n m \times n m×n的矩阵 A A A中,任取 k k k行与 k k k列,位于这些行列交叉处的 k 2 k^2 k2个元素,不改变它们在 A A A中所处的位置次序而得的 k k k阶行列式,称为矩阵 A A A的 k k k阶子式。
m × n m \times n m×n矩阵 A A A的 k k k阶子式共有 C m k ⋅ C n k C_m^k \cdot C_n^k Cmk⋅Cnk个。
定义 设在矩阵 A A A中有一个不等于0的 r r r阶子式 D D D,且所有 r + 1 r+1 r+1阶子式(如果存在的话)全等于0,那么 D D D称为矩阵 A A A的最高阶非零子式,数 r r r称为矩阵 A A A的秩,记作 R ( A ) R(A) R(A)。并规定零矩阵的秩等于0。
比如,我们上面知道,一个 m × n m \times n m×n矩阵 A A A,它的标准形
( E r O O O ) m × n \begin{pmatrix} E_r & O \\ O & O \\ \end{pmatrix} _{m \times n} (ErOOO)m×n
由数 r r r完全确定,这个数就是 A A A的行阶梯形中非零行的行数,也就是矩阵 A A A的秩。
显然,若 A A A为 m × n m \times n m×n矩阵,则 0 ≤ R ( A ) ≤ min { m , n } 0 \leq R(A) \leq \min\{m,n\} 0≤R(A)≤min{m,n}
由于行列式与其转置行列式相等,因此 A T A^T AT的子式与 A A A的子式对应相等,从而 R ( A T ) = R ( A ) R(A^T) = R(A) R(AT)=R(A)。
对于 n n n阶矩阵 A A A,由于 A A A的 n n n阶子式只有一个 ∣ A ∣ |A| ∣A∣,故当 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0时 R ( A ) = n R(A)=n R(A)=n;
当 ∣ A ∣ = 0 |A| =0 ∣A∣=0时 R ( A ) < n R(A) < n R(A)<n。
可见可逆矩阵的秩等于矩阵的阶数,不可逆矩阵的秩小于矩阵的阶数。因此,可逆矩阵又称为满秩矩阵,不可逆矩阵(奇异矩阵)又称为降秩矩阵。
定理2 若 A ∼ B A \sim B A∼B,则 R ( A ) = R ( B ) R(A) = R(B) R(A)=R(B)。
推论 若可逆矩阵 P , Q P,Q P,Q使 P A Q = B PAQ = B PAQ=B,则 R ( A ) = R ( B ) R(A) = R(B) R(A)=R(B)。
秩的性质
- 0 ≤ R ( A m × n ) ≤ min ∣ m , n ∣ 0 \leq R(A_{m \times n}) \leq \min |m,n| 0≤R(Am×n)≤min∣m,n∣
- R ( A T ) = R ( A ) R(A^T) = R(A) R(AT)=R(A)
- 若 A ∼ B A \sim B A∼B,则 R ( A ) = R ( B ) R(A) = R(B) R(A)=R(B)
- 若 P P P、 Q Q Q可逆,则 R ( P A Q ) = R ( A ) R(PAQ) = R(A) R(PAQ)=R(A)
- max { R ( A ) , R ( B ) } ≤ R ( A , B ) ≤ R ( A ) + R ( B ) \max \{R(A),R(B)\} \leq R(A,B) \leq R(A) + R(B) max{R(A),R(B)}≤R(A,B)≤R(A)+R(B)
- 特别第,当 B = b B=b B=b为非零列向量时,有
R ( A ) ≤ R ( A , b ) ≤ R ( A ) + 1 R(A) \leq R(A,b) \leq R(A) +1 R(A)≤R(A,b)≤R(A)+1
- 特别第,当 B = b B=b B=b为非零列向量时,有
- R ( A + B ) ≤ R ( A ) + R ( B ) R(A+B) \leq R(A) + R(B) R(A+B)≤R(A)+R(B)
- R ( A B ) ≤ min { R ( A ) , R ( B ) } R(AB) \leq \min \{R(A),R(B) \} R(AB)≤min{R(A),R(B)}
- 若 A m × n B n × l = O A_{m \times n}B_{n \times l} = O Am×nBn×l=O,则 R ( A ) + R ( B ) ≤ n R(A) + R(B) \leq n R(A)+R(B)≤n
线性方程组的解
设有 n n n个未知数 m m m个方程的线性方程组
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 , a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 , ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m , (3) \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n= b_1, \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n= b_2, \\ \cdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n= b_m, \\ \end{cases} \tag{3} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1,a21x1+a22x2+⋯+a2nxn=b2,⋯am1x1+am2x2+⋯+amnxn=bm,(3)
( 3 ) (3) (3)式可以写成以向量 x x x为未知元的向量方程
A x = b , Ax = b, Ax=b,
定理3 n n n元线性方程组 A x = b Ax=b Ax=b
- 无解的充分必要条件是 R ( A ) < R ( A , b ) R(A) < R(A,b) R(A)<R(A,b) (即出现了 0 = b 0 = b 0=b的情况,其中 b ≠ 0 b \neq 0 b=0)
- 有唯一解的充分必要条件是 R ( A ) = R ( A , b ) = n R(A) = R(A,b) = n R(A)=R(A,b)=n
- 有无限多解的充分必要条件是 R ( A ) = R ( A , b ) < n R(A) = R(A,b) < n R(A)=R(A,b)<n
这里的 n n n是未知数的个数。
定理4 n n n元齐次线性方程组 A x = 0 Ax =0 Ax=0有非零解的充分必要条件是 R ( A ) < n R(A) < n R(A)<n
定理5 线性方程组 A x = b Ax =b Ax=b有解的充分必要条件是 R ( A ) = R ( A , b ) R(A) = R(A,b) R(A)=R(A,b)
用克拉默法则来看的话,
如果 A A A是方阵, A x = 0 Ax=0 Ax=0有非零解的条件是, ∣ A ∣ = 0 |A| =0 ∣A∣=0,即 R ( A ) < n R(A) < n R(A)<n。
我们知道
逆矩阵存在 ⇔ ∣ A ∣ ≠ 0 ⇔ R ( A ) = n \Leftrightarrow |A| \neq 0 \Leftrightarrow R(A) =n ⇔∣A∣=0⇔R(A)=n
正交性
标量积
两个 R n R^n Rn中的向量 x x x和 y y y可以看成是 n × 1 n \times 1 n×1矩阵。构造矩阵乘积 x T y x^Ty xTy。这个乘积为一个 1 × 1 1\times 1 1×1矩阵,可看成是一个 R 1 R^1 R1中的向量,或一个实数(标量)。
乘积 x T y x^Ty xTy称为 x x x和 y y y的标量积(scalar product)或内积。
x T y = ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ c o s θ = ∑ i = 1 n x i y i = ⟨ x , y ⟩ x^Ty = ||x||\,\, ||y|| \, cos \theta = \sum_{i=1}^n x_i y_i = \langle x,y \rangle xTy=∣∣x∣∣∣∣y∣∣cosθ=i=1∑nxiyi=⟨x,y⟩
如果 x T y = 0 x^Ty=0 xTy=0,则称向量 x x x和 y y y为正交的。
内积空间
一个向量空间 V V V上的内积为 V V V上的运算,它将 V V V中的向量 x x x和 y y y与一个实数 ⟨ x , y ⟩ \langle x,y \rangle ⟨x,y⟩关联,并满足下列条件:
- ⟨ x , y ⟩ ≥ 0 \langle x,y \rangle \geq 0 ⟨x,y⟩≥0,等号成立的充要条件是 x = 0 x=0 x=0
- 对 V V V中所有的 x x x和 y y y,有 ⟨ x , y ⟩ = ⟨ y , x ⟩ \langle x,y \rangle = \langle y,x \rangle ⟨x,y⟩=⟨y,x⟩
- 对 V V V中所有的 x , y , z x,y,z x,y,z及所有的标量 α , β \alpha,\beta α,β,有 ⟨ α x + β y , z ⟩ = α ⟨ x , z ⟩ + β ⟨ y , z ⟩ \langle \alpha x + \beta y,z \rangle = \alpha \langle x,z \rangle + \beta \langle y,z \rangle ⟨αx+βy,z⟩=α⟨x,z⟩+β⟨y,z⟩
一个定义了内积的向量空间 V V V称为内积空间。
正交集
定义 令 v 1 , v 2 , ⋯ , v n v_1,v_2,\cdots,v_n v1,v2,⋯,vn为一内积空间 V V V中的非零向量。若 i ≠ j i \neq j i=j时有 ⟨ v i , v j ⟩ = 0 \langle v_i, v_j \rangle = 0 ⟨vi,vj⟩=0,则 { v 1 , v 2 , ⋯ , v n } \{v_1,v_2,\cdots,v_n\} {v1,v2,⋯,vn}称为向量的正交集。
定理 若 ⟨ v i , v j ⟩ = 0 \langle v_i, v_j \rangle = 0 ⟨vi,vj⟩=0,则 { v 1 , v 2 , ⋯ , v n } \{v_1,v_2,\cdots,v_n\} {v1,v2,⋯,vn}为一内积空间 V V V中非零向量的正交集,则 v 1 , v 2 , ⋯ , v n v_1,v_2,\cdots,v_n v1,v2,⋯,vn是线性无关的。
规范正交
定义 规范正交的向量集合是单位向量的正交集。
集合 { u 1 , u 2 , ⋯ , u n } \{u_1,u_2,\cdots, u_n\} {u1,u2,⋯,un}是规范正交集的充要条件为
⟨ u i , u j ⟩ = δ i j \langle u_i, u_j \rangle = \delta_{ij} ⟨ui,uj⟩=δij
其中
δ i j = { 1 当 i = j 0 当 i ≠ j \delta_{ij} = \left\{ \begin{array}{lr} 1 & 当 \,\, i =j\\ 0 & 当 \,\, i \neq j \end{array} \right. δij={10当i=j当i=j
说的是集合中任意两个向量做内积结果为 0 0 0。
规范正交基
若 B = { u 1 , u 2 , ⋯ , u k } B=\{u_1,u_2,\cdots, u_k\} B={u1,u2,⋯,uk}为一个内积空间 V V V中的规范正交集,则 B B B为子空间 S = Span ( u 1 , u 2 , ⋯ , u k ) S=\text{Span}(u_1,u_2,\cdots, u_k) S=Span(u1,u2,⋯,uk)的一组基。我们称 B B B为 S S S的一组规范正交基。
正交矩阵
定义 若一个 n × n n \times n n×n矩阵 Q Q Q的列向量构成 R n R^n Rn中的一组规范正交基,则称 Q Q Q为正交矩阵。
定理 一个 n × n n \times n n×n矩阵 Q Q Q是正交矩阵的充要条件为 Q T Q = I Q^TQ=I QTQ=I。
由定理可得,若 Q Q Q为一正交矩阵,则 Q Q Q可逆,且 Q − 1 = Q T Q^{-1}=Q^T Q−1=QT。
性质 若 Q Q Q为一个 n × n n \times n n×n的正交矩阵,则:
- Q Q Q的列向量构成了 R n R^n Rn的一组规范正交基
- Q T Q = I Q^TQ=I QTQ=I
- Q T = Q − 1 Q^T=Q^{-1} QT=Q−1
- ⟨ Q x , Q y ⟩ = ⟨ x , y ⟩ \langle Qx, Qy \rangle = \langle x, y \rangle ⟨Qx,Qy⟩=⟨x,y⟩
- ∣ ∣ Q x ∣ ∣ 2 = ∣ ∣ x ∣ ∣ 2 ||Qx||_2 = ||x||_2 ∣∣Qx∣∣2=∣∣x∣∣2
相似矩阵
正定矩阵与半正定矩阵
定义1 给定一个大小为 n × n n \times n n×n的实对称矩阵 A A A,若对于任意长度为 n n n的非零向量 x x x,有 x T A x > 0 x^TAx > 0 xTAx>0恒成立,则矩阵 A A A是一个正定矩阵。
定义2 给定一个大小为 n × n n \times n n×n的实对称矩阵 A A A,若对于任意长度为 n n n的非零向量 x x x,有 x T A x ≥ 0 x^TAx \geq 0 xTAx≥0恒成立,则矩阵 A A A是一个半正定矩阵。
向量的内积
定义1 设有 n n n为向量
x = ( x 1 x 2 ⋮ x n ) , y = ( y 1 y 2 ⋮ y n ) x = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}, \, y=\begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} x= x1x2⋮xn ,y= y1y2⋮yn
令
[ x , y ] = x 1 y 1 + x 2 y 2 + ⋯ x n y n , [x,y] =x_1y_1 + x_2y_2 + \cdots x_ny_n, [x,y]=x1y1+x2y2+⋯xnyn,
[ x , y ] [x,y] [x,y]称为向量 x x x与 y y y的内积(内积也叫点积,也可表示为 ⟨ x , y ⟩ \langle x,y \rangle ⟨x,y⟩)。
内积是两个向量之间的一种运算,其结果是一个实数,用矩阵记号表示,当 x x x与 y y y都是列向量时,有
[ x , y ] = x T y = y T x [x,y] = x^Ty = y^T x [x,y]=xTy=yTx
内积具有下列性质(其中 x , y , z x,y,z x,y,z为 n n n维向量, λ \lambda λ为实数):
- [ x , y ] = [ y , x ] [x,y] = [y,x] [x,y]=[y,x]
- [ λ x , y ] = λ [ x , y ] [\lambda x,y] = \lambda[x,y] [λx,y]=λ[x,y]
- [ x + y , z ] = [ x , z ] + [ y , z ] [x+y,z] = [x,z] + [y,z] [x+y,z]=[x,z]+[y,z]
- 当 x = 0 x=0 x=0时, [ x , x ] = 0 [x,x]=0 [x,x]=0;当 x ≠ 0 x \neq 0 x=0时, [ x , x ] > 0 [x,x] >0 [x,x]>0
可以得到柯西不等式
[ x , y ] 2 ≤ [ x , x ] [ y , y ] [x,y]^2 \leq [x,x][y,y] [x,y]2≤[x,x][y,y]
定义2 令
∣ ∣ x ∣ ∣ = [ x , ] = x 1 2 + x 2 2 + ⋯ + x n 2 ||x|| =\sqrt{[x,]} = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} ∣∣x∣∣=[x,]=x12+x22+⋯+xn2
∣ ∣ x ∣ ∣ ||x|| ∣∣x∣∣称为 n n n维向量 x x x的长度(或范数)。
当 ∣ ∣ x ∣ ∣ = 1 ||x|| =1 ∣∣x∣∣=1时,称 x x x为单位向量。
向量的长度具有以下性质:
- 非负性 当 x ≠ 0 x \neq 0 x=0时, ∣ ∣ x ∣ ∣ > 0 ||x|| >0 ∣∣x∣∣>0;当 x = 0 x =0 x=0时, ∣ ∣ x ∣ ∣ = 0 ||x|| =0 ∣∣x∣∣=0
- 齐次性 ∣ ∣ λ x ∣ ∣ = ∣ λ ∣ ∣ ∣ x ∣ ∣ ||\lambda x|| = |\lambda| ||x|| ∣∣λx∣∣=∣λ∣∣∣x∣∣
- 三角不等式 ∣ ∣ x + y ∣ ∣ ≤ ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ ||x+y|| \leq ||x|| +||y|| ∣∣x+y∣∣≤∣∣x∣∣+∣∣y∣∣
当 [ x , y ] = 0 [x,y]=0 [x,y]=0时,称向量 x x x与 y y y正交。显然,若 x = 0 x=0 x=0,则 x x x与任何向量都正交。
定理1 若 n n n维向量 a 1 , a 2 , ⋯ , a r a_1,a_2,\cdots, a_r a1,a2,⋯,ar是一组两两正交的非零向量,则 a 1 , a 2 , ⋯ , a r a_1,a_2,\cdots, a_r a1,a2,⋯,ar线性无关。
若向量 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3线性无关,则它们互相不能用其他向量线性表示。
证 设有 λ 1 , λ 2 , ⋯ , λ r \lambda_1,\lambda_2,\cdots,\lambda_r λ1,λ2,⋯,λr使
λ 1 a 1 + λ 1 a 2 + ⋯ + λ r a r = 0 , \lambda_1a_1 + \lambda_1a_2 + \cdots + \lambda_ra_r = 0, λ1a1+λ1a2+⋯+λrar=0,
我们要证明 λ 1 = λ 2 = ⋯ λ r = 0 \lambda_1 =\lambda_2 = \cdots \lambda_r = 0 λ1=λ2=⋯λr=0。以 a 1 T a_1^T a1T左乘上式两端,当 i ≥ 2 i \geq 2 i≥2时, a 1 T a i = 0 a_1^T a_i =0 a1Tai=0,要使上式等于零,所以
λ 1 a 1 T a 1 = 0 \lambda_1 a_1^T a_1 = 0 λ1a1Ta1=0
因为 a 1 ≠ 0 a_1 \neq 0 a1=0,所以 a 1 T a 1 ≠ 0 a_1^T a_1 \neq 0 a1Ta1=0,从而只能 λ 1 = 0 \lambda_1=0 λ1=0,类似可以证明 λ 2 = 0 , ⋯ , λ r = 0 \lambda_2 =0,\cdots, \lambda_r =0 λ2=0,⋯,λr=0。
于是向量组 a 1 , a 2 , ⋯ , a r a_1,a_2,\cdots, a_r a1,a2,⋯,ar线性无关。
定义3 设 n n n维向量 e 1 , e 2 , ⋯ , e r e_1,e_2,\cdots,e_r e1,e2,⋯,er是向量空间 V V V的一个基,如果 e 1 , e 2 , ⋯ , e r e_1,e_2,\cdots,e_r e1,e2,⋯,er两两正交,且都是单位向量,则称 e 1 , e 2 , ⋯ , e r e_1,e_2,\cdots,e_r e1,e2,⋯,er是 V V V的一个规范正交基。
若 e 1 , e 2 , ⋯ , e r e_1,e_2,\cdots,e_r e1,e2,⋯,er是 V V V的一个规范正交基,那么 V V V中任意向量 a a a都能由 e 1 , e 2 , ⋯ , e r e_1,e_2,\cdots,e_r e1,e2,⋯,er线性表示,设表示为
a = λ 1 e 1 + λ 2 e 2 + ⋯ + λ r e r a = \lambda_1 e_1 + \lambda_ 2e_2 + \cdots + \lambda_r e_r a=λ1e1+λ2e2+⋯+λrer
定义4 如果 n n n阶矩阵 A A A满足
A T A = E ( 即 A − 1 = A T ) A^TA = E \qquad (\text{即}A^{-1}=A^T) ATA=E(即A−1=AT)
那么称 A A A为正交矩阵,简称正交阵。
A T A = E ⇒ ∣ A T ∣ ∣ A ∣ = 1 ⇒ A 可逆 ⇒ A − 1 = A T A^TA=E \Rightarrow |A^T||A|=1 \Rightarrow A\text{可逆} \Rightarrow A^{-1}=A^T ATA=E⇒∣AT∣∣A∣=1⇒A可逆⇒A−1=AT
上式用 A A A的列向量表示,即是
( a 1 T a 2 T ⋮ a n T ) ( a 1 , a 2 , ⋯ , a n ) = E , \begin{pmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_n^T \end{pmatrix} (a_1,a_2,\cdots, a_n) =E, a1Ta2T⋮anT (a1,a2,⋯,an)=E,
因为 A T A = E A^TA=E ATA=E与 A A T = E AA^T=E AAT=E等价,所以上述结论对 A A A的行向量亦成立。
由此可见, n n n阶正交阵 A A A的 n n n个列(行)向量构成向量空间 R n R^n Rn的一个规范正交基。
方阵的特征值与特征向量
定义6 设 A A A是 n n n阶矩阵,如果数 λ \lambda λ和 n n n维非零列向量 x x x使关系式
A x = λ x (1) Ax =\lambda x \tag{1} Ax=λx(1)
成立,那么,这样的数 λ \lambda λ称为矩阵 A A A的特征值,非零向量 x x x称为 A A A的对应于特征值 λ \lambda λ的特征向量。
( 1 ) (1) (1)式也可以写成
( A − λ E ) x = 0 (A - \lambda E)x = 0 (A−λE)x=0
这是 n n n个未知数 n n n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式
∣ A − λ E ∣ = 0 , |A - \lambda E| = 0, ∣A−λE∣=0,
即
∣ a 11 − λ a 12 ⋯ a 1 n a 21 a 22 − λ ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n − λ ∣ = 0 \begin{vmatrix} a_{11} - \lambda & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} -\lambda & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} - \lambda\\ \end{vmatrix}= 0 a11−λa21⋮an1a12a22−λ⋮an2⋯⋯⋯a1na2n⋮ann−λ =0
R ( A ) = R ( A , b ) < n R(A) = R(A,b) < n R(A)=R(A,b)<n 无穷解
上式是以 λ \lambda λ为未知数的一元 n n n次方程,称为矩阵 A A A的特征方程。其左端 ∣ A − λ E ∣ |A - \lambda E| ∣A−λE∣是 λ \lambda λ的 n n n次多项式,记作 f ( λ ) f(\lambda) f(λ),称为矩阵 A A A的特征多项式。
设 n n n阶矩阵 A = ( a i j ) A = (a_{ij}) A=(aij)的特征值为 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots, \lambda_n λ1,λ2,⋯,λn,有以下性质:
- λ 1 + λ 2 + ⋯ + λ n = a 11 + a 22 + ⋯ + a n n \lambda_1 + \lambda_2 +\cdots + \lambda_n = a_{11} + a_{22} + \cdots +a_{nn} λ1+λ2+⋯+λn=a11+a22+⋯+ann
- λ 1 λ 2 ⋯ λ n = ∣ A ∣ \lambda_1\lambda_2 \cdots \lambda_n =|A| λ1λ2⋯λn=∣A∣
设 λ = λ i \lambda = \lambda_i λ=λi为矩阵 A A A的一个特征值,则由方程
( A − λ i E ) x = 0 (A - \lambda_iE)x = 0 (A−λiE)x=0
可求得非零解 x = p i x = p_i x=pi,那么 p i p_i pi便是 A A A的对应于特征值 λ i \lambda_i λi的特征向量。
例 设 λ \lambda λ是方阵 A A A的特征值,证明
- λ 2 \lambda^2 λ2是 A 2 A^2 A2的特征值
- 当 A A A可逆时, 1 λ \frac{1}{\lambda} λ1是 A − 1 A^{-1} A−1的特征值。
证 因 λ \lambda λ是 A A A的特征值,故有 x ≠ 0 x \neq 0 x=0使 A x = λ x Ax= \lambda x Ax=λx。于是
(1) A 2 x = A ( A x ) = A ( λ x ) = λ ( A x ) = λ 2 x A^2 x = A(Ax) = A(\lambda x) = \lambda(A x) = \lambda^2 x A2x=A(Ax)=A(λx)=λ(Ax)=λ2x,
所以 λ 2 \lambda^2 λ2是 A 2 A^2 A2的特征值。
依此类推,不难证明:若 λ \lambda λ是 A A A的特征值,则 λ k \lambda^k λk是 A k A^k Ak的特征值。
(2) 当 A A A可逆时,由 A x = λ x A x = \lambda x Ax=λx,有 x = λ A − 1 x x = \lambda A^{-1} x x=λA−1x,因 x ≠ 0 x \neq 0 x=0,知 λ ≠ 0 \lambda \neq 0 λ=0,故
A − 1 x = 1 λ x , A^{-1} x = \frac{1}{\lambda} x, A−1x=λ1x,
所以 1 λ \frac{1}{\lambda} λ1是 A − 1 A^{-1} A−1的特征值。
定理2 设 λ 1 , λ 2 , ⋯ , λ m \lambda_1,\lambda_2,\cdots, \lambda_m λ1,λ2,⋯,λm是方阵 A A A的 m m m个特征值, p 1 , p 2 , ⋯ , p m p_1,p_2,\cdots, p_m p1,p2,⋯,pm依次是与之对应的特征向量,如果 λ 1 , λ 2 , ⋯ , λ m \lambda_1,\lambda_2,\cdots, \lambda_m λ1,λ2,⋯,λm各不相等,则 p 1 , p 2 , ⋯ , p m p_1,p_2,\cdots, p_m p1,p2,⋯,pm线性无关。
相似矩阵
定义7 设 A , B A,B A,B都是 n n n阶矩阵,若有可逆矩阵 P P P,使
P − 1 A P = B P^{-1}AP = B P−1AP=B
则称 B B B是 A A A的相似矩阵,或说矩阵 A A A与 B B B相似。对 A A A进行运算 P − 1 A P^{-1}A P−1A称为对 A A A进行相似变换。可逆矩阵 P P P称为把 A A A变成 B B B的相似变换矩阵。
定理3 若 n n n阶矩阵 A A A与 B B B相似,则 A A A与 B B B的特征多项式相同,从而 A A A与 B B B的特征值亦相同。
证 因 A A A与 B B B相似,即有可逆矩阵 P P P,使 P − 1 A P = B P^{-1}AP=B P−1AP=B,故
∣ B − λ E ∣ = ∣ P − 1 A P − λ P − 1 P ∣ = ∣ P − 1 ( A − λ E ) P ∣ = ∣ P − 1 ∣ ⋅ ∣ A − λ E ∣ ⋅ ∣ P ∣ = ∣ A − λ E ∣ \begin{aligned} |B -\lambda E| &= |P^{-1}AP - \lambda P^{-1}P| \\ &=|P^{-1}(A-\lambda E)P| \\ &= |P^{-1}| \cdot |A - \lambda E|\cdot |P| \\ &= |A - \lambda E| \end{aligned} ∣B−λE∣=∣P−1AP−λP−1P∣=∣P−1(A−λE)P∣=∣P−1∣⋅∣A−λE∣⋅∣P∣=∣A−λE∣
推论 若 n n n阶矩阵 A A A与对角阵
Λ = [ λ 1 λ 2 ⋱ λ n ] \Lambda= \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & & \lambda_n\\ \end{bmatrix} Λ= λ1λ2⋱λn
相似,则 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn即是 A A A的 n n n个特征值。
下面我们要讨论的主要问题是:对 n n n阶矩阵 A A A,寻求相似变换矩阵 P P P,使 P − 1 A P = Λ P^{-1}AP = \Lambda P−1AP=Λ为对角阵,这就称为把矩阵 A A A对角化。
假设已经找到可逆矩阵 P P P,使 P − 1 A P = Λ P^{-1}AP=\Lambda P−1AP=Λ为对角阵,我们来讨论 P P P应满足什么关系。
把 P P P用其列向量表示为
P = ( p 1 , p 2 , ⋯ , p n ) , P=(p_1,p_2,\cdots,p_n), P=(p1,p2,⋯,pn),
由 P − 1 A P = Λ P^{-1}AP=\Lambda P−1AP=Λ,得 A P = P Λ AP=P\Lambda AP=PΛ,即
A ( p 1 , p 2 , ⋯ , p n ) = ( p 1 , p 2 , ⋯ , p n ) [ λ 1 λ 2 ⋱ λ n ] = ( λ 1 p 1 , λ 2 p 2 , ⋯ , λ n p n ) , \begin{aligned} A(p_1,p_2,\cdots,p_n) &= (p_1,p_2,\cdots,p_n)\begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & & \lambda_n\\ \end{bmatrix} \\ &= (\lambda_1p_1,\lambda_2p_2,\cdots, \lambda_np_n), \end{aligned} A(p1,p2,⋯,pn)=(p1,p2,⋯,pn) λ1λ2⋱λn =(λ1p1,λ2p2,⋯,λnpn),
于是有
A p i = λ i p i ( i = 1 , 2 , ⋯ , n ) . Ap_i = \lambda_ip_i\qquad(i=1,2,\cdots,n). Api=λipi(i=1,2,⋯,n).
可见 λ i \lambda_i λi是 A A A的特征值,而 P P P的列向量 p i p_i pi就是 A A A的对应于特征值 λ i \lambda_i λi的特征向量。
定理4 n n n阶矩阵 A A A与对角阵相似(即 A A A能对角化)的充分必要条件是 A A A有 n n n个线性无关的特征向量。
联系定理2,得
对称矩阵的对角化
定理5 对称阵的特征值为实数
证 设复数 λ \lambda λ为对称阵 A A A的特征值,复向量 x x x为对应的特征向量,即 A x = λ x , x ≠ 0 Ax=\lambda x,x \neq 0 Ax=λx,x=0。
用 λ ‾ \overline{\lambda} λ表示 λ \lambda λ的共轭复数, x ‾ \overline{x} x表示 x x x的共轭复向量,而 A A A为实矩阵,有 A = A ‾ A = \overline{A} A=A,故
A x ‾ = A ‾ x ‾ = ( A x ‾ ) = ( λ x ‾ ) = λ ‾ x ‾ A\overline{x} = \overline{A}\overline{x} = (\overline{Ax}) = (\overline{\lambda x}) = \overline{\lambda}\overline{x} Ax=Ax=(Ax)=(λx)=λx。于是有
x ‾ T A x = x ‾ T ( A x ) = x ‾ T λ x = λ x ‾ T x , \overline{x}^TAx = \overline{x}^T(Ax)=\overline{x}^T \lambda x=\lambda \overline{x}^T x, xTAx=xT(Ax)=xTλx=λxTx,
及
x ‾ T A x = ( x ‾ T A T ) x = ( A x ‾ ) T x = ( λ ‾ x ‾ ) T x = λ ‾ x ‾ T x , \overline{x}^TAx = (\overline{x}^TA^T)x=(A\overline{x})^Tx=(\overline{\lambda}\overline{x})^Tx=\overline{\lambda}\overline{x}^Tx, xTAx=(xTAT)x=(Ax)Tx=(λx)Tx=λxTx,
两式相减,得
( λ − λ ‾ ) x ‾ T x = 0 , (\lambda - \overline{\lambda})\overline{x}^Tx = 0, (λ−λ)xTx=0,
因 x ≠ 0 x \neq 0 x=0,所以
x ‾ T x = ∑ i = 1 x ‾ i x i = ∑ i = 1 ∣ x i ∣ 2 ≠ 0 , \overline{x}^Tx=\sum_{i=1}\overline{x}_i x_i = \sum_{i=1} |x_i|^2 \neq 0, xTx=i=1∑xixi=i=1∑∣xi∣2=0,
故 λ − λ ‾ = 0 \lambda -\overline{\lambda} =0 λ−λ=0,即 λ = λ ‾ \lambda = \overline{\lambda} λ=λ,说明 λ \lambda λ是实数。
定理6 设 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2是对称阵 A A A的两个特征值, p 1 , p 2 p_1,p_2 p1,p2是对应的特征向量。若 λ 1 ≠ λ 2 \lambda_1 \neq \lambda_2 λ1=λ2,则 p 1 , p 2 p_1,p_2 p1,p2正交。
证 λ 1 p 1 = A p 1 , λ 2 p 2 = A p 2 , λ 1 ≠ λ 2 \lambda_1p_1 = Ap_1,\lambda_2p_2 = Ap_2,\lambda_1 \neq \lambda_2 λ1p1=Ap1,λ2p2=Ap2,λ1=λ2。
因 A A A对称,故 λ 1 p 1 T = ( λ 1 p 1 ) T = ( A p 1 ) T = p 1 T A T = p 1 T A \lambda_1p_1^T=(\lambda_1p_1)^T=(Ap_1)^T=p_1^TA^T=p_1^TA λ1p1T=(λ1p1)T=(Ap1)T=p1TAT=p1TA,于是
λ 1 p 1 T p 2 = p 1 T A p 2 = p 1 T ( λ 2 p 2 ) = λ 2 p 1 T p 2 , \lambda_1p_1^Tp_2 = p_1^TAp_2=p_1^T(\lambda_2p_2)=\lambda_2p_1^Tp_2, λ1p1Tp2=p1TAp2=p1T(λ2p2)=λ2p1Tp2,
即
( λ 1 − λ 2 ) p 1 T p 2 = 0. (\lambda_1 -\lambda_2)p_1^Tp_2 = 0. (λ1−λ2)p1Tp2=0.
因为 λ 1 ≠ λ 2 \lambda_1 \neq \lambda_2 λ1=λ2,故 p 1 T p 2 = 0 p_1^Tp_2=0 p1Tp2=0,即 p 1 , p 2 p_1,p_2 p1,p2正交。
定理7 设 A A A是 n n n阶对称阵,则必有正交阵 P P P,使 P − 1 A P = P T A P = Λ P^{-1}AP=P^TAP=\Lambda P−1AP=PTAP=Λ,其中 Λ \Lambda Λ是以 A A A的 n n n个特征值为对角元的对角阵。
推论 设 A A A为 n n n阶对称阵, λ \lambda λ是 A A A的特征方程的 k k k重根,则矩阵 A − λ E A -\lambda E A−λE的秩 R ( A − λ E ) = n − k R(A -\lambda E)= n -k R(A−λE)=n−k,从而对应特征值 λ \lambda λ恰有 k k k个线性无关的特征向量。
二次型及其标准形
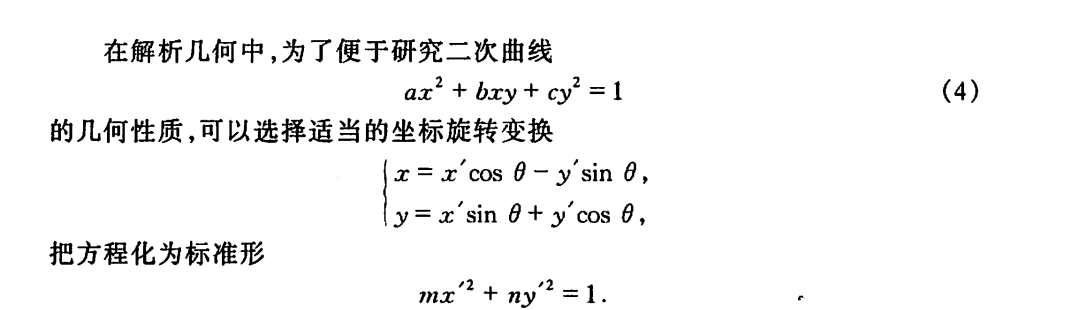

使二次型只含平方项,也就是用 ( 7 ) (7) (7)带入 ( 5 ) (5) (5),能使
f = k 1 y 1 2 + k 2 y 2 2 + ⋯ + k n y n 2 , f = k_1y^2_1 + k_2y_2^2 + \cdots + k_ny_n^2, f=k1y12+k2y22+⋯+knyn2,
这种只含平方项的二次型,称为二次型的标形型(或法式)。
如果标准形的系数 k 1 , k 2 , ⋯ , k n k_1,k_2,\cdots,k_n k1,k2,⋯,kn只在 1 , − 1 , 0 1,-1,0 1,−1,0三个数中取值,也就是用 ( 7 ) (7) (7)代入 ( 5 ) (5) (5),能使
f = y 1 2 + ⋯ + y p 2 − y p + 1 2 − ⋯ − y r 2 , f = y_1^2 + \cdots + y_p^2 - y^2_{p+1} - \cdots - y^2_r, f=y12+⋯+yp2−yp+12−⋯−yr2,
则称上式为二次型的规范形。

则二次型可记作
f = x T A x , (8) f = x^TAx, \tag{8} f=xTAx,(8)
其中 A A A为对称阵。
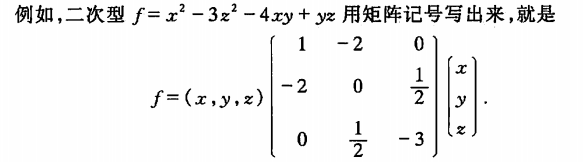

如果 f ( x ) ≥ 0 f(x) \geq 0 f(x)≥0,则是半正定。
更新记录
- 2021-05-25 补充单位矩阵、奇异矩阵
- 2021-05-26 新增标准基、正交性
- 2021-05-27 新增特征值
- 2021-06-05 新增实对称矩阵定理
- 2021-06-19 新值行列式
参考
- 《线性代数》 利昂著
- 《线性代数》 同济大学第五版
- 维基百科
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!