算法设计与分析_练习一_递推算法
目录
01:猴子吃桃
02:递归:爬楼梯
03:递归:Pell数列
04:过河卒
05:昆虫繁殖
01:猴子吃桃
描述
猴子第一天摘下若干个桃子,当即吃了一半,好不过瘾,又多吃了一个。第二天早上又吃了剩下的桃子的一半,又多吃了一个。以后每天都吃了前一天剩下的一半零一个,到第10 天早上想再吃的时候,就剩下一个桃子。求第一天共摘多少个桃子。
输入
无
输出
第一天摘的桃子数
样例输入
无
样例输出
1534
#include
using namespace std;int main() {int f[11];f[10] = 1;for(int i = 9; i >= 1; i--) {f[i] = 2 * (f[i + 1] + 1);}cout << f [1];
}
02:递归:爬楼梯
描述
小明爬楼梯,他可以每次走1级或者2级,输入楼梯的级数,求不同的走法数。
例如:楼梯一共有3级,他可以每次都走一级,或者第一次走一级,第二次走两级;也可以第一次走两级,第二次走一级,一共3种方法。
输入
输入包含若干行正整数,第一行正整数K代表数据组数;后面K行,每行包含一个正整数N,代表楼梯级数,1 <= N <= 30
输出
不同的走法数,每一行输入对应一行输出
样例输入
3
5
8
10
样例输出
8
34
89
#include
using namespace std;int main() {int K, i, j;cin >> K;for(i = 0; i < K; i++) {int N;cin >> N;int f[31];f[1] = 1;f[2] = 2; //边界条件for(j = 3; j <= N; j++) { //递推过程f[j] = f[j - 1] + f[j - 2];}cout << f[N] << endl;}
}
03:递归:Pell数列
描述
Pell数列,
,
, ...的定义是这样的,
= 1,
= 2, ... ,
=2 *
+
(n > 2)。
给出一个正整数k,要求Pell数列的第k项模上32767是多少。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数k (1 ≤ k < 30),代表Pell数列的第k项。
输出
n行,每行输出Pell数列的第k项模上32767的值。
样例输入
2
1
8
样例输出
1
408
#include
using namespace std;int main() {int n, i, j;cin >> n;for(i = 0; i < n; i++) {int k;cin >> k;int Pell[31];Pell[1] = 1; Pell[2] = 2; //边界条件for(j = 3; j <= k; j++) { //递推过程Pell[j] = (2 * Pell[j - 1] + Pell[j - 2]) % 32767;}cout << Pell[k] << endl;}
}
04:过河卒
描述
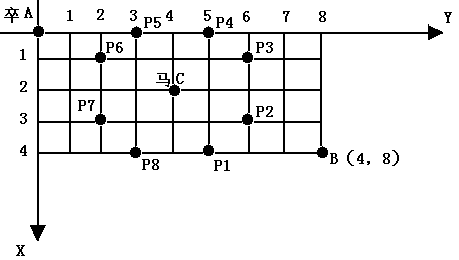
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上的某一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点,如图3-1中的C点和P1,……,P8,卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的,C≠A且C≠B。
现在要求你计算出卒从A点能够到达B点的路径的条数。
输入
B点的坐标(n,m)以及对方马的坐标(X,Y)
输出
从A点能够到达B点的路径的条数。
样例输入
6 6 3 2
样例输出
17
#include
#include
using namespace std;//协助计算马所能到达点
int fx[9] = {0, -2, -1, 1, 2, 2, 1, -1, -2}, fy[9] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
int B_x, B_y, mx, my;
long long ans;
long long f[30][30];
bool v[30][30]; // 标记马的控制点
int main() {cin >> B_x >> B_y >> mx >> my;B_x++;B_y++;mx++;my++;//设置原点的路径数为1f[1][1] = 1;//标记马所能走到的点 v[mx][my] = 1;for(int i = 1; i <= 8; i++)v[mx + fx[i]][my + fy[i]] = 1;for(int i = 1; i <= B_x; i++)for(int j = 1; j <= B_y; j++) {//如果是马能走到的点,则跳过此次循环if(v[i][j]) continue;//如果不是,则将能到达该点的路径数赋值为能到达它左边那点的路径数和能到达它上面那点的路径数之和f[i][j] = max(f[i][j], f[i - 1][j] + f[i][j - 1]);}//最终输出能到达B点的路径数cout << f[B_x][B_y];return 0;
} 05:昆虫繁殖
描述
科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵,每对卵要过两个月长成成虫。
假设每个成虫不死,第一个月只有1成虫,且卵长成成虫后的第一个月不产卵(过X个月产卵),问过Z个月以后,共有成虫多少对?
输入
x,y,z的数值
输出
过Z个月以后,共有成虫数
样例输入
1 2 8
样例输出
37
#include
using namespace std;int main() {long long x, y, z, f[101]={0}, b[101]={0}, i, j;cin >> x >> y >> z;for(i = 1; i <= x; i++) { // 第1个月只有1成虫f[i] = 1;b[i] = 0;}for(j = x + 1; j <=z + 1; j++) { // z个月后所以求到z+1b[j] = f[j - x] * y; // 成虫经过x月产卵y个f[j] = f[j - 1] + b[j - 2]; // 卵经过2个月长成成虫}cout << f[z + 1] << endl;
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!