仿真题3.17

这道题基本按照课后习题解答的步骤来即可，没有需要改动的地方。

% 3.17(1)
N = 32;
noise = (randn(1,N) + 1i * randn(1,N))/sqrt(2);f1 = 0.15;
f2 = 0.17;
f3 = 0.26;SNR1 = 30;
SNR2 = 30;
SNR3 = 27;A1 = 10^(SNR1/20);
A2 = 10^(SNR2/20);
A3 = 10^(SNR3/20);signal1 = A1 * exp(1i*2*pi*f1*(0:N-1));
signal2 = A2 * exp(1i*2*pi*f2*(0:N-1));
signal3 = A3 * exp(1i*2*pi*f3*(0:N-1));un = signal1 + signal2 + signal3 + noise;% 基于FFT的自相关函数快速计算方法
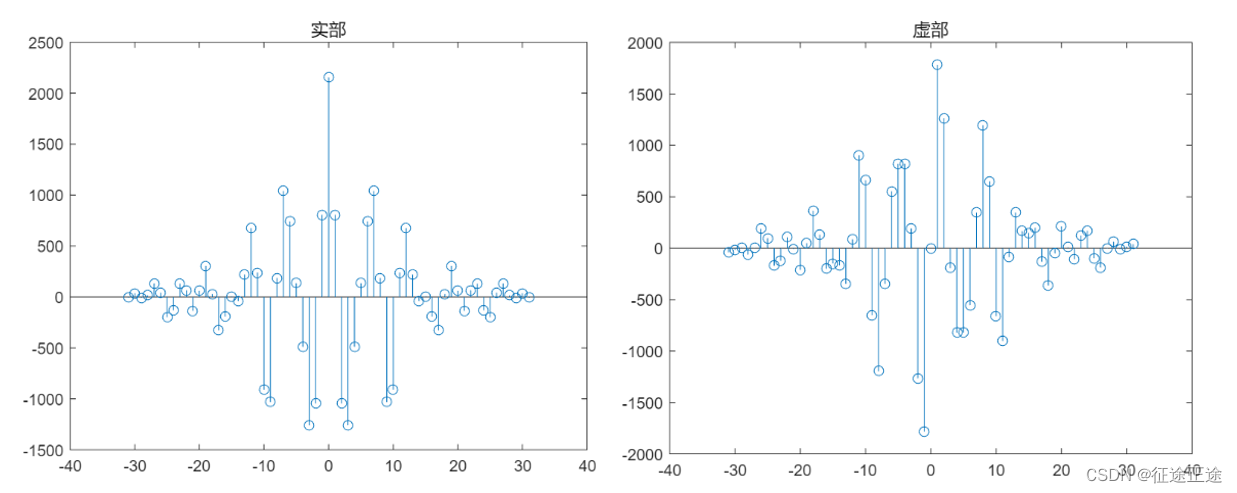
Uk = fft(un,2*N);
Sk = (1/N) * abs(Uk).^2;
r0 = ifft(Sk);
r1 = [r0(N+2:2*N),r0(1:N)];
stem(-31:1:31,real(r1));
title('实部');
stem(-31:1:31,imag(r1));
title('虚部');% 基于教材(3.1.2)估计自相关函数
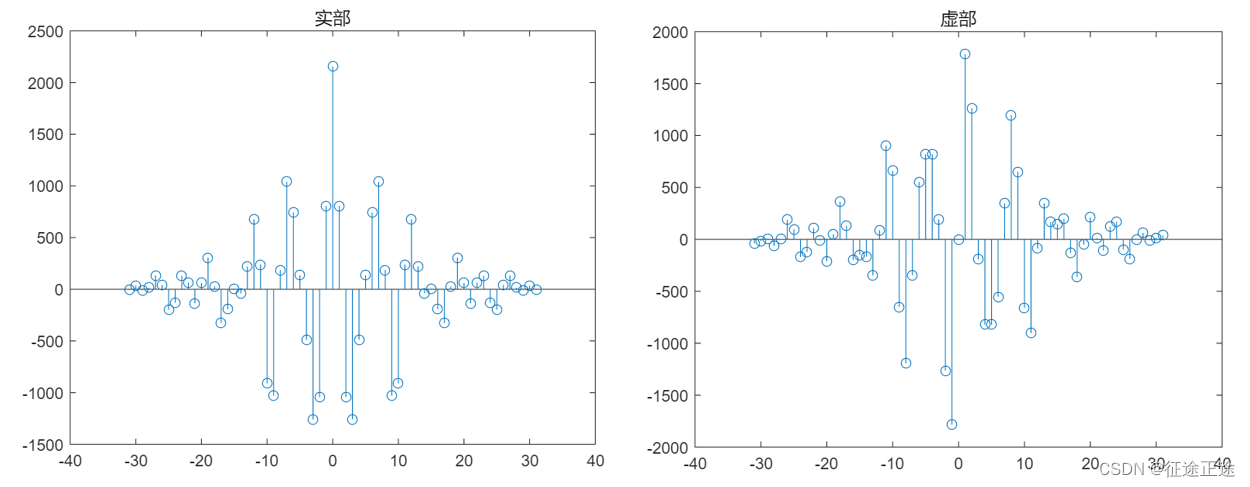
r = xcorr(un,N-1,'biased');
stem(-31:1:31,real(r));
title('实部');
stem(-31:1:31,imag(r));
title('虚部');% 3.17(2)
N = 256;
noise = (randn(1,N) + 1i * randn(1,N))/sqrt(2);f1 = 0.15;
f2 = 0.17;
f3 = 0.26;SNR1 = 30;
SNR2 = 30;
SNR3 = 27;A1 = 10^(SNR1/20);
A2 = 10^(SNR2/20);
A3 = 10^(SNR3/20);signal1 = A1 * exp(1i*2*pi*f1*(0:N-1));
signal2 = A2 * exp(1i*2*pi*f2*(0:N-1));
signal3 = A3 * exp(1i*2*pi*f3*(0:N-1));un = signal1 + signal2 + signal3 + noise;% 周期图法
NF = 1024;
Spr = fftshift((1/NF) * abs(fft(un,NF)) .^2);
Spr_db = 10*log10(Spr/max(Spr));% 归一化功率谱
w = -(NF-1)/(2*NF) : 1/NF : (NF-1)/(2*NF); % 保证0~1之间有1024个数，1023个间隔plot(w,Spr_db);
axis([-0.5 0.5 -50 0]);
xlabel('{\it \omega}/2{\pi}');
ylabel('归一化功率谱/dB');
title('周期图法');% BT法
M = 64;
r = xcorr(un,M,'biased');
NF = 1024;
BT = fftshift(fft(r,NF));BT_db = 10*log10(abs(BT)/max(abs(BT)));
plot(w,BT_db);
axis([-0.5 0.5 -40 0]);
xlabel('{\it {\omega}/2{\pi}}');
ylabel('归一化功率谱/dB');
title('BT法');% 3.17(3)
N = 256;
noise = (randn(1,N) + 1i * randn(1,N))/sqrt(2);f1 = 0.15;
f2 = 0.17;
f3 = 0.26;SNR1 = 30;
SNR2 = 30;
SNR3 = 27;A1 = 10^(SNR1/20);
A2 = 10^(SNR2/20);
A3 = 10^(SNR3/20);signal1 = A1 * exp(1i*2*pi*f1*(0:N-1));
signal2 = A2 * exp(1i*2*pi*f2*(0:N-1));
signal3 = A3 * exp(1i*2*pi*f3*(0:N-1));un = signal1 + signal2 + signal3 + noise;p = 16;
r0 = xcorr(un,p,'biased');
r = r0(p+1:2*p+1);
a(1,1) = -r(2)/r(1);
sigma(1) = r(1) - (abs(r(2))^2)/r(1);for m = 2:pk(m) = - ( r(m+1) + sum( a(m-1,1:m-1) .* r(m:-1:2)) )/sigma(m-1);a(m,m) = k(m);for i = 1:m-1a(m,i) = a(m-1,i) + k(m) * conj(a(m-1,m-i));endsigma(m) = sigma(m-1) * (1-abs(k(m))^2);
endNF = 1024;
Par = sigma(p) ./fftshift(abs(fft([1,a(p,:)],NF)) .^2);
Par_db = 10*log10(abs(Par)/max(abs(Par)));
plot(w,Par_db);
axis([-0.5 0.5 -50 0]);
xlabel('{\it {\omega}/2{\pi}}');
ylabel('归一化功率谱/dB');
title('16阶AR模型功率谱估计');

仿真题3.20

N = 1000;
noise = (randn(1,N) + 1i * randn(1,N))/sqrt(2);signal1 = exp(1i * 0.5 * pi * (0:N-1) + 1i * 2 * pi * rand);
signal2 = exp(-1i * 0.3 * pi * (0:N-1) + 1i * 2 * pi * rand);
un = signal1 + signal2 + noise;M = 8;
for k = 1:N-Mxs(:,k) = un(k+M-1:-1:k).';
end
R = xs * xs'/(N-M);% MVDR
NF = 2048;
for n = 1:NFAq = exp(-1i * 2 * pi * (n-1) / NF * (0:M-1)');Pmdvr(n) = 1/(Aq' * inv(R) * Aq);
end
Pmdvr_db = 10*log10(abs(Pmdvr)/max(abs(Pmdvr)));
w = -(NF-1)/(2*NF) : 1/NF : (NF-1)/(2*NF);
plot(w,Pmdvr_db);
axis([-0.5 0.5 -12 0]);
xlabel('{\it {\omega}/2{\pi}}');
ylabel('归一化功率谱/dB');
title('MVDR谱估计');
% 320
N=1000;%信号样本数
noise = (randn(1,N) + 1i * randn(1,N))/sqrt(2);signal1 = exp(1i * 0.5 * pi * (0:N-1) + 1i * 2 * pi * rand);
signal2 = exp(-1i * 0.3 * pi * (0:N-1) + 1i * 2 * pi * rand);
s = signal1 + signal2 + noise;
M=8;%自相关矩阵的阶数
for i=1:N-Mxx(:,i)=s(i+M-1:-1:i).';  %构造样本矩阵
end
R=xx*xx'/(N-M);%自相关矩阵
[EV,D]=eig(R);%特征值分解 
EVA=diag(D)';
[EVA,I]=sort(EVA);%特征值从小到大排序
EVA=fliplr(EVA);%左右翻转，从大到小排序
EV=fliplr(EV(:,I));%对应特征矢量排列
G=EV(:,3:M); %噪声子空间
NF=2048;%MUSIC算法
w=linspace(-pi,pi,NF);
for ii=1:NFa=exp(-1j*w(ii)*(0:M-1)');Pmusic(ii)=1/(a'*G*G'*a);
end
Pmusic=abs(Pmusic)/max(abs(Pmusic));
plot(w/2/pi,10*log10(Pmusic));
xlabel('{\it {\omega}/2{\pi}}');
ylabel('归一化功率谱 (dB)')
title('MUSIC算法');%root—music算法
GG=G*G';
co=zeros(2*M-1,1);%初始化3.6.38的2*（M-1)次方程的系数
for m=1:Mco(m:m+M-1)=co(m:m+M-1)+GG(M:-1:1,m);%计算3.6.38左边的多项式系数
end
% Prootmusic=abs(co)/max(abs(co));
% plot(10*log10(Prootmusic));
% xlabel('{\it {\omega}/2{\pi}}');
% ylabel('归一化功率谱 (dB)')
% title('ROOT-MUSIC算法');z=roots(co);%多项式求根
ph=angle(z)/(2*pi);%归一化频率
err=abs(abs(z)-1);%求2（M-1)个根与单位圆之间的距离
[err1,I]=sort(err);%将距离误差从小到大排序构成一个列向量
f=[ph(I(1)),ph(I(3))];%选择误差最小的二个值所对应的归一化频率
zz=[z(I(1)),z(I(3))];
ff=sort(f);disp(['   最接近单位圆的根为: ',num2str(zz)])
disp(['   对应的归一化频率分别为: ',num2str(ff)])% Music
w=linspace(-pi,pi,NF);
for ii=1:NFa=exp(-1j*w(ii)*(0:M-1)');Pmusic(ii)=1/(a'*G*G'*a);
end
Pmusic=abs(Pmusic)/max(abs(Pmusic));
plot(w/2/pi,10*log10(Pmusic));
xlabel('{\it {\omega}/2{\pi}}');
ylabel('归一化功率谱 (dB)')
title('MUSIC算法');% root-Music[U,E] = svd(R);
G = U(:,3:M);
Gr = G*G';
co = zeros(2*M-1,1);
for m = 1:Mco(m:m+M-1) = co(m:m+M-1) + Gr(M:-1:1,m);
end
z = roots(co);
ph = angle(z)/(2*pi);
err = abs(abs(z) - 1);
[err1,I]=sort(err);%将距离误差从小到大排序构成一个列向量
f=[ph(I(1)),ph(I(3))];%选择误差最小的二个值所对应的归一化频率
zz=[z(I(1)),z(I(3))];
ff=sort(f);

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！