Github地址

1. 实验目标概述

本次实验通过求解三个问题，训练基本 Java 编程技能，能够利用 Java OO 开发基本的功能模块，能够阅读理解已有代码框架并根据功能需求补全代码，能够为所开发的代码编写基本的测试程序并完成测试，初步保证所开发代码的正确性。另一方面，利用 Git 作为代码配置管理的工具，学会 Git 的基本使用方法。

• 基本的 Java OO 编程

• 基于 Eclipse IDE 进行 Java 编程

• 基于 JUnit 的测试

• 基于 Git 的代码配置管理

2. 实验环境配置

1. 下载安装eclipse

2. 下载安装JDK
   原先安装的是jdk13，在命令行工具中编译运行java程序时可以直接使用java 直接运行，后又安装jdk8，由于版本之间的差异，继续使用原来的命令运行时发现会有错误：找不到或无法加载主类。
   解决方式：使用javac 和java 分别进行编译和运行。

3. 下载安装git

3. 实验过程

3.1. Magic Squares

实验目的是编写isLegalMagicSquare()方法判断一个n×n的矩阵是不是一个Magic Square，如果是，返回true，如果不是，返回false。然后完善给定的generateMagicSquare()方法。

3.1.1. isLegalMagicSquare()

先读入一行数据，然后以这行的数据个数创建方阵。如果没有数据，则提示空文件，并返回false。

String myLine;
String[] list;
if(input.hasNextLine()) {myLine= input.nextLine();list = myLine.split("\t");
}
else {System.out.print("空文件输入 ");input.close();return false;
}

然后循环读入整个矩阵，如果读入过程中抛出NumberFormatException异常，说明数据格式不符合要求，可能有负数、小数等异常数据，也可能是未按要求用\t分割造成的，所以输出提示信息并返回false即可；如果读入过程中抛出ArrayIndexOutOfBoundsException异常，说明当创建的矩阵被填满时还有未读入的数据，造成在继续读入数据到矩阵时访问数组越界，原因是矩阵列数小于行数造成矩阵创建过小，这时输出提示信息并返回false即可。

catch (NumberFormatException ex) {System.out.print("含有非正整数或未用\"\\t\"分割  ");return false;
} catch(ArrayIndexOutOfBoundsException ex) { //列数小于行数造成数组越界System.out.print("行列数不相等 ");return false;
}

如果正常读入但最后控制行数的循环变量不等于最后一行的下标说明矩阵行数小于列数，同样输出输出提示信息并返回false。

if(i != length-1) { //行数小于列数System.out.print("行列数不相等 ");return false;
}

如果以上部分代码正常运行，说明输入的矩阵没有格式错误，然后只需要判断各行和与各列和以及两个对角线的和是否都相等，如果都相等说明读入的矩阵是一个Magic Square，返回true；否则输出输出提示信息并返回false。

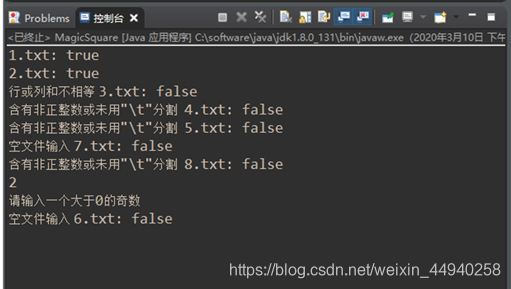
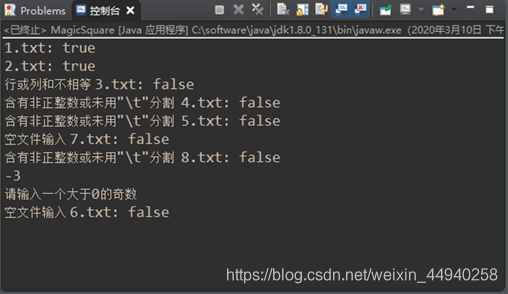
运行结果：其中使用的7.txt为空，8.txt中为中英文混杂

输入偶数生成幻方：

输入负数生成幻方：

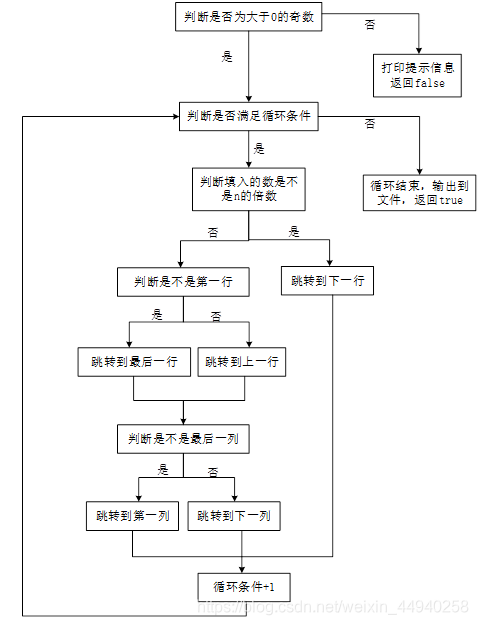
3.1.2 generateMagicSquare()

该方法根据传入的参数n确定一个大小为n×n的方阵，然后根据以下的规则把2------n填入这个方阵：

（1）将1放在第一行的正中；

（2）将后一个元素放在上一个元素的右上位置；

（3）如果上一个元素在第一行（或最后一列），那么把后一个元素放在最后一行（或第一列），而列（或行）仍为原来右上位置所在列（或行）；

（4）如果按照以上规则确定的位置已被占用，那么把后一个元素放在上一个元素的正下方，即同列的下一行

该方法的流程图如下：

3.2. Turtle Graphics

根据MIT的实验要求和代码注释，完成TurtleSoup.java中待实现的方法，实现一个叫Turtle的绘图工具并用其进行创作。

Problem 1: Clone and import

访问实验手册给出的URL地址，下载实验P2所需的代码。

在本地创建文件夹git，在文件夹下创建目录Lab1，在Lab1中打开git Bash：

使用命令git init创建Lab1的仓库。

使用git add 将文件添加到仓库的缓存区；

使用git commit -m "message"命令将缓存区的文件提交到git仓库。

使用git remote add origin 将本地仓库与Github的远程仓库链接；

使用git push -u origin master命令将本地仓库推送到Github的仓库上。

Problem 3: Turtle graphics and drawSquare

给定两个方法：forward(units)和turn(degrees)，使用这两个方法实现drawSquare(Turtle turtle, int sideLength)方法，只需要前进sideLength长度，转过90°重复这个过程四次即可。

/*** Draw a square.* * @param turtle the turtle context* @param sideLength length of each side*/
public static void drawSquare(Turtle turtle, int sideLength) {for(int i=0; i<4; i++) {turtle.forward(sideLength);turtle.turn(90);}
}

Problem 5: Drawing polygons

实现calculateRegularPolygonAngle，计算正多边形内角，利用正多边形边数和内角的公式计算：(sides - 2) * 180.00 / sides。

实现drawRegularPolygon，调用已实现的caculateRegulaerPolygonAngle函数计算正多边形的内角，由于需要的是转过的角度，再用180减去内角大小，然后调用turtle.forward和turtle.turn实现即可。

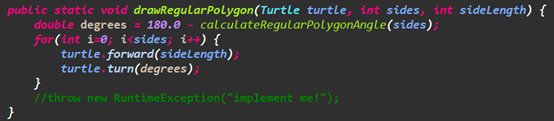
/*** Given the number of sides, draw a regular polygon.* (0,0) is the lower-left corner of the polygon; use only right-hand turns to draw.* * @param turtle the turtle context* @param sides number of sides of the polygon to draw* @param sideLength length of each side*/
public static void drawRegularPolygon(Turtle turtle, int sides, int sideLength) {double degrees = 180.0 - calculateRegularPolygonAngle(sides);for(int i=0; i<sides; i++) {turtle.forward(sideLength);turtle.turn(degrees);}
}

运行结果：

画一个正17边形

Problem 6: Calculating Bearings

实现calculateBearingToPoint，计算以现在的方向从当前位置到目标位置需要转过的角度，即当前点到目标点的向量和当前方向向量之间的夹角。

由两个点的坐标计算夹角的正切值 (targetY-currentY) / (targetX-currentX)，然后调用Math类的静态反三角函数方法Math.atan得到弧度值，然后除以Math.PI乘以180得到角度大小，如果得到的角度是负值，需要将其加360°转换为正值。然后判断当前的角度是否小于90°，小于就可以直接转换为极坐标下的极角，如果大于，就需要在计算后的值上加360°转换为正值。通过以上的转换，我们成功的把角度转换到了极坐标下，然后就可以直接相减得到需要转过的角度，而当结果是负值时同样需要加360°转换为正值。

public static double calculateBearingToPoint(double currentBearing, int currentX, int currentY,int targetX, int targetY) {double targetBearing = Math.atan((double)(targetY-currentY) / (targetX-currentX)) / Math.PI * 180.0;if(targetBearing < 0) targetBearing += 360.0;if(currentBearing <= 90)currentBearing = 90 - currentBearing;else currentBearing =  360 + 90 - currentBearing;if(targetBearing > currentBearing)return 360.0 + currentBearing - targetBearing;else return currentBearing - targetBearing;}

实现calculateBearings，目的是计算从第一个点开始，每次到下一个点需要转过的角度。只需要调用calculateBearingToPoint方法计算即可。

Problem 7: Convex Hulls

实现convexHull，如果点集中的点数小于3时，直接返回原点集即可。否则，先找出这个点集中最左的点，即横坐标最小，然后使用向量的外积寻找以这个点到下一个逆时针转过角度最大的点，然后以下一个点为起点继续寻找，直到找到的点是最开始的起点，返回所经过的点集即可。

下图所示部分代码为寻找某个点为起点，判断其他点，如果ans小于零，说明到i这个点比到q这个点逆时针转过的角度更大，所以更新q=i。

for(int i=0; i<pointsArray.length; i++) {double ans = (pointsArray[i].y() - pointsArray[p].y()) * (pointsArray[q].x() - pointsArray[i].x())- (pointsArray[i].x() - pointsArray[p].x()) * (pointsArray[q].y() - pointsArray[i].y());if(ans < 0) q = i;
}

Problem 8: Personal art

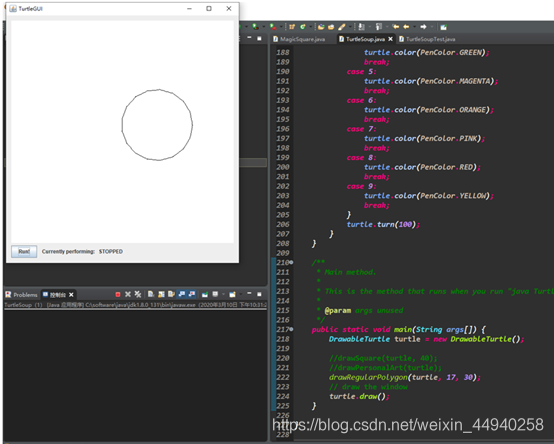
要求设计实现绘制一个图形，通过控制每次转过的角度和前进的长度绘制了以下图形。

实现：通过一千次循环，由于直接以循环变量为步长的效果过大，线条过于疏散，把步长缩短为原来的1/3，然后每次以循环变量的百位为判断标准，确定下一次画笔颜色，最后调整前进方向，转过100°，进入下一次循环。

public static void drawPersonalArt(Turtle turtle) {for (int i = 0; i < 1000; i++) {turtle.forward(i/3);	//缩短每步的步长switch((i/100)%10) {case 0:	turtle.color(PenColor.BLACK); break;case 1: turtle.color(PenColor.GRAY); break;case 2: turtle.color(PenColor.BLUE); break;case 3: turtle.color(PenColor.CYAN); break;case 4: turtle.color(PenColor.GREEN); break;case 5: turtle.color(PenColor.MAGENTA); break;case 6: turtle.color(PenColor.ORANGE); break;case 7: turtle.color(PenColor.PINK); break;case 8: turtle.color(PenColor.RED); break;case 9: turtle.color(PenColor.YELLOW); break;}turtle.turn(100);}
}

3.3. Social Network

实现Person和FriendshipGraph两个类，模拟社交网络，提供添加节点以及节点之间添加边，通过BFS计算两节点之间最短路的功能。

3.3.1. 设计/实现FriendshipGraph类

一共要求实现三个方法：addVertex向社交网络中添加新的节点(人)，addEdge向社交网络中添加新的边(社交关系)，getDistance用来求两个点之间的最短距离。

由于要保存所有的点，所以定义了一个List personList来保存所有的人。

addVertex：在社交网络中，根据要求，每个人由唯一的名字，所以在将新的点加入personList之前要先检查这个人的名字是否在之前已经出现过，如果出现过，打印提示信息并结束程序的运行，如果没有，将这个人加入personList中。

for(Person p:personList) {if(p.getName().equals(person.getName())) {System.out.println("Name repetition!!!");System.exit(0);}
}

addEdge：调用第一个人的addFriend方法将第二个人加入到第一个人的朋友的集合中。

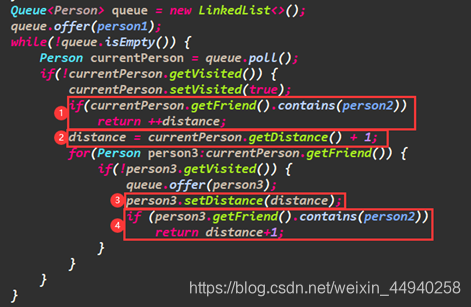
getDistance：先判斷person1和person2是不是同一个人，如果是，直接返回距离为0；如果不是再继续进行下去，然后就是一个BFS算法，根据需要增加了计算距离的功能。①位置是person2是currentPerson的朋友，只要把当前distance加一返回就可以了。②位置是重新设置distance为currentPerson的距离加一，代表currentPerson的朋友到person1的距离，然后在③处设置currentPerson的每一个朋友的distance。④处判断的是person2是不是currentPerson的朋友的朋友，如果是返回currentPerson的朋友的distance+1即可。

3.3.2. 设计/实现Person类

3.3.2.1. 存储数据结构

private String name;------保存Person的名字

private boolean visited;------标识这个Person在BFS中是否已经被访问过

private Set friend;------这个Person所有的朋友

private int distance;------保存在getDistance中所到达的距离

3.3.2.2. 内部方法实现

由于所定义的数据结构全都是私有的，所以定义了相应的get和set方法：

GetName：获得这个Person的名字；

getVisited：获得访问状态；

setVisited：设置访问状态；

getFriend：获得这个Person所有的朋友；

addFriend：为这个Person添加新的朋友，用于FriendshipGraph类中添加边；

getDistance：获得这个Person的距离；

setDistance：设置这个Person的距离。

通过这些方法就可以对Person类中私有的数据进行访问。

3.3.3. 设计/实现客户端代码main()

客户端代码：

public static void main(String[] args) {FriendshipGraph graph = new FriendshipGraph();Person rachel = new Person("Rachel");Person ross = new Person("Ross");Person ben = new Person("Ben");Person kramer = new Person("Kramer");graph.addVertex(rachel);graph.addVertex(ross);graph.addVertex(ben);graph.addVertex(kramer);graph.addEdge(rachel, ross);graph.addEdge(ross, rachel);graph.addEdge(ross, ben);graph.addEdge(ben, ross);System.out.println(graph.getDistance(rachel, ross)); // should print 1System.out.println(graph.getDistance(rachel, ben)); // should print 2System.out.println(graph.getDistance(rachel, rachel)); // should print 0System.out.println(graph.getDistance(rachel, kramer)); // should print -1
}

3.3.4. 设计/实现测试用例

3.3.4.1. AddVertex方法测试

向FriendshipGraph中添加点，然后判断这些点是否在图中，然后是重名测试，向图中添加具有相同name的另一个点。

3.3.4.2. AddEdge方法测试

测试单向边，确保只能从a到达b；测试双向边，添加从b到a的边，此时两个方向都应该连通。

@Test
public void addEdgeTest() {Person a = new Person("A");Person b = new Person("B");FriendshipGraph graph = new FriendshipGraph();graph.addVertex(a);graph.addVertex(b);//添加单向边graph.addEdge(a, b);assertTrue(a.getFriend().contains(b));assertFalse(b.getFriend().contains(a));//添加双向边graph.addEdge(b, a);assertTrue(b.getFriend().contains(a));
}

3.3.4.3. GetDistance方法测试

使用四个方法测试：

getDistance1：测试到达自身时返回距离为0；

getDiatance2：测试a与b不连通时返回的距离为-1；

getDistance3：测试单向到达时，从a到b返回的是ab之间的距离，而从b到a时返回的是-1；

/*** 单向到达：a-->b<-->c*/assertEquals(1, graph.getDistance(a, b));assertEquals(-1, graph.getDistance(b, a));assertEquals(2, graph.getDistance(a, c));assertEquals(-1, graph.getDistance(c, a));

getDistance4：测试在一个复杂的图中能够正确的返回两个点之间的最短距离。

/*** 多条路径* 	    b*   / /  \* 	/ /    \* a--e--f--c*  \ \   /*   \ \ / *     d*/assertEquals(2, graph.getDistance(a, c));

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！