P1044 [NOIP2003 普及组] 栈

P1044 [NOIP2003 普及组] 栈

题目背景
栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。
栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述
宁宁考虑的是这样一个问题：一个操作数序列，1,2… ,n,1,2,…,n（图示为 1 到 3 的情况），栈 A 的深度大于 n。
现在可以进行两种操作，
将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）
使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

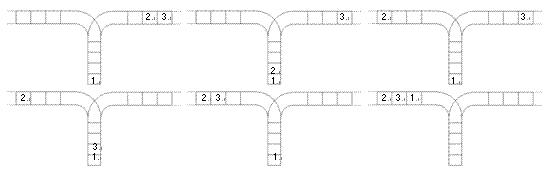
（原始状态如上图所示）
你的程序将对给定的 n，计算并输出由操作数序列 1,2,…,n，1,2,…,n 经过操作可能得到的输出序列的总数。

输入格式
输入文件只含一个整数 n(1≤n≤18）
输出格式
输出文件只有一行，即可能输出序列的总数目。
输入输出样例
输入
3
输出
5
说明/提示
【题目来源】
NOIP 2003 普及组第三题

对于这个题目，可以利用递归+记忆化搜索，递归用来推答案，记忆化用了省时间，当然还有卡特兰数这个方法来直接的得出答案。
方法一：设置一个二维数组f[i][j]，i表示在头端还有i个待排的数，j表示栈中有j个数，f[i][j]表示当前情况下输出序列的总数目。
如果此时你已经知道f[i][j]的数，那就返回即可。
1.如果头端为0个数，栈中有j个数，即f[0][j],那此时，因为栈的先进后出的特点，只有一种情况，即f[0][j]=1
2.如果此时栈为空，也就是f[i][0]的情况，能做的唯一操作就是把头部元素放进栈中，所以f[i[[0]=f[i-1][j+1]。
3.如果此时头部和栈中都不为0，那有两种操作，一是把栈中元素pop出，也就是f[i][j-1]。二是把头部元素放进栈中，也就是f[i-1][j+1]。所以此时f[i][j]=f[i-1][j+1]+f[i][j-1]。
至此，秉持着不重不漏从易到难的原则把所有情况都讨论完了。
下面附上代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int f[20][20];
int dfs(int i, int j)  // i是头部中里的数，j是栈中的数
{if (f[i][j]) return f[i][j];if (i == 0) return f[i][j] = 1;if(j==0) return f[i][j]=dfs(i-1,j+1);return f[i][j]=dfs(i-1,j+1)+dfs(i,j-1);
}
int main() {int n;cin >> n;cout << dfs(n, 0) << endl;return 0;
}

方法二：也就是直接套用卡特兰数的公式
设h(n)为catalan数的第n项，令h(0)=1,h(1)=1，catalan数满足递推式
$$h(n)=h(0)\ast h(n-1)+h(1)\ast h(n-2)+...+h(n-1)\ast h(0)(n\ge 2)$$
或
$$h[n]=h[n-1]\ast (4\ast n-2)/(n+1)$$
下面附上代码

#include<bits/stdc++.h>
using namespace std;
int h[20];
int main()
{int n;h[0]=h[1]=1;cin>>n;for(int i=2;i<=n;i++){for(int j=0;j<i;j++){h[i]+=h[j]*h[i-j-1];}}cout<<h[n]<<endl;
}

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll h[21];
int main()
{int n;h[0]=h[1]=1;cin>>n;for(int i=2;i<=n;i++){h[i]+=h[i-1]*(4*i-2)/(i+1);}cout<<h[n];return 0;
}

上述想法也是经过别人的指点，经过修改，才整理出来的。
如果你有任何建议或者批评和补充，请留言指出，不胜感激。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！