文章目录

• SmoothL1->IoU->GIoU->DIoU->CIoU Loss
• • SmoothL1
  • IoU LOSS
  • GIoU LOSS
  • Distance-IoU Loss(DIOU)
  • Complete-IoU(CIOU)

SmoothL1->IoU->GIoU->DIoU->CIoU Loss

SmoothL1

由微软rgb大神在Fast RCNN论文提出
设x为 真实值与预测值之间的差

• $L1\_LOSS=|x|$
  缺点：
  1） $L1\_LOSS$损失函数在0处不可导；
  2） $L1\_LOSS$对x的导数为常数，在训练后期，x很小时，如果learning rate 不变，损失函数会在稳定值附近波动，很难收敛到更高的精度。

• L 2 _ L O S S = ∣ x ∣ 2 L2\_LOSS = |x|^2 L2_LOSS=∣x∣2
  缺点：
  $L2\_LOSS$ 损失函数对x>1时的导数，其导数也非常大，给予二次方倍的惩罚，对离群点比较敏感，受其影响较大，可能梯度爆炸。

• Smooth L 1 ( x ) = { 0.5 x 2 i f ∣ x ∣ < 1 ∣ x ∣ − 0.5 o t h e r w i s e \text{Smooth}{L_1}(x) =\left \{ \begin{array}{c} 0.5x^2 & if \mid x \mid <1 \\ \mid x \mid - 0.5 & otherwise \end{array} \right. SmoothL1​(x)={0.5x2∣x∣−0.5​if∣x∣<1otherwise​
  综合二者的有点，规避二者的缺点，完美。

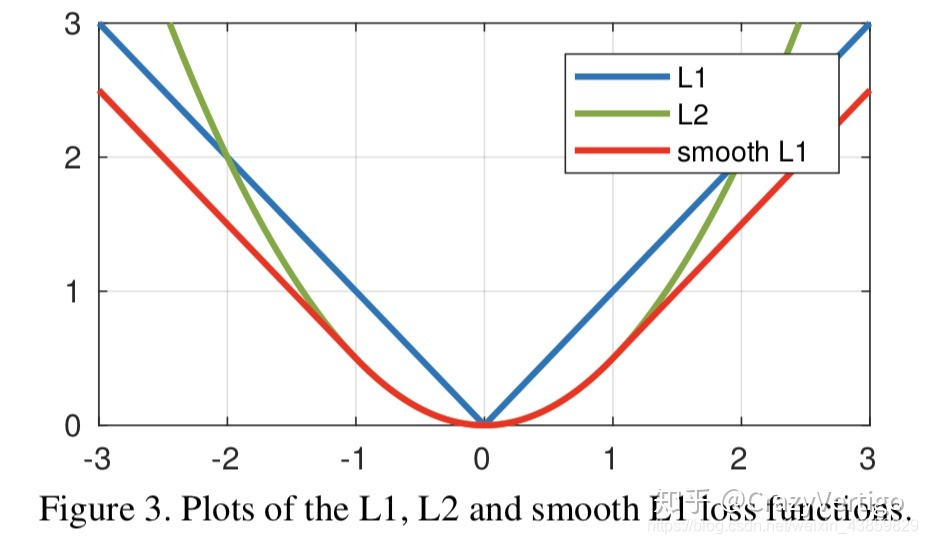
三种方式的缺点：
上面的三种Loss用于计算目标检测的Bounding Box Loss时，独立的求出4个点的Loss，然后进行相加得到最终的Bounding Box Loss，这种做法的假设是4个点是相互独立的，实际是有一定相关性的。实际评价框检测的指标是使用IOU，这两者是不等价的，多个检测框可能有相同大小的 S m o o t h L 1 ( x ) Smooth_{L_1}(x) SmoothL1​​(x) LOSS，但IOU可能差异很大，为了解决这个问题就引入了IOU LOSS。

IoU LOSS

由旷视提出，发表于2016 ACM。也可在我博客中找到具体的解读。

缺点：
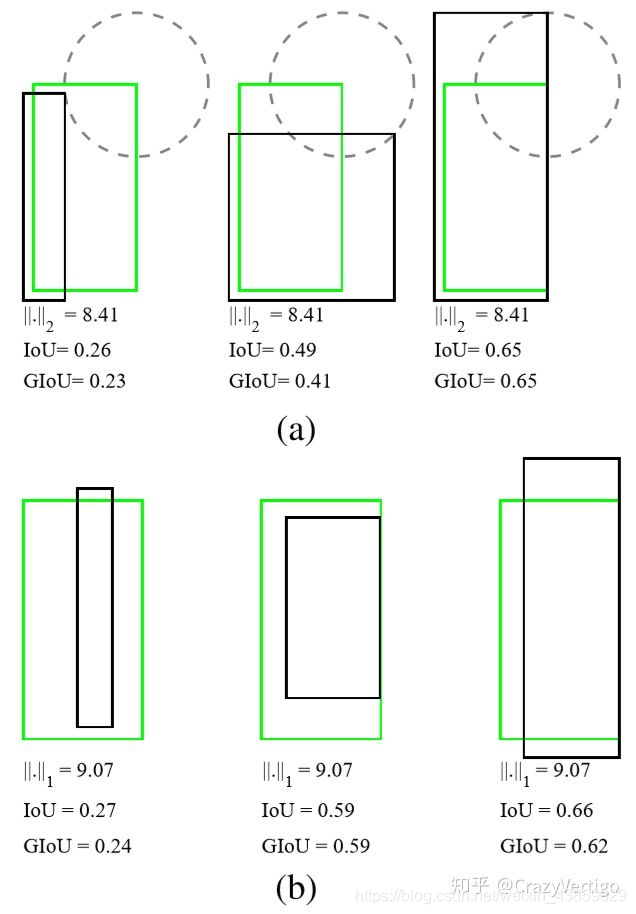
1）当预测框和目标框不相交时，IoU(A,B)=0时，不能反映A,B距离的远近，此时损失函数不可导，IoU Loss 无法优化两个框不相交的情况。
2）假设预测框和目标框的大小都确定，只要两个框的相交值是确定的，其IoU值是相同时，IoU值不能反映两个框是如何相交的。
如：
于是GIOU LOSS 被提出。

GIoU LOSS

由斯坦福学者提出，发表于CVPR2019

缺点：

当目标框完全包裹预测框的时候，IoU和GIoU的值都一样，此时GIoU退化为IoU, 无法区分其相对位置关系；此时作者提出的DIoU， 加入了中心点归一化距离，所以可以更好地优化此类问题。

位置暴露了缺点，于是DIOU LOSS 被提出。

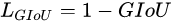
Distance-IoU Loss(DIOU)

Distance-IoU Loss 论文地址

D I O U = I O U − ( d / c ) 2 DIOU=IOU-(d/c)^2 DIOU=IOU−(d/c)2

上述损失函数中，b，bgt分别代表了anchor框和目标框的中心点，且p代表的是计算两个中心点间的欧式距离。c代表的是能够同时覆盖anchor和目标框的最小矩形的对角线距离。因此DIoU中对anchor框和目标框之间的归一化距离进行了建模。直观的展示如下图所示。

特点及缺点：
1） 尺度不变性；
2）当两个框完全重合时DIOU=0；
3）当2个框不相交时，仍然可以为边界框计算损失，并提供移动方向。
4）DIoU Loss可以直接优化2个框直接的距离，比GIoU Loss收敛速度更快
5）对于目标框包裹预测框的这种情况，DIoU Loss可以收敛的很快，而GIoU Loss此时退化为IoU Loss收敛速度较慢；

Complete-IoU(CIOU)

C I O U = I O U − ( d / c ) 2 − a v CIOU=IOU-(d/c)^2-av CIOU=IOU−(d/c)2−av
论文考虑到bbox回归三要素中的长宽比还没被考虑到计算中，因此，进一步在DIoU的基础上提出了CIoU。其惩罚项如下面公式：

CIoU的惩罚项是在DIoU的惩罚项基础上加了一个影响因子av,

a 为权重

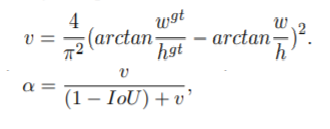
experiment:

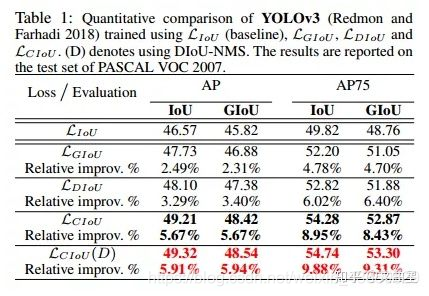
【完结】

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！