概念

1. 路径：树中一个结点到另一个结点之间的分支序列构成两个结点间的路径
2. 路径长度：路径上的分支数目
3. 树的路径长度：树根到每个结点的路径长度的和
4. 结点带权路径长度：结点到树根的路径长度与结点的权的乘积
5. 树的带权路径长度：树的带权路径长度为树中所有叶子节点的带权路径长度之和，通常记作WPL=∑WkLk。
6. 假设有n个权值{w1,w1,…wn}，试构造一棵有n个叶子节点的二叉树，每个叶子节点带权为wi，则其中带权路径长度WPL最小的二叉树称作最优二叉树或霍夫曼树。
7. 前缀编码：设计长短不等的编码，必须是任一字符的编码都不是另一个字符编码的前缀，这种编码称为前缀编码.

霍夫曼树构造步骤

1. 根据给定的n个权值(W1,W2,W3….)构造n棵二叉树的集合F={T1，T2，T3…}其中每棵二叉树Ti只有一个带权为Wi的根结点，其左右子树为空。
2. 在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和。
3. 在F中删除选中的这两个树，同时将新得到的二叉树加入F中。
4. 重复(2)(3)操作，直到F只含一棵树为止。这棵树便是霍夫曼树。

霍夫曼编码

我们都知道，计算机是基于电信号通断的二进制数据流信息传输，比如我们要传输一串字符“ABCDEBCDBB”，我们就要用01组合来表示所有的字符，显然该字符串里有5种字符，2^2 < 5< 2^3，所以我们需要至少三位二进制表示所有的字符这样一来表示这串十个字符的信息就要使用10 * 3 = 30个数，再看这串字符，不难发现B，C，D的使用频率很高，那么如果我们提供一种方法使表示信息中常用字符的编码减少，那么整体的编码长度肯定会大大减少。比如如果我们可以用2位来表示B，C，D，即使这样的代价是使用4位编码来区分余下的A，E，那么总编码长度为 2 * 4+8 *2 = 24，相对于30个数的编码有了显著的减少，对于十个字符的信息都能有着显著的成效，那么实际中成千上万的信息肯定会大大减少编码量。

霍夫曼编码就是基于这种思想应运而生，上文中介绍的霍夫曼树节点的权重，就是实际编码中每个字符的出现频率。霍夫曼编码就是根据字符出现频率（次数），映射为叶子节点权重，建立霍夫曼树，设立0/1路径，得到前缀编码的过程。

霍夫曼解码过程

解码过程就是编码过程的逆过程，对于确定的一串霍夫曼编码，从根节点开始沿着编码中的二进制顺序找到叶子节点获取字符，应用前缀编码的特性，解码出一个字符又重新开始从根节点进行下一次解码。

构造示例

4 个叶子结点 a、b、c、d，分别带权7、5、2、4。构造流程画图说明一下：

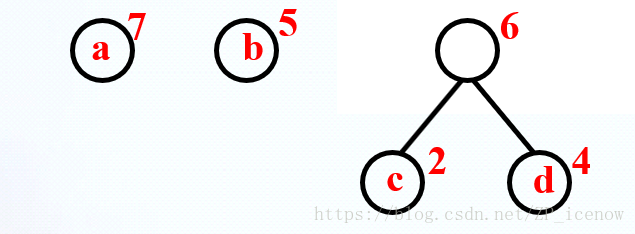
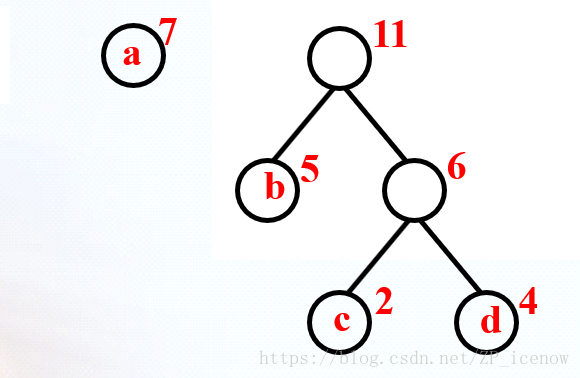
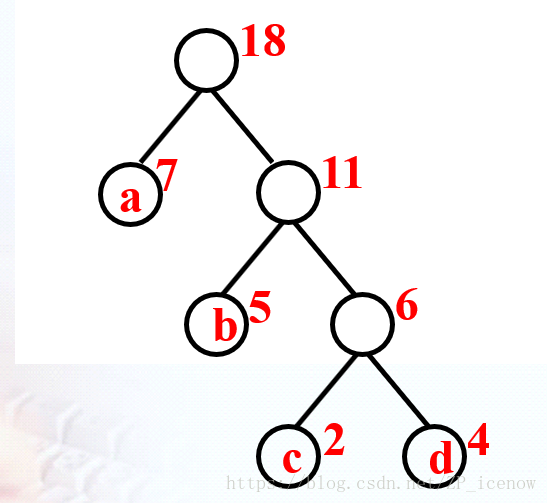
代码实现

代码：

class HuffmanNode
{public $data = '';public $weight = 0;public $parent = null;public $left = null;public $right = null;public function __construct($data='', $weight=0, $left=null, $right=null){$this->data = $data;$this->weight = $weight;$this->left = $left;$this->right = $right;}
}class HuffmanTree
{private $wpl = 0;private $root = null; // private $nodes = []; // 保存各个叶子节点的数据public function create($nodes){// 重复(2)(3)操作，直到F只含一棵树为止。while (count($nodes) > 1) {// 按由小到大排序usort($nodes, function($a, $b){return ($a->weight > $b->weight) ? 1 : -1;});// 在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，// 且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和。$parent_node = new HuffmanNode('', ($nodes[0]->weight + $nodes[1]->weight), $nodes[0], $nodes[1]);$nodes[0]->parent = $parent_node;$nodes[1]->parent = $parent_node;// 在F中删除选中的这两个树，同时将新得到的二叉树加入F中。array_shift($nodes);array_shift($nodes);$nodes[] = $parent_node;}$this->root = $nodes[0];}private function printNodes($node, $depth=0){if(!empty($node)){$this->printNodes($node->left, $depth+1);for ($i=0; $i < $depth; $i++) { echo '--';}$data = empty($node->data) ? '_': $node->data;$weight = $node->weight;echo "{$weight}:{$data}\n";$this->printNodes($node->right, $depth+1);}}public function print(){$this->printNodes($this->root);}private function coding($node, $depth=0, $code = []){if(!empty($node)){$code[] = '0';$this->coding($node->left, $depth+1, $code);// 从左子树上弹出多压入的编码array_pop($code);// 说明是叶子节点，开始保存数据if(empty($node->left) && empty($node->right)) {$this->nodes[$node->data] = ['weight' => $node->weight,'path_length' => $depth,'code' => implode('', $code),];}$code[] = '1';$this->coding($node->right, $depth+1, $code);}}public function huffmanCodes(){$this->coding($this->root);return $this->nodes;}
}$HuffmanTree = new HuffmanTree();$nodes = [];
$nodes[] = new HuffmanNode('A', 5);
$nodes[] = new HuffmanNode('B', 29);
$nodes[] = new HuffmanNode('C', 7);
$nodes[] = new HuffmanNode('D', 8);
$nodes[] = new HuffmanNode('E', 14);
$nodes[] = new HuffmanNode('F', 23);
$nodes[] = new HuffmanNode('G', 3);
$nodes[] = new HuffmanNode('H', 11);$HuffmanTree->create($nodes);echo '打印霍夫曼树：', PHP_EOL;
$HuffmanTree->print();$huffman_codes = $HuffmanTree->huffmanCodes();echo '霍夫曼编码信息：', PHP_EOL;
print_r($huffman_codes);

输出：

打印霍夫曼树：
--------3:G
------8:_
--------5:A
----19:_
------11:H
--42:_
----23:F
100:_
----29:B
--58:_
------14:E
----29:_
--------7:C
------15:_
--------8:D
霍夫曼编码信息：
Array
([G] => Array([weight] => 3[path_length] => 4[code] => 0000)[A] => Array([weight] => 5[path_length] => 4[code] => 0001)[H] => Array([weight] => 11[path_length] => 3[code] => 001)[F] => Array([weight] => 23[path_length] => 2[code] => 01)[B] => Array([weight] => 29[path_length] => 2[code] => 10)[E] => Array([weight] => 14[path_length] => 3[code] => 110)[C] => Array([weight] => 7[path_length] => 4[code] => 1110)[D] => Array([weight] => 8[path_length] => 4[code] => 1111))

【参考】

1. https://blog.csdn.net/ZP_icenow/article/details/81041215

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！