【java算法】赫夫曼树(Huffman)的构建和应用(编码、译码)
赫夫曼树的概念
要了解赫夫曼树,我们要首先从扩充二叉树说起
二叉树结点的度
结点的度指的是二叉树结点的分支数目, 如果某个结点没有孩子结点,即没有分支,那么它的度是0;如果有一个孩子结点, 那么它的度数是1;如果既有左孩子也有右孩子, 那么这个结点的度是2.
扩充二叉树
对于一颗已有的二叉树, 如果我们为它添加一系列新结点, 使得它原有的所有结点的度都为2,那么我们就得到了一颗扩充二叉树, 如下图所示:
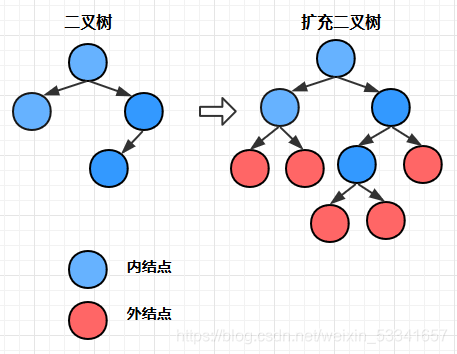
其中原有的结点叫做内结点(非叶子结点), 新增的结点叫做外结点(叶子结点)
我们可以得出: 外结点数 = 内结点数 + 1
并进一步得出: 总结点数 = 2 × 外结点数 -1
扩充二叉树,构成了赫夫曼树的基本形态,而上面的公式,也是我们构建赫夫曼树的依据之一
赫夫曼树的外结点和内结点
赫夫曼树的外结点和内结点的性质区别:外节点是携带了关键数据的结点, 而内部结点没有携带这种数据, 只作为导向最终的外结点所走的路径而使用
正因如此,我们的关注点最后是落在赫夫曼树的外结点上, 而不是内结点。
带权路径长度WPL
让我们思考一下: 在一颗在外结点上存储了数据的扩充二叉树中进行查找时,数据结点怎么分布才能尽可能减少查找的开销呢? 这里我们再加上一个前提:不同的数据结点搜索的频率(或概率)是不一致的。
显然, 我们大致的思路是: 如果一个数据结点搜索频率越高,就让它分布在离根结点越近的地方,也即从根结点走到该结点经过的路径长度越短。 这样就能从整体上优化整颗树的性能。
频率是个细化的量,这里我们用一个更加标准的一个词描述它——“权值”。
综上, 我们为扩充二叉树的外结点(叶子结点)定义两条属性: 权值(w)和路径长度(l)。同时规定带权路径长度(WPL)为扩充二叉树的外结点的权值和路径长度乘积之和:
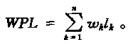
(注意只是外结点!)
赫夫曼树(最优二叉树)
由n个权值构造一颗有n个叶子结点的二叉树, 则其中带权路径长度WPL最小的二叉树, 就是赫夫曼树,或者叫做最优二叉树。
例如下图中对a, b, c
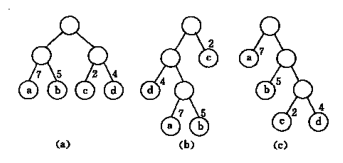
对a: WPL = 7×2 + 5×2 + 2×2 + 4×2 = 36;
对b: WPL = 7×3 + 5×3 + 2×1 + 4×2 = 46;
对c: WPL = 7×1 + 5×2 + 2×3 + 4×3 = 35;
c中WPL最小, 可以验证, 它就是赫夫曼树, 而a和b都不是赫夫曼树
对于同一组权值的叶结点, 构成的赫夫曼树可以有多种形态, 但是最小WPL值是唯一的。
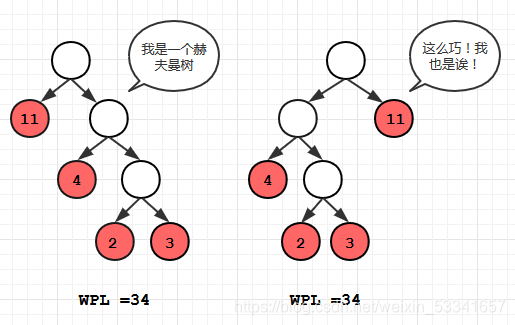
赫夫曼树的构建
构建过程分四步:
- 根据给定的n个权值{w1, w2, w3 … wn }构成n棵二叉树的集合, 每棵二叉树都只包含一个结点
- 在上面的二叉树中选出两颗根结点权值最小的树, 同时另外取一个新的结点作为这两颗树的根结点, 设新节点的权值为两颗权值最小的树的权值和, 将得到的这颗树也加入到树的集合中
- 在2操作后, 从集合中删除权值最小的那两颗树
- 重复2和3,直到集合中的树只剩下一棵为止, 剩下的这颗树就是我们要求得的赫夫曼树。
如下图所示:
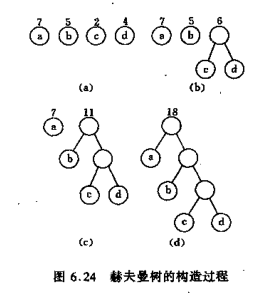
(注意a和b的分界线在4和7中间,图中画的不是很清晰)
我们上面提到过WPL相同的情况下, 赫夫曼树不止一种,在我们介绍的算法中,人为要求某个内结点的左儿子的权值要比右儿子大, 这样一来, 就将我们算法中的赫夫曼树变为唯一一种了。
构建赫夫曼树的的方法有多种,但基于实际应用的考虑(赫夫曼编码和译码), 下面我给出基于数组存储实现的赫夫曼树:
Node类的设计
我们首先需要一个编写一个结点类, 结点类里有5种实例变量: weight表示权值, data表示外结点存储的字符,data属性在下面的编码/解码中会用到。 而同样因为赫夫曼编码,解码的需求,这里我们使用三叉链实现二叉树,,即在left和right属性的基础上,为结点增加了parent属性,目的是能够从叶子结点上溯到根结点,从而实现赫夫曼编码。
/*** @Author: HuWan Peng* @Date Created in 23:21 2018/1/14*/
public class Node {char data; // 数据int weight; // 权值int left, right, parent; // 三条链接public Node (char data, int weight) {this.data = data;this.weight = weight;}//需要获取资料的朋友请加Q君样:290194256*public Node (int weight) {this.weight = weight;}
}
buildTree方法的设计
输入参数和返回值
输入参数: 一个由外结点对象组成的Node数组, 假设其为nodes
返回值: 一个由内、外结点共同组成,且建立了链接关系的Node数组, 假设其为HT(HuffmanTree)
具体操作
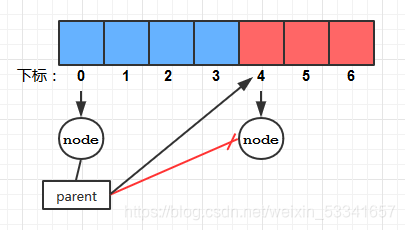
首先要做的事情是: 获取输入的nodes数组的长度 n , 创建一个长度为 2n - 1的数组——HT,在数组HT中, 前n个元素用来存放外结点, 后n个元素用来存放内结点, 如下图所示:
图A
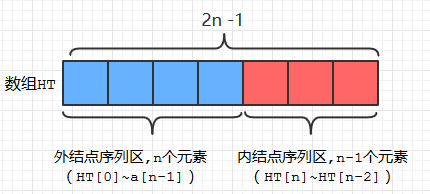
图B
接下来要做的是:
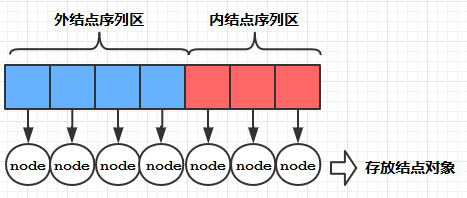
- 初始化HT中的结点对象,此时各个结点对象的weight都被置为0
- 将输入的nodes数组中的各结点对象的权值赋给HT[0]~ HT[n-1], 如上图所示
3.通过循环, 依次计算各个内结点的权值,同时建立该内结点和作为它左右孩子的两个外结点的链接关系。
易知:当最后一个内结点的权值也计算完毕后, 整颗赫夫曼树也就构建完毕了。
如图 (方框内数字表示结点对象的权值)
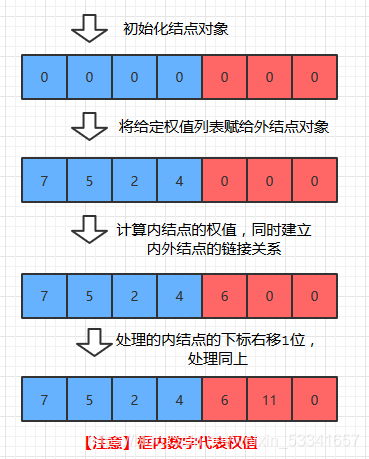
注意要点
要注意的是: 我们为Node设置的链接变量left/right/parent是整型的, 它指向的是某个结点对象在HT中的下标, 而不是结点对象本身! 这种实现方式和一般的树是有区别的
具体代码
下面是buildTre方法的代码:
(select方法尚未给出)
/*** @description: 构建赫夫曼树*/public Node[] buildTree (Node [] nodes) {int s1, s2,p;int n = nodes.length; // 外结点的数量int m = 2*n - 1; // 内结点 + 外结点的总数量Node [] HT = new Node [m]; // 存储结点对象的HT数组for (int i=0;ibuildTree方法的用例:
/*** @description: buildTree方法的用例*/public static void main (String [] args) {Node [] nodes = new Node[4];nodes[0] = new Node('a',7);nodes[1] = new Node('b',5);nodes[2] = new Node('c',2);nodes[3] = new Node('d',4);HuffmanTree ht = new HuffmanTree();Node [] n = ht.buildTree(nodes); // n是构建完毕的赫夫曼树}
}
elect方法的设计
buildTree方法的实现依赖于select方法:
private int select (Node[] HT,int range, int rank)
上面代码中调用select的部分为:
s1 = select(HT,i,0); // 取得HT数组中权值最小的结点对象的下标
s2 = select(HT,i,1); // 取得HT数组中权值次小的结点对象的下标
思考3个问题:
- 求给定权值排名的结点,可以先对数组进行从小到大的快速排序, 然后就可以取得给定排名的结点对象了, 但是如果直接对输入的HT数组进行排序的话, 会改变HT数组元素的排列顺序, 这将不利于我们下面要介绍的赫夫曼编码的方法的实现。 所以这里我们先将HT数组拷贝到一个辅助数组copyNodes中, 对copyNodes进行快排,并取得给定权值排名的结点对象。然后通过遍历HT数组,比较得到该结点对象在HT中的下标
- 在上面我们提到过, 在构建一颗新二叉树后, 要把原来的两颗权值最小的树从集合中 ”删除“,这里我们通过类内的selectStart实例变量实现, selectStart初始值为0, 每次构建一棵新二叉树后都通过 selectStart+=2; 增加它的值。(见上文buildTree代码) 这样, 在select方法中就可以通过copyNodes[selectStart + rank],去取得 “删除” 后权值排名为rank的结点对象了。
- 引入range这一参数是为了排除那些weight仍为0,即尚未使用到的内结点, 防止排序后取到它们。注意, 随着循环中 i 的增长, range也是不断增长的:
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!