强指定验证人签名方案可以使签名者说服指定验证人，使指定验证人无法将签名转让给第三方，甚至没有第三方可以验证指定验证人签名的有效性

Identity-based strong designated verifier signature schemes: Attacks and new construction

• 基于id的指定验证者签名
• • Zhang-Mao scheme
  • Lal-Verma scheme
  • 针对两个方案的攻击
• 新方案
• • 基于身份的指定验证者签名方案

基于id的指定验证者签名

Zhang-Mao scheme

Setup:
e : G 1 × G 1 → G 2 e:G_1\times G_1\rightarrow G_2 e:G1​×G1​→G2​, order $q$, 任意生成元$P$； H 1 : { 0 , 1 } ∗ → G 1 H_1:\{0,1\}^*\rightarrow G_1 H1​:{0,1}∗→G1​； H 2 : { 0 , 1 } ∗ × G 1 × G 1 → G 1 H_2:\{0,1\}^*\times G_1\times G_1\rightarrow G_1 H2​:{0,1}∗×G1​×G1​→G1​
msk: s ∈ Z q ∗ s\in Z_q^* s∈Zq∗​,mpk: P p u b = s P P_{pub}=sP Ppub​=sP

KeyExtract:
S I D = s H 1 ( I D ) , Q I D = H 1 ( I D ) S_{ID}=sH_1(ID),Q_{ID}=H_1(ID) SID​=sH1​(ID),QID​=H1​(ID)

Sgin ( Q I D A , Q I D B , M , r 1 , r 2 ∈ Z q ∗ ) → ( U 1 , U 2 , V ) (Q_{ID_A},Q_{ID_B},M,r_1,r_2\in Z_q^*)\rightarrow(U_1,U_2,V) (QIDA​​,QIDB​​,M,r1​,r2​∈Zq∗​)→(U1​,U2​,V)给指定验证方 I D B ID_B IDB​

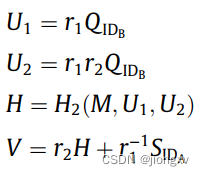
Verify ( ( U 1 , U 2 , V ) , M ) ((U_1,U_2,V),M) ((U1​,U2​,V),M)
H = H 2 ( M , U 1 , U 2 ) H=H_2(M,U_1,U_2) H=H2​(M,U1​,U2​)
验证
e ( U 1 , V ) = e ( U 2 , H ) e ( S I D B , Q I D A ) e(U_1,V)=e(U_2,H)e(S_{ID_B},Q_{ID_A}) e(U1​,V)=e(U2​,H)e(SIDB​​,QIDA​​)

============
e ( U 1 , V ) = e ( r 1 Q I D B , r 2 H ) e ( r 1 Q I D B , r 1 − 1 S I D A ) = e ( U 2 , H ) e ( S I D B , Q I D A ) e(U_1,V)=e(r_1Q_{ID_B},r_2H)e(r_1Q_{ID_B},r_1^{-1}S_{ID_A})=e(U_2,H)e(S_{ID_B},Q_{ID_A}) e(U1​,V)=e(r1​QIDB​​,r2​H)e(r1​QIDB​​,r1−1​SIDA​​)=e(U2​,H)e(SIDB​​,QIDA​​)

============
Transcript simulation:
指定的验证者Bob随机选择两个数字 r 1 ′ , r 2 ′ r_1',r_2' r1′​,r2′​并计算

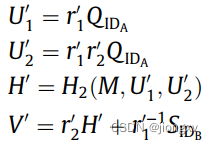
生成的 ( U 1 ′ , U 2 ′ , V ′ ) (U_1',U_2',V') (U1′​,U2′​,V′)也满足验证

Lal-Verma scheme

Setup和Key generation与Zhang-Mao 相同，除了 H 2 : { 0 , 1 } ∗ × G 2 → G 1 H_2:\{0,1\}^*\times G_2\rightarrow G_1 H2​:{0,1}∗×G2​→G1​
Proxy key generation:
原签名方Alice生成签名：

• random r 1 , r 2 , r 3 ∈ Z q ∗ r_1,r_2,r_3\in Z_q^* r1​,r2​,r3​∈Zq∗​，授权凭证$W$
• U 1 = r 1 Q I D B , U 2 = r 2 Q I D A , U 3 = r 3 U 1 U_1=r_1Q_{ID_B},U_2=r_2Q_{ID_A},U_3=r_3U_1 U1​=r1​QIDB​​,U2​=r2​QIDA​​,U3​=r3​U1​
• V = r 3 H + r 1 − 1 S I D A , H = H 2 ( M , W , e ( r 2 Q I D B , S I D A ) ) V=r_3H+r_1^{-1}S_{ID_A},H=H_2(M,W,e(r_2Q_{ID_B},S_{ID_A})) V=r3​H+r1−1​SIDA​​,H=H2​(M,W,e(r2​QIDB​​,SIDA​​))
• σ = ( M , W , U 1 , U 2 , U 3 , V ) \sigma=(M,W,U_1,U_2,U_3,V) σ=(M,W,U1​,U2​,U3​,V)发给代理签名方Bob
  代理方Bob:
• H = H 2 ( M , W , e ( U 2 , S I D B ) ) H=H_2(M,W,e(U_2,S_{ID_B})) H=H2​(M,W,e(U2​,SIDB​​)).
• 查验 e ( U 1 , V ) = e ( U 3 , H ) e ( S I D B , Q I D A ) e(U_1,V)=e(U_3,H)e(S_{ID_B},Q_{ID_A}) e(U1​,V)=e(U3​,H)e(SIDB​​,QIDA​​)
• 计算proxy secret key S I D P = V + S I D B S_{IDP}=V+S_{ID_B} SIDP​=V+SIDB​​

Proxy signature generation:
Bob:

• random t 1 , t 2 , t 3 ∈ Z q ∗ t_1,t_2,t_3\in Z_q^* t1​,t2​,t3​∈Zq∗​
• X 1 = t 1 Q I D C , X 2 = t 2 S I D P , X 3 = t 3 X 1 X_1=t_1Q_{ID_C},X_2=t_2S_{IDP},X_3=t_3X_1 X1​=t1​QIDC​​,X2​=t2​SIDP​,X3​=t3​X1​
• X = t 3 H 1 + t 1 − 1 S I D P , H 1 = H 2 ( M , W , e ( t 2 Q I D C , S I D P ) ) X=t_3H^1+t_1^{-1}S_{IDP},H^1=H_2(M,W,e(t_2Q_{ID_C},S_{IDP})) X=t3​H1+t1−1​SIDP​,H1=H2​(M,W,e(t2​QIDC​​,SIDP​))
• 代理签名 ( M , W , X 1 , X 2 , X 3 , X , V ) (M,W,X_1,X_2,X_3,X,V) (M,W,X1​,X2​,X3​,X,V)发给指定接收方Cindy

Proxy signature verification:
Cindy:

• 检查消息$M$是否确认到授权$W$
• 检查是否分别将Alice和Bob指定为授权$W$中的原始签名者和代理签名者
• 计算 H 1 = H 2 ( M , W , e ( X 2 , Q I D C ) ) H^1=H_2(M,W,e(X_2,Q_{ID_C})) H1=H2​(M,W,e(X2​,QIDC​​))
• 查验 e ( X 1 , X ) = e ( X 3 , H 1 ) e ( S I D C , Q I D B ) e ( Q I D C , V ) e(X_1,X)=e(X_3,H^1)e(S_{ID_C},Q_{ID_B})e(Q_{ID_C},V) e(X1​,X)=e(X3​,H1)e(SIDC​​,QIDB​​)e(QIDC​​,V)

针对两个方案的攻击

Zhang-Mao scheme：声称他们的方案是一个强指定验证者签名，甚至没有第三方可以验证指定验证者签名的有效性，因为在验证方程中需要指定验证者的私钥。这几个性质实际上并不满足

• 假设 ( U 1 , U 2 , V ) (U_1,U_2,V) (U1​,U2​,V)是消息$M$的签名，任何拦截了 ( U 1 , U 2 , V ) (U_1,U_2,V) (U1​,U2​,V)签名的人可以根据验证方程计算 e ( S I D B , Q I D A ) e(S_{ID_B},Q_{ID_A}) e(SIDB​​,QIDA​​)： e ( U 1 , V ) = e ( U 2 , H ) e ( S I D B , Q I D A ) e(U_1,V)=e(U_2,H)e(S_{ID_B},Q_{ID_A}) e(U1​,V)=e(U2​,H)e(SIDB​​,QIDA​​)
• 在这之后，如果攻击者又拦截了消息 M ∗ M^* M∗的签名 ( U 1 ∗ , U 2 ∗ , V ∗ ) (U_1^*,U_2^*,V^*) (U1∗​,U2∗​,V∗)，可以通过 e ( U 1 ∗ , V ∗ ) = e ( U 2 ∗ , H ∗ ) e ( S I D B , Q I D A ) e(U_1^*,V^*)=e(U_2^*,H^*)e(S_{ID_B},Q_{ID_A}) e(U1∗​,V∗)=e(U2∗​,H∗)e(SIDB​​,QIDA​​)验证签名。即攻击者无需指定验证者的私钥就能验证签名

Lal-Verma scheme：类似地，攻击者也可以很容易地拦截获取 e ( S I D C , Q I D B ) e(S_{ID_C},Q_{ID_B}) e(SIDC​​,QIDB​​)根据验证方程： e ( X 1 , X ) = e ( X 3 , H 1 ) e ( S I D C , Q I D B ) e ( Q I D C , V ) e(X_1,X)=e(X_3,H^1)e(S_{ID_C},Q_{ID_B})e(Q_{ID_C},V) e(X1​,X)=e(X3​,H1)e(SIDC​​,QIDB​​)e(QIDC​​,V)，当再次拦截到签名，也可以直接验证 e ( X 1 ∗ , X ∗ ) = e ( X 3 ∗ , H 1 ∗ ) e ( S I D C , Q I D B ) e ( Q I D C , V ∗ ) e(X_1^*,X^*)=e(X_3^*,H^{1*})e(S_{ID_C},Q_{ID_B})e(Q_{ID_C},V^*) e(X1∗​,X∗)=e(X3∗​,H1∗)e(SIDC​​,QIDB​​)e(QIDC​​,V∗)

新方案

基于身份的指定验证者签名方案

Setup和Key generation与Zhang-Mao 相同，除了 H 2 : { 0 , 1 } ∗ × G 2 → G 1 H_2:\{0,1\}^*\times G_2\rightarrow G_1 H2​:{0,1}∗×G2​→G1​（和Lal-Verma相同）
Sign ( M , Q I D A , Q I D C ) → ( U , σ ) (M,Q_{ID_A},Q_{ID_C})\rightarrow(U,\sigma) (M,QIDA​​,QIDC​​)→(U,σ)

• random r ∈ Z q ∗ r\in Z_q^* r∈Zq∗​
• U = r Q I D A U=rQ_{ID_A} U=rQIDA​​
• σ = H 2 ( M , e ( r Q I D C , S I D A ) ) \sigma=H_2(M,e(rQ_{ID_C},S_{ID_A})) σ=H2​(M,e(rQIDC​​,SIDA​​))发给Cindy

Verify
查验： σ = H 2 ( M , e ( U , S I D C ) ) \sigma=H_2(M,e(U,S_{ID_C})) σ=H2​(M,e(U,SIDC​​))
Signature simulation:
Cindy选择随机数 r ′ ∈ Z q ∗ r'\in Z_q^* r′∈Zq∗​并计算：

• U ′ = r ′ Q I D A U'=r'Q_{ID_A} U′=r′QIDA​​
• σ ′ = H 2 ( M , e ( U ′ , S I D C ) ) \sigma'=H_2(M,e(U',S_{ID_C})) σ′=H2​(M,e(U′,SIDC​​))
  生成的签名也是可验证的。

这个签名结构简单所以后面就不赘述了…仅作为对指定验证者签名的初步了解

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！