[回溯法]77.组合（回溯+剪枝）78.子集 90.子集II （解集去重）79.单词搜索（二维平面回溯）

• 77.组合（回溯+剪枝）
• • 思路1：回溯法
  • • 实现代码（剪枝前）：
    • 剪枝：（难点）
    • 实现代码（剪枝后）：
• 78.子集（不含重复元素的解集去重）
• • 题目分析
  • 思路：回溯法
  • • 关键问题
    • • 1、避免解集出现重复
      • 2、特殊解的处理
    • 实现代码
• 90.子集 II（含重复元素的解集去重）
• • 题目分析：
  • 思路：回溯法
  • • 解集重复问题
    • • 1、进入下一层递归带来的重复解
      • 2、for循环带来的重复解问题
    • 心得：（重要！）
    • 实现代码
• 79.单词搜索（二维平面上回溯）
• • 题目分析
  • 思路：回溯法
  • • 关键问题：
    • • 1、如何选择一个点的上下左右相邻节点？
      • 2、选择相邻节点时要考虑哪些问题？
    • 实现遇到的问题:
    • • 问题1：对上下左右邻接点的选取代码有错
      • 问题2：没有检验word的最后一个字符
    • 实现代码

之前整理过一部分回溯法的题型，见：[回溯法整理] 46.47.全排列I II 50.N皇后。
本文是对这部分的补充。

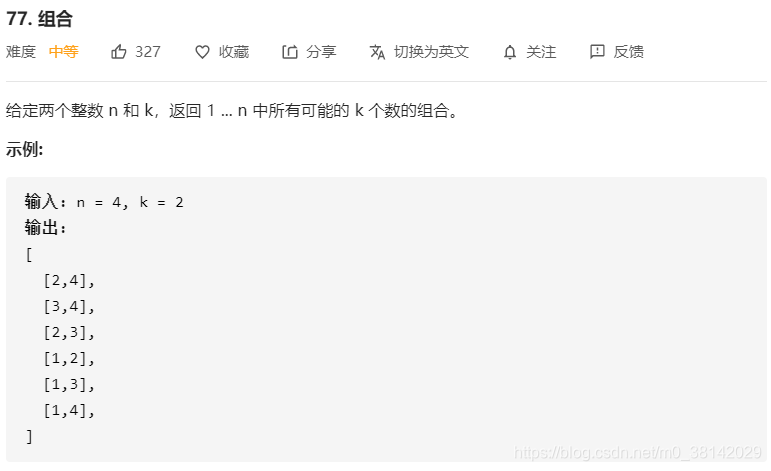
77.组合（回溯+剪枝）

题目链接：77.组合

分类：回溯法、剪枝处理

思路1：回溯法

• 状态变量：used数组标记1~n的数字是否被使用过，depth表示递归深度，等于生成的组合大小，这里当depth==k时就说明得到一个k个数的组合。
• 存储变量：List res存放最终的解集，List list存放一个解，在depth==k时将list加入到res中。
  注意[123]和[132]是同一个组合，所以对于每一层递归，可选的数字都是在前几轮剩下的数字里选择的，所以for-i循环的起点cur要等于上一轮所选的数字的下一个数字，所以进入下一层递归的函数参数设置如下：

函数定义：backtrack(int n, int k, int depth, int cur, List<Integer> list);//cur就是for-i循环的起点进入下一层递归（注意参数传递）：backtrack(n, k, depth + 1, i + 1, list);

实现代码（剪枝前）：

class Solution {List<List<Integer>> res;public List<List<Integer>> combine(int n, int k) {this.res = new ArrayList<>();//特殊用例if(k > n || k < 1 || n < 1) return res;List<Integer> list = new ArrayList<>();backtrack(n, k, 0, 1, list);return res;}//回溯的递归实现public void backtrack(int n, int k, int depth, int cur, List<Integer> list){if(depth == k){res.add(new ArrayList<>(list));}else{//剪枝前for(int i = cur; i <= n; i++){list.add(i);backtrack(n, k, depth + 1, i + 1, list);list.remove(list.size() - 1);}}}
}

剪枝：（难点）

例如：n = 6, k = 3时，
假设程序运行到list=[156]，接下来要移出6，同时因为第三个数字6已经到达for循环的末尾n，没有剩余数字可选，所以返回上一层的状态[15]，现在要取5之后的数字替换掉第二个数字，可以发现此时可供选择的数字只剩下6，但6替换5之后的状态为[16]，这样第三个数字就不存在可选数字了，所以在第二层递归的for循环中，i=6是可以直接跳过的。

同理假设程序运行到list=[456]，接下来移出6，基于上面的分析第二个数字取6之后第三个数字就没有剩余数字可用，所以也移出5，此时状态为[4]，第1个数字选择下一个5替换掉4，得到状态[5]，可以发现如果继续取[56]，则第三个数字又没有数字可用，所以第一个数字在i>=5都可以跳过。

整理可以发现for-i循环的上界条件和i,n,depth有关（depth值==当前组合里数字的个数，例如：在[]选择第一个数字时，depth=0，[1]时depth=1）：

n - i + 1:剩余的可选数字个数，k-depth：构成k个数的组合所欠缺的数字个数
剩余的可选数字个数要 >= 构成组合所欠缺的数字个数，
所以：
n - i + 1 >= k - depth
整理得：
i <= n - k + depth + 1

所以for循环修改为：

for(int i = cur; i <= n - k + depth + 1; i++)

实现代码（剪枝后）：

class Solution {List<List<Integer>> res;public List<List<Integer>> combine(int n, int k) {this.res = new ArrayList<>();//特殊用例if(k > n || k < 1 || n < 1) return res;List<Integer> list = new ArrayList<>();backtrack(n, k, 0, 1, list);return res;}//回溯的递归实现public void backtrack(int n, int k, int depth, int cur, List<Integer> list){if(depth == k){res.add(new ArrayList<>(list));}else{//增加了剪枝条件for(int i = cur; i <= n - k + depth + 1; i++){list.add(i);backtrack(n, k, depth + 1, i + 1, list);list.remove(list.size() - 1);}}}
}

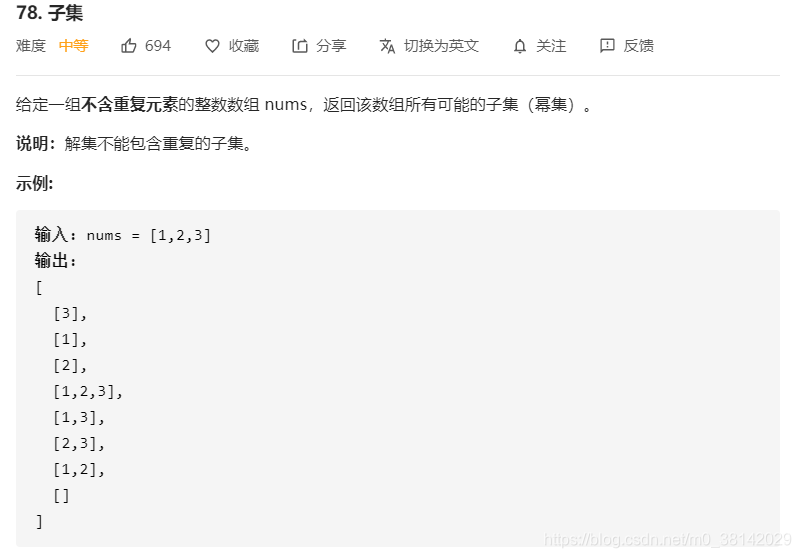
78.子集（不含重复元素的解集去重）

题目链接：78.子集

分类：回溯法

题目分析

很基础的回溯题，和求全排列的回溯解法类似，不同点在于全排列是要构造出一个完整的全排列后才加入解集中，而本题每向list加入一个元素，就构成一个解，将当前list作为一个解加入解集res中。

本题锻炼的是递归函数参数的传递，和 for循环起点终点的设置。基础都是回溯法整理-1中提到的“对for循环和进入下一层递归”的实际意义的理解。

思路：回溯法

关键问题

1、避免解集出现重复

重复问题例如：[1,2]和[2,1]认为是同一个解集，
解决方法：每一层递归的for循环都从上一层递归所选的数字的下一个开始选起。关键点在于for循环起点的设置和递归函数的参数传递

2、特殊解的处理

其中[]也认为是一个解。
当nums=[]时，[]就是一个解。
所以在最开始时要先将[]加入最终的解集：

List<Integer> list = new ArrayList<>();
res.add(new ArrayList<>(list));//加入特殊解[]

实现代码

class Solution {List<List<Integer>> res;public List<List<Integer>> subsets(int[] nums) {this.res = new ArrayList<>();if(nums == null || nums.length == 0) return res;List<Integer> list = new ArrayList<>();res.add(new ArrayList<>(list));//加入特殊解[]backtrack(nums, 0, list);return res;}//回溯的递归实现public void backtrack(int[] nums, int start, List<Integer> list){for(int i = start; i < nums.length; i++){list.add(nums[i]);res.add(new ArrayList<>(list));backtrack(nums, i + 1, list);list.remove(list.size() - 1);}}
}

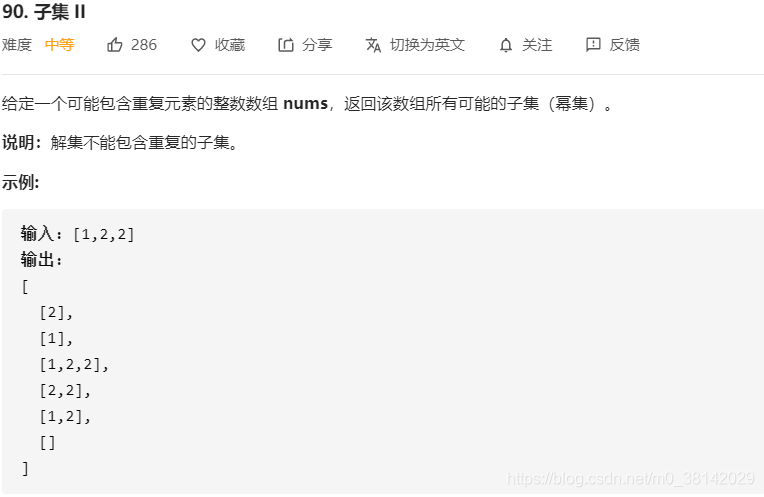
90.子集 II（含重复元素的解集去重）

题目链接：90.子集 II

分类：回溯法

题目分析：

这题和78.子集相比，数组可能包含重复元素，所以关键问题在于解集的去重。

但这题和第78题的去重有所不同，这题存在和78题同样的解集重复问题，同时数组的重复元素会带来另一个解集重复问题。

思路：回溯法

解集重复问题

1、进入下一层递归带来的重复解

例如：

nums=[1,2,2,2]，递归带来的重复解是:[1,2,2]和[1,2,2]。↑ ↑ ↑                       ↑ ↑      ↑ ↑ 
下标    1 2 3                       1 2      2 1
这是由于下一层递归没有从上一层递归所选数字的下一个数字开始而导致的。

通过修改for循环起点i=start，start作为递归函数参数传递给下一层的是start=i+1，从而可以解决这一个重复解问题。这个问题和78相同。

2、for循环带来的重复解问题

for循环就是替换当前位置的数字，

nums=[1,2,2,2]，for循环带来的重复解是:[1,2,2]和[1,2,2]，↑ ↑ ↑                           ↑ ↑      ↑ ↑ 1 2 3                           1 2      1 3
拿后面值相同的元素来替换掉当前的元素，带来的重复解。

通过拿for循环的第i个元素和前一个元素（第i-1个元素）比较，如果两元素值相同则不做替换，直接continue到for-i循环的下一轮。

这里要尤其注意：

一层递归的for循环框架如下：
for(int i = start; i < n; i++){list.add(nums[i])
}

在i == start时是向list末尾添加一个数字（即当前位置为空，需要填入数字而不是替换数字），i > start时才是对这个位置上的数字进行替换。（关键点，也是易忽略点，对for\递归实际意义的进一步补充！！！）

但这个方法的前提是nums数组是有序的，有序数组里相同的数字都相邻排列，如果不是有序的用nums[i]和nums[i-1]并不能找到所有的重复元素。所以要先对数组排序。

心得：（重要！）

这题加深了我对回溯法的理解.
之前的理解里：for循环就是替换当前位置上的数字，下一层递归是添加数字到下一个位置。
但更进一步地：for(int i = start; i < n; i++)中：当i == start时，做的是向当前的空位添加一个数字；当i > start时，才是对这个位置上的数字做替换。

实现代码

class Solution {List<List<Integer>> res;public List<List<Integer>> subsetsWithDup(int[] nums) {this.res = new ArrayList<>();if(nums == null || nums.length == 0) return res;List<Integer> list = new ArrayList<>();res.add(list);//加入[]Arrays.sort(nums);//数组排序backtrack(nums, 0, list);return res;}//回溯的递归实现public void backtrack(int[] nums, int start, List<Integer> list){for(int i = start; i < nums.length; i++){if(i > start && nums[i] == nums[i - 1]) continue;//关键点：i>start时才是对该位置数字的替换，i==start时list刚移出上一个数字，空出一个空位来list.add(nums[i]);res.add(new ArrayList<>(list));backtrack(nums, i + 1, list);list.remove(list.size() - 1);}}
}

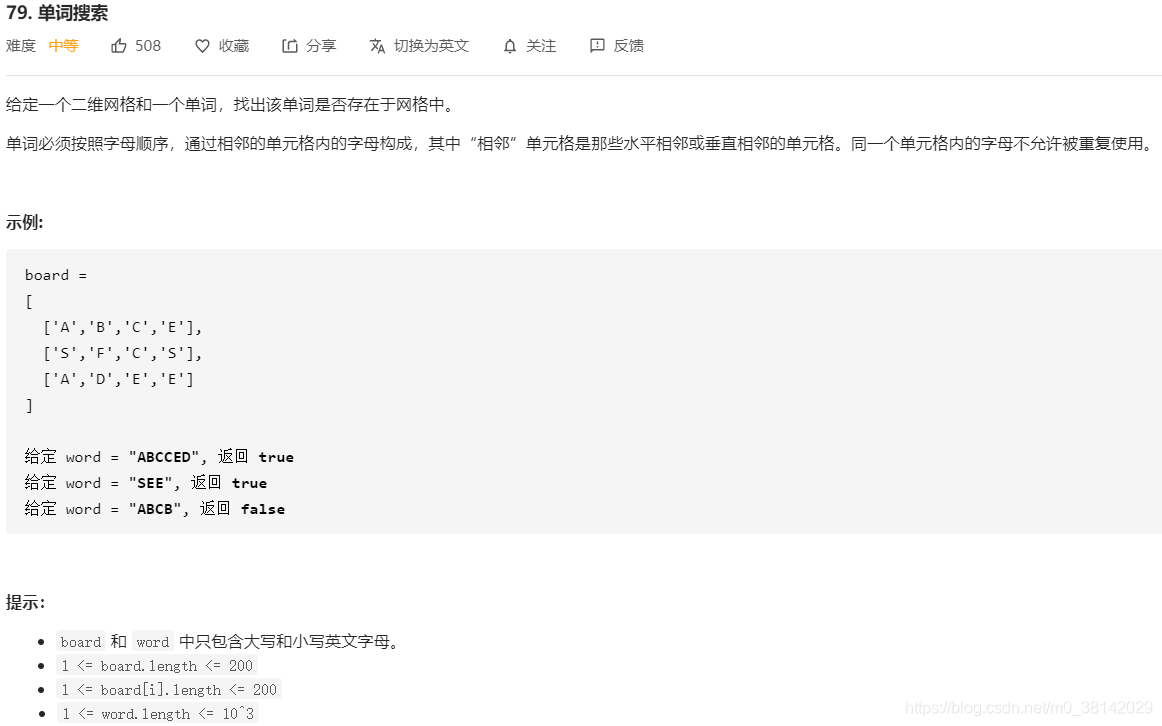
79.单词搜索（二维平面上回溯）

题目链接：79.单词搜索

分类：回溯法

题目分析

很明显是回溯题型，和之前的回溯题目不同点在于，这一题是在二维平面上使用回溯法，所以标记元素是否使用过的数组也要是二维的，对元素坐标的越界判断也要有做相应的修改。

思路：回溯法

• 状态变量：used二维数组标记元素是否使用过，depth表示构成的单词长度，当depth==word.length()时说明得到word相同的单词。
• 算法流程：
  选择一个起点，和word[0]比较，如果相同，则枚举起点的上下左右，选择和word下一个字符相同且没有被使用过的字符作为下一点，以此类推。

关键问题：

1、如何选择一个点的上下左右相邻节点？

设该点坐标为(i,j)，上=(i-1,j)，下=(i+1,j)，左=(i,j-1)，右=(i,j+1)，

2、选择相邻节点时要考虑哪些问题？

（1）最先考虑下标是否越界：

i - 1 >= 0 , i + 1 < board.length, j - 1 >= 0, j + 1 < board[0].length

（2）元素是否和word当前字符相同

board[i][j] == word.charAt(idx)

（3）元素是否被使用过

used[i][j] == true 表示使用过。

实现遇到的问题:

问题1：对上下左右邻接点的选取代码有错

输入：
[["a","b"],["c","d"]]
word = "abcd"
输出：true
预期：false

原因：两层for循环取一个点的上下左右，但我写成取一个点的周围8个邻接点了。
修改前代码：

    for(int i = -1; i <= 1; i++){for(int j = -1; j <= 1; j++){if(i == j) continue;...}}

只排除了九宫格里中间那个点。

修改后代码：

    for(int i = -1; i <= 1; i++){for(int j = -1; j <= 1; j++){if(Math.abs(i - j) > 1) continue;...}}

排除了对角线上的4个点。这些点的统一特点就是坐标之差的绝对值>1

问题2：没有检验word的最后一个字符

例如：
[["a","a","a","a"],["a","a","a","a"],["a","a","a","a"],["a","a","a","a"],["a","a","a","b"]]
word = "aaaaaaaaaaaaaaaaaaaa" ，
输出：true
预期：false

之前的版本里对word的最后一个字符没有检验。修改前代码见提交记录。

实现代码

class Solution {public boolean exist(char[][] board, String word) {//特殊用例if(board.length * board[0].length < word.length()) return false;//标记元素是否使用过boolean[][] used = new boolean[board.length][board[0].length];//依次取board上的每个节点作为起点调用回溯函数寻找有效的解for(int i = 0; i < board.length; i++){for(int j = 0; j < board[i].length; j++){if(backtrack(board, word, used, 0, i, j)) return true;}}return false;}//回溯函数:对以(i,j)为起点的寻找过程public boolean backtrack(char[][] board, String word, boolean[][] used, int depth, int x, int y){if(depth == word.length() - 1){return board[x][y] == word.charAt(depth);}if(board[x][y] == word.charAt(depth)){used[x][y] = true;//取当前节点的上下左右相邻节点for(int i = -1; i <= 1; i++){//x+i的越界判断if(x + i < 0 || x + i >= board.length) continue;for(int j = -1; j <= 1; j++){//排除对角线上的邻接点if(Math.abs(i - j) != 1) continue;//y+j的越界判断if(y + j < 0 || y + j >= board[0].length) continue;if(used[x + i][y + j]) continue;if(backtrack(board, word, used, depth + 1, x + i, y + j)) return true;}}used[x][y] = false;}return false;}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！