定义

1.假如一条边有权重，或者称为距离，要求某一个点（称为源点）到某个点的最短距离。

实现

1.无权图广度优先算法

这个算法的思路是在当前长度为i的时候，访问所有距离源点为i且之前没有被遍历的点。可以确定这些点离源点的最短距离就是i，否则之前就应该被经过了。

因此与其相邻未被经过的点的最短距离是i+1。

这个算法用距离无穷表示之前没有遍历，又用kown来表示，感觉多写了。

void Unweighted( Table T )
{   int  CurrDist;Vertex  V, W;for ( CurrDist = 0; CurrDist < NumVertex; CurrDist ++ ) {for ( each vertex V )if ( !T[ V ].Known && T[ V ].Dist == CurrDist ) {T[ V ].Known = true;for ( each W adjacent to V )if ( T[ W ].Dist == Infinity ) {T[ W ].Dist = CurrDist + 1;T[ W ].Path = V;} /* end-if Dist == Infinity */} /* end-if !Known && Dist == CurrDist */}  /* end-for CurrDist */
}

2.对上述算法的改进，思路是将未经过的一个点入队列，每次取出一个点,将该点加入到经过的序列中，然后将与这个点相邻的且之前未经过的点距离=当前点+1并入队列。

void Unweighted( Table T )
{   /* T is initialized with the source vertex S given */Queue  Q;Vertex  V, W;Q = CreateQueue(NumVertex );  MakeEmpty( Q );Enqueue( S, Q ); /* Enqueue the source vertex */while ( !IsEmpty( Q ) ) {V = Dequeue( Q );T[ V ].Known = true; /* not really necessary */for ( each W adjacent to V )if ( T[ W ].Dist == Infinity ) {T[ W ].Dist = T[ V ].Dist + 1;T[ W ].Path = V;Enqueue( W, Q );} /* end-if Dist == Infinity */} /* end-while */DisposeQueue( Q ); /* free memory */
}

3.带权图Dijkstra’s Algorithm

思路是选择当前距离最小的未经过的点w，加入到经过的序列中，遍历并更新与它相邻且未经过的点v的距离（本来v与源点不相邻或者距离更大，但是有一条更短的路径s->w->v）

void Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{int collected[MaxVertexNum];Vertex V, W;for ( V=0; V<Graph->Nv; V++ ) {path[V] = -1;dist[V] = Graph->G[S][V];collected[V] = false;}dist[S] = 0;collected[S] = true;while (1) {V = FindMinDist( Graph, dist, collected );/*每次找一个最小的未经过的点，经过它*/if ( V==ERROR ) break;collected[V] = true;for( W=0; W<Graph->Nv; W++ )/*遍历所有与该点相邻的点*/if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {/*如果相邻，并且没有经过过，则看会不会更近一点*/if ( dist[W]>dist[V]+Graph->G[V][W] ) {path[W] = V;dist[W] = dist[W]+Graph->G[V][W];}}} /* end while */
}

4.带负权图

void  WeightedNegative( Table T )
{   /* T is initialized by Figure 9.30 on p.303 */Queue  Q;Vertex  V, W;Q = CreateQueue (NumVertex );  MakeEmpty( Q );Enqueue( S, Q ); /* Enqueue the source vertex */while ( !IsEmpty( Q ) ) {V = Dequeue( Q );for ( each W adjacent to V )if ( T[ V ].Dist + Cvw < T[ W ].Dist ) {T[ W ].Dist = T[ V ].Dist + Cvw;T[ W ].Path = V;if ( W is not already in Q )Enqueue( W, Q );} /* end-if update */} /* end-while */DisposeQueue( Q ); /* free memory */
}

AOE定义

AOE：(activitity in edge)边表示事件以及完成所需要的时间，结点表示完成该事件。

EC:最早达到该结点的时刻，前提是完成所有在这之前的事件。

LC:最迟达到该节点的时刻

计算EC,LC

EC是从头开始到该事件结束，所有路径之和的最大值
LC是从尾开始最小到该事件结束，总时间减去LC的最小值。

v,w松弛时间= LC[w] - EC[v] - D(v,w)

Critical Path:从头到尾，所有结点LC=EC的

题目

1.The following figure shows the AOE network of a project with 8 activities. The earliest and the latest completion times of the activity d are __, respectively.

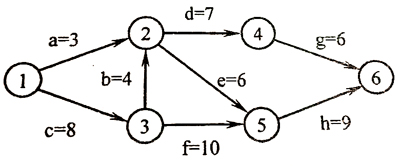
问d的LC和LE，LE是8+4+7=19，LC是27-6=21，可是答案是12/14都减了d的时长，不是很清楚。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！