第一行一个正整数 k ，表示有 k  次询问。

接下来 k  行，第 i  行三个正整数 ni , di , ei。

输出 k kk 行，每行两个正整数 pi , qi 表示答案。

为使输出统一，你应当保证 pi ≤ qi。

如果无解，请输出 NO。

10
770 77 5
633 1 211
545 1 499
683 3 227
858 3 257
723 37 13
572 26 11
867 17 17
829 3 263
528 4 109

2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88

【数据范围】

以下记 m = n − e × d + 2。

保证对于 100% 的数据，1 ≤ k ≤ 10^5 ，对于任意的 1 ≤ i ≤ k ，1 ≤ ni ≤ 10^18 ，1 ≤ ei × di≤10^18
，1 ≤ m ≤ 10^9。

思路一：

分析：

可以用两层for循环来枚举

代码：略

优化的话，从1到sqrt(n),再省掉一层for循环。

代码：

70分

#include 
using namespace  std;struct nod{long long x,y,z;
}a[100010];int n;int main(){scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%lld %lld %lld",&a[i].x,&a[i].y,&a[i].z);}for(int i=1;i<=n;++i){bool f=true;for(long long x=1;x*x<=a[i].x;++x){if(a[i].x%x!=0){continue;}long long ans=a[i].x/x;if((x-1)*(ans-1)+1==a[i].y*a[i].z){if(ans*x==a[i].x){f=false;cout<< min(x,ans) << " " << max(x,ans) << endl;break;}}}if(f==true){cout<< "NO" << endl;}}return 0;
}

思路二：

背景：

想一想，如果你有一个计算器，只可以用+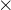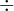，-，，，来求是多少？

可以先看1—300的中间数——150，看看是大于还是小于，还是等于，大于在1-150之间的中间数再看；小于的话从150-300的中间数看；等于就是解，当然解有可能是小数。

你看：二分性质呀！！！！！！！！！！！！！！！！！（此处省略个！）

分析：

化简后二分求解。
化简得：n = p × q , m = p + q。
当两数的和为定值时，在区间[1, m / 2]内，p越大乘积就越大。
因此可以两分求解。

代码：

100分

#include 
using namespace std;int main(){long long x,y,z,m,k;cin>>k;for(int i=1;i<=k;++i){cin>>x>>y>>z;m=x-y*z+2;long long l=0,r=m/2+1;while(l+1