数学(三):高斯消元、求组合数
高斯消元
原理:

例题:高斯消元解线性方程组
输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 mm 个方程 nn 个未知数的线性方程组示例:
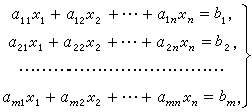
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1个实数,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出 Infinite group solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100
所有输入系数以及常数均保留两位小数,绝对值均不超过 100。
输入样例:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例:
1.00
-2.00
3.00解题:

#include
#include
#include using namespace std;const int N=110;
const double eps=1e-6;int n;
double a[N][N];int gauss()
{int c,r;//c:枚举的哪一列,r:表示哪行for(c=0,r=0;cfabs(a[t][c]))t=i;if(abs(a[t][c])=c;i--) a[r][i]/=a[r][c];//把该列第一个数变成1,倒着来for(int i=r+1;ieps)for(int j=n;j>=c;j--)a[i][j]-=a[r][j]*a[i][c];r ++;}if(reps)return 2;//无解return 1;//有无穷解 }for (int i = n - 1; i >= 0; i -- )//倒着把方程消一边for (int j = i + 1; j < n; j ++ )a[i][n] -= a[j][n] * a[i][j];return 0;//有唯一解
}int main()
{cin>>n;for(int i=0;i>a[i][j];int t=gauss();if(t ==0){for(int i=0;i 求组合数
1. 10万组 1<=b<=a<=2000 递归
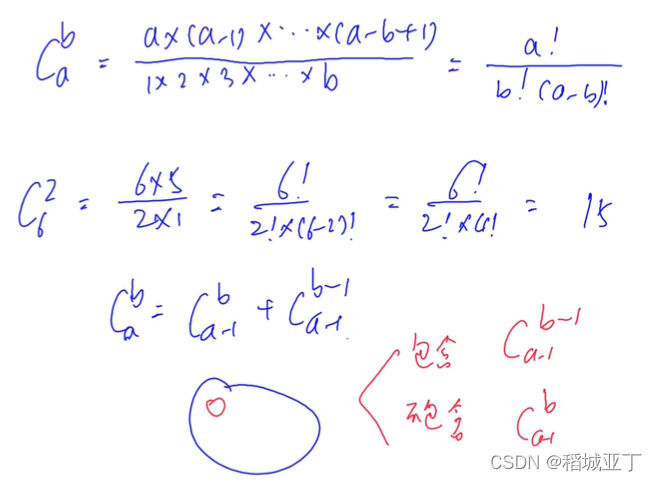
例题:求组合数 I
给定 n 组询问,每组询问给定两个整数 a,b请你输出 Cbamod(109+7)的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000
1≤b≤a≤2000
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1解题代码:
#include
#include using namespace std;const int N=2010,mod=1e9+7;int c[N][N];void init()
{for(int i=0;i 2. 1万 1<=b<=a<=10^5 预处理
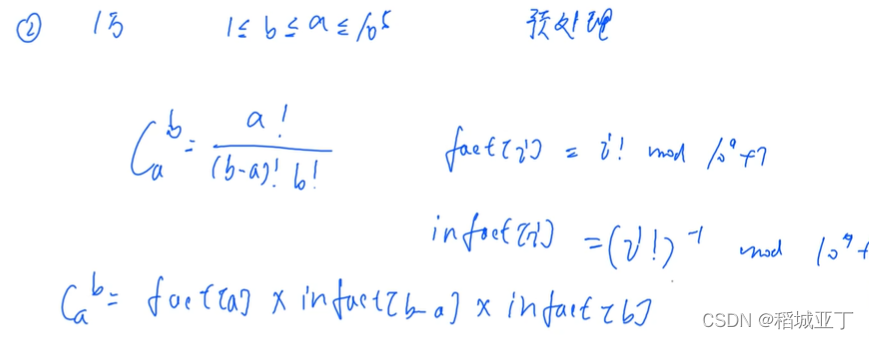
例题:求组合数 II
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Cbamod(109+7)的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000
1≤b≤a≤105
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
解题:
#include
#include using namespace std;const int N=100010,mod=1e9+7;typedef long long LL;int fact[N],infact[N];int qmi(int a,int k,int p)//快速幂求逆元
{int res=1;while(k){if(k&1) res=(LL)res*a%p;a=(LL)a*a%p;k>>=1;}return res;
}int main()
{fact[0]=infact[0]=1;//0的阶乘都是1for(int i=1;i 3. 20组 1<=b<=a<=10^18 1<=p<=10^5 卢卡斯定理


例题:求组合数 III
给定 n 组询问,每组询问给定三个整数 a,b,p,其中 p 是质数,请你输出 CbamodpCabmodp 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a,b,p
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤20
1≤b≤a≤1018
1≤p≤105
输入样例:
3
5 3 7
3 1 5
6 4 13
输出样例:
3
3
2解题:
#include
#include using namespace std;typedef long long LL;int p;int qmi(int a,int k)
{int res=1;while(k){if(k&1) res=(LL) res*a%p;a=(LL) a*a%p;k>>=1;}return res;
}int C(int a,int b)
{int res=1;for(int i=1,j=a;i<=b;i++,j--){res=(LL)res*j%p;res=(LL)res*qmi(i,p-2)%p;}return res;
}int lucas(LL a,LL b)
{if(a>n;while(n--){LL a,b;cin >>a>>b>>p;cout < 4. 结果很大,需要使用高精度计算

例题:求组合数 IV
输入 a,b,求 Cba的值。
注意结果可能很大,需要使用高精度计算。
输入格式
共一行,包含两个整数 a 和 b。
输出格式
共一行,输出 Cba 的值。
数据范围
1≤b≤a≤5000
输入样例:
5 3
输出样例:
10解题:
#include
#include
#include using namespace std;const int N=5010;int primes[N],cnt;
int sum[N];
bool st[N];void get_primes(int n)
{for(int i=2;i<=n;i++) {if(!st[i]) primes[cnt ++]=i;for(int j=0;primes[j]<=n/i;j++){st[primes[j]*i]=true;if(i%primes[j]==0) break;}}
}int get(int n,int p) //存n的阶乘里面包含p的个数
{int res=0;while(n){res+=n/p;n/=p;}return res;
}vector mul(vector a,int b)
{vector c;int t=0;for(int i=0;i>a>>b;get_primes(a);//先预处理除a里面所有的质数for(int i=0;i res;res.push_back(1);for(int i=0;i=0;i--) printf("%d",res[i]);puts("");return 0;} 5. 卡特兰数
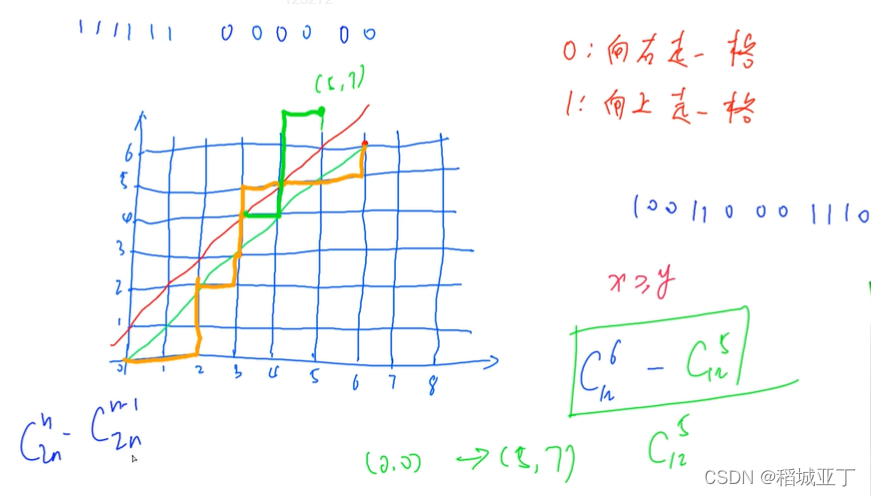
例题:满足条件的01序列
给定 n 个 0 和 n 个 1,它们将按照某种顺序排成长度为 2n的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。
输出的答案对 109+7 取模。
输入格式
共一行,包含整数 n。
输出格式
共一行,包含一个整数,表示答案。
数据范围
1≤n≤105
输入样例:
3
输出样例:
5解题:

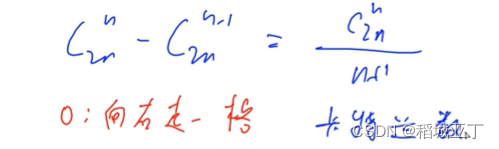
#include
#include using namespace std;typedef long long LL;
const int mod=1e9+7;//快速幂
int qmi(int a,int k,int p)
{int res=1;while(k){if(k&1) res=(LL)res*a%p;a=(LL)a*a%p;k>>=1;}return res;
}int main()
{int n;cin>>n;int a=2*n,b=n;int res=1;for(int i=a;i>a-b;i--) res=(LL)res*i%mod;for(int i=1;i<=b;i++) res=(LL)res*qmi(i,mod-2,mod)%mod;res=(LL)res*qmi(n+1,mod-2,mod)%mod;cout< 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!