面试针对性准备（一）

过往的项目经历

参考书：
《行为统计学基础（第九版）》人民大学出版社2007
豆瓣链接
《时间序列与多元统计分析》上海交通大学出版社2016

时间序列分析

1 数据分析流程
产品/需求：课程设计中需要解决管理统计学与数据挖掘的一个相关问题。

整理寻找问题点：借助以往政府开放数据调研的经验，选题《哈尔滨市地区生产总值时间序列分析》

描述性统计观察数据表象：通过折线图判断变化趋势
（也可以计算各种描述性统计量，但是在这种预测的过程中我更喜欢直接看可视化的图形）

标注变化：趋势图指引曲线拟合方向->进一步判断属于二次曲线还是指数曲线
（二次曲线它的二阶差分是一个定值，指数曲线它的函数值环比是一个定值）

多维分析
（多指标）交叉分析
（上述两步在该分析项目中没有涉及）

预测趋势：
求解指数曲线->化曲为直（使用EXCEL中的LOG10函数）->SPSS 进行一元线性回归拟合与检验
（
拟合过程
1 使用PEARSON系数判断有显著的相关性（r值）

PEARSON系数
1 用于区间或者比率数据
2 解释相关系数
r
相关系数的大小（联系的强弱）和符号（正向/反向）
两个随机变量是否相互联系，它们以何种方式相互联系
R²

相关系数的重要性依赖于研究的种类。
在解释统计量时，要考虑数据收集的环境和基于统计结论所做出的结论。

相关系数的显著性：随机因素导致结果的概率

Spearman序列相关系数
用于排序数据或者有序数据

2 回归拟合线性方程，同时再次确认数据是否适合做线性回归：
-就模型残差进行DurbinWatson检验，用于判断残差是否独立，作为一个基础条件来判断
-直方图
-正态概率图）
（
评价过程
1 R²为判定系数，一般认为需要大于 60%，用于判定线性方程拟
合优度的重要指标，体现了回归模型解释因变量变异的能力，越接近
1 越好。
2 方差分析F和sig两个值
F值为方差分析的结果，对整个回归方程的总体检验，指的是整个回归方程有没有使用价值（与随机瞎猜相比）。从F值的角度来讲：F的值是回归方程的显著性检验，表示的是模型中被解释变量与所有解释变量之间的线性关系在总体上是否显著做出推断。
其F值对应的Sig值小于0.05就可以认为回归方程是有用的

）
（下面两步在该分析项目中没有涉及）
生成（一个运营或者产品的）策略
推动落地

复盘效果
拟合曲线的预测效果不理想——
1 现有数据更换模型：多元统计分析（第一产业、第二产业、第三产业等作为因变量）
2 从其他角度收集数据与资料，寻找影响地区生产总值的因素

3 时间序列分析
处理与时间有关系的数据

功能：描述现象、事物随时间推移的变化规律性；预测。

特点：样本变量的独立同分布条件常常不满足，因为前后现象之间常常是有联系的。时间具有一去不复返性，时间序列数据一般不能通过重复实验取得。

建模主要做三件事：
选择合适的模型
对选定模型进行参数估计（矩估计、MLE、最小二乘法；一些主要应用模型特殊性的新方法）
对建立好的模型进行有效性检验

一些常见的时间序列模型可以看作回归模型，只是条件可能不同

时间序列分析步骤与统计软件SPSS的应用

步骤
1 预处理
绘制时间序列图，由图形结合序列背景，考察独立、平稳、趋势，周期情况，若有趋势项或周期项，则对原始数据作差分（Y_t = X_t - X_t-T，T为周期），直到近似平稳（平稳时的散点图应显示点在一条水平线上下摆动，左中右各群点的上下波动范围没有明显差异，并且不带有明显的周期性）为止
2 计算样本自协方差函数或者样本自相关函数，并计算样本偏相关函数，绘制相应的图像。
3 建模
（1）对预处理后的平稳序列用自相关、偏相关的截尾性质确定拟合类型（AR\MA\ARMA）
（2）定阶、参数估计、拟合检验
（3）若检验不通过则分析原因，调整阶数重新估计和检验

实践
导入EXCEL数据
对当前语言环境而言文本值过长

编辑“变量视图”中的数据属性
个案与属性

（下面开始对应上面的步骤依次实现）
预处理
绘制时间序列图(横轴为序号，纵轴为要观察的变量-地区生产总值)
分析->预测->序列图
如图所示，该序列不符合使用时间序列分析的基础

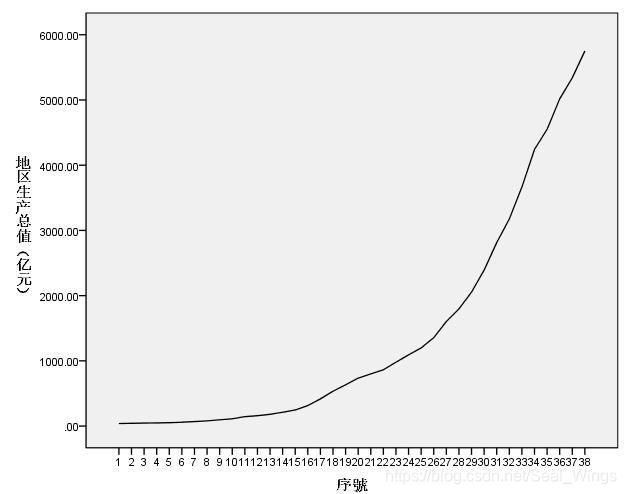
故利用已有数据转向n元统计分析
转回到我曾经的实验报告内容

4 多元统计分析

多元统计分析中常用的统计量
样本均值向量、样本协方差矩阵

聚类分析
（1）类型
样品聚类-个体-距离
变量聚类-个体的数量特征-相似系数

（2）系统聚类法<>分类法
逐步将相似程度好的类合并在一起，最终所有样本都合并为一类；再画出聚类图决定分出多少类，每类各有什么样品。

（3）k-means
欧式距离

（4）有序样品的聚类

判别分析
把考察的事物已经分成了若干类，如何根据一个带判断事物的特征，判别它属于哪一类
（1）距离判别法
欧式距离的缺陷——
与正太分布的3sigma原则的冲突
计算值受单位的影响
↓
马氏距离

（2）Fisher判别法
通过将多维数据向某个方向投影，投影的原则是将总体和总体尽可能地拉开，即投影后同一个总体地成员要靠得近，不同总体的成员要离得远。

（3）Bayes判别法
要判断就存在错判的可能，该方法使错判的可能达到最小。

主成分分析
实际问题研究中常常要涉及多项指标，在很多情况下，不同指标之间有一定的线性相关性。（上述两点内容增加了分析问题的复杂性）

设法将原指标综合成一组新的不相关的指标——新指标应尽可能多地含有原指标的信息，并且所含原指标信息的多少可以依次排队，可以选用含信息多的一部分新指标来代替原有指标。
——处理降维的一种方法

主成分分析单独使用。
主成分分析与其他分析结合：主成分回归分析。

（1）总体主成分
取原来k个指标的线性组合作为新的综合指标Z
↓
希望它尽可能多的反映原来指标的信息
↓
方差越大，包含信息越多
↓
第一主成分之后考虑第二主成分
↓
第一主成分的信息就不需要再包含了

（2）样本主成分

因子分析

主成分分析的一种推广，一种降维、简化数据的技术。

目的是找出少数几个变量（公因子），去描述具有相关性的多个变量，即能反映原来多个变量的主要信息。

典型相关分析

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！