【季节性预测法 - 时间序列分解法】利用excel进行复合型时间序列的分解预测
希望我整理的内容对路过的你有所帮助,点赞或评论,都是相互的鼓励~
【问题】根据下图中某啤酒生产企业2010-2015年各季度的销售量数据,预测2016年各季度产量
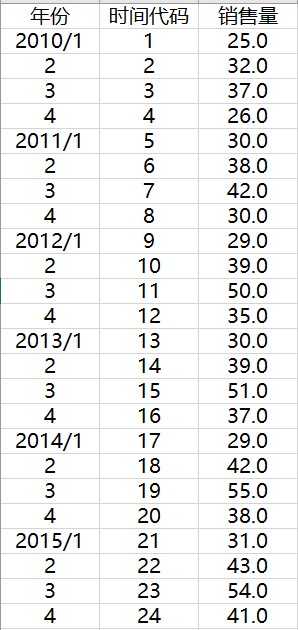
1. 绘制时间序列图,观察啤酒销售量的构成要素
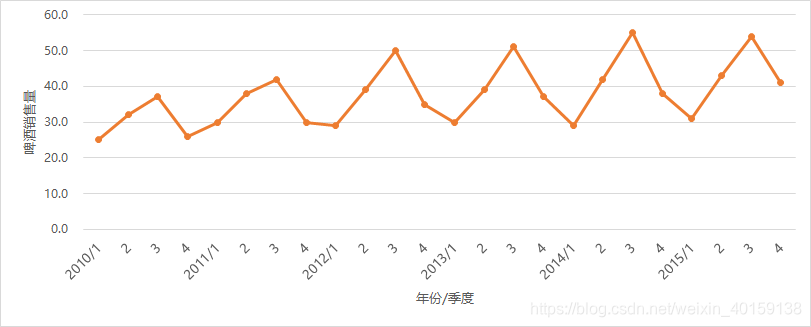
从上图可以明显看出,啤酒销售量具有明显季节成分,而且后面年份销量比前面年份高,因此其中含有趋势成分,但其周期性难以判断。可以认定啤酒销售量序列是一个含有季节性成分和趋势成分的时间序列。
2. 确定季节成分,计算季节指数
2.1 计算移动平均值
-- 对于季节数据,从2010年1季度开始,每4个季度计算4项移动平均,如:
| 年份/季度 | 4项移动平均计算 | 4项移动平均值 | 4项移动平均 对应季度 |
| 2010/1, 2010/2,2010/3, 2010/4 | (25.0+32.0+37.0+26.0) / 4 | 30.00 | 2.50 |
| 2010/2,2010/3, 2010/4, 2011/1 | (32.0+37.0+26.0+30.0) / 4 | 31.25 | 3.50 |
| 2010/3, 2010/4, 2011/1, 2011/2 | (37.0+26.0+30.0+38.0) / 4 | 32.75 | 4.50 |
| … | … | … | … |
这里出现的问题是,计算出的4项移动平均,没有对应着具体的某个季度,而是在季度之间!
为了解决这个问题,需要进行中心化处理。
-- 对计算结果进行中心化处理,也就是再进行一次二项移动平均,得出中心化移动平均值CMA。
这样处理之后,移动平均值便对应具体季度。思路如下(给我自己做的图点赞❤):
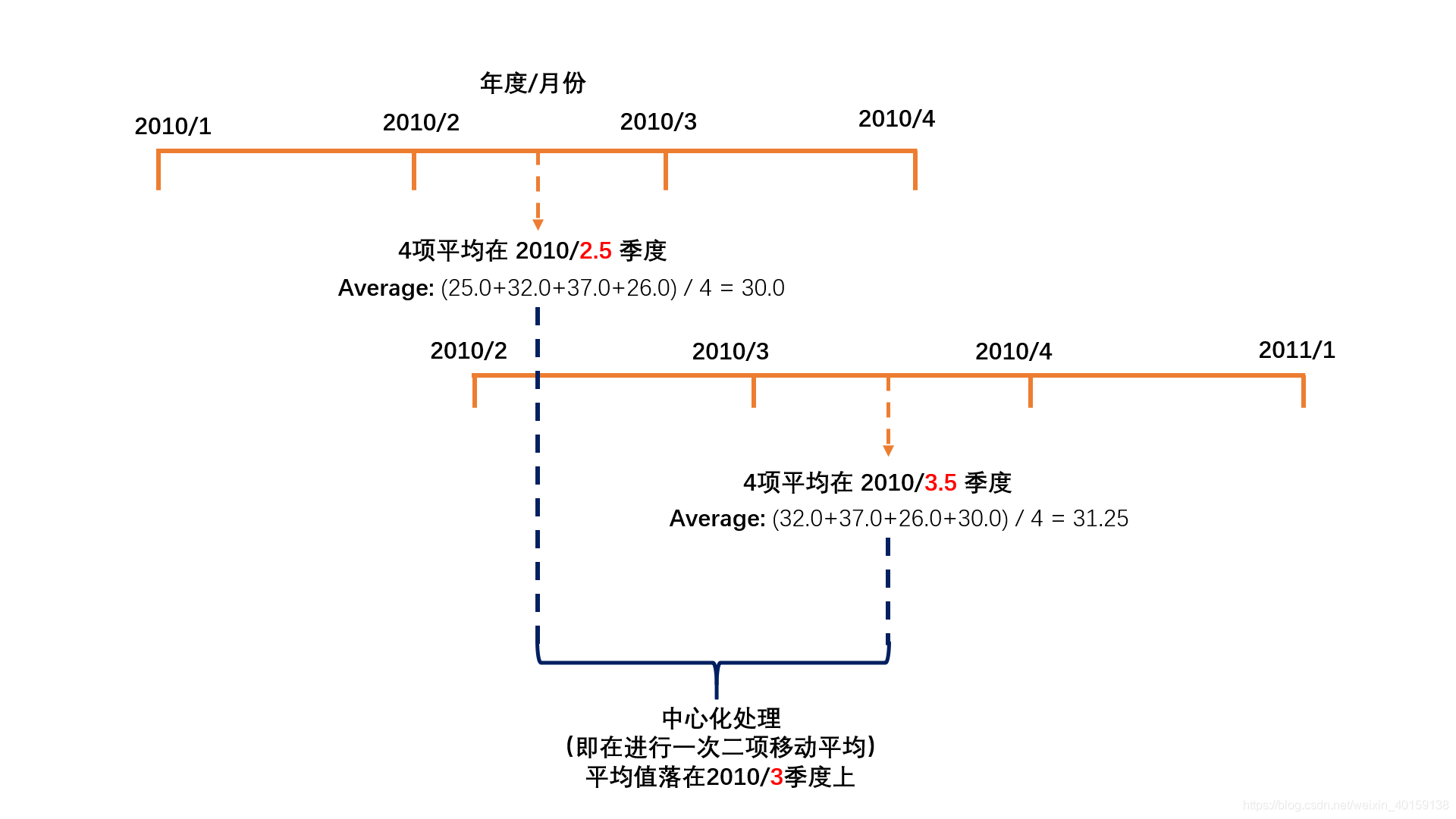
按照上述思路,计算出的中心化移动平均值CMA情况如下:
| 年份 | 时间代码 | 销售量 | 4项移动平均 | 中心化移动平均值 CMA |
| 2010/1 | 1 | 25.0 | ||
| 1.5 | ||||
| 2 | 2 | 32.0 | ||
| 2.5 | 30.000 | |||
| 3 | 3 | 37.0 | 30.625 | |
| 3.5 | 31.250 | |||
| 4 | 4 | 26.0 | 32.000 | |
| 4.5 | 32.750 | |||
| 2011/1 | 5 | 30.0 | 33.375 | |
| 5.5 | 34.000 | |||
| 2 | 6 | 38.0 | 34.500 | |
| 6.5 | 35.000 | |||
| 3 | 7 | 42.0 | 34.875 | |
| 7.5 | 34.750 | |||
| 4 | 8 | 30.0 | 34.875 | |
| 8.5 | 35.000 | |||
| 2012/1 | 9 | 29.0 | 36.000 | |
| 9.5 | 37.000 | |||
| 2 | 10 | 39.0 | 37.625 | |
| 10.5 | 38.250 | |||
| 3 | 11 | 50.0 | 38.375 | |
| 11.5 | 38.500 | |||
| 4 | 12 | 35.0 | 38.500 | |
| 12.5 | 38.500 | |||
| 2013/1 | 13 | 30.0 | 38.625 | |
| 13.5 | 38.750 | |||
| 2 | 14 | 39.0 | 39 | |
| 14.5 | 39.250 | |||
| 3 | 15 | 51.0 | 39.125 | |
| 15.5 | 39.000 | |||
| 4 | 16 | 37.0 | 39.375 | |
| 16.5 | 39.750 | |||
| 2014/1 | 17 | 29.0 | 40.250 | |
| 17.5 | 40.750 | |||
| 2 | 18 | 42.0 | 40.875 | |
| 18.5 | 41.000 | |||
| 3 | 19 | 55.0 | 41.250 | |
| 19.5 | 41.500 | |||
| 4 | 20 | 38.0 | 41.625 | |
| 20.5 | 41.750 | |||
| 2015/1 | 21 | 31.0 | 41.625 | |
| 21.5 | 41.500 | |||
| 2 | 22 | 43.0 | 41.875 | |
| 22.5 | 42.250 | |||
| 3 | 23 | 54.0 | ||
| 23.5 | ||||
| 4 | 24 | 41.0 |
2.2 计算季节比率
销售量 同 中心化移动平均值CMA 的比值 = 季节比率
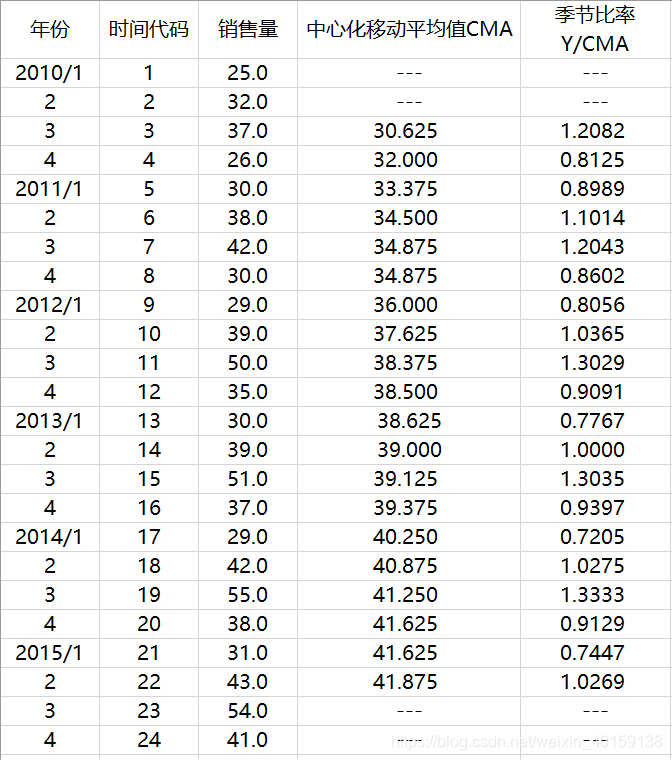
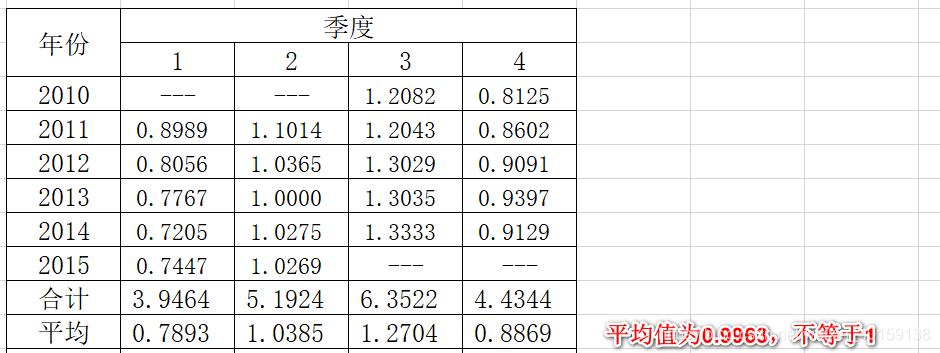
在乘法模型中,季节指数是以其平均数等于100%为条件而构成的,它反映了某一季度的数值占全年平均数值的大小。
这里,我们计算出的四个季节比率的平均数为0.9963,不等于1,需进行调整。
2.3 季节指数调整
将每个季节比率的平均值除以四个季节比率的总平均值,得到季节指数
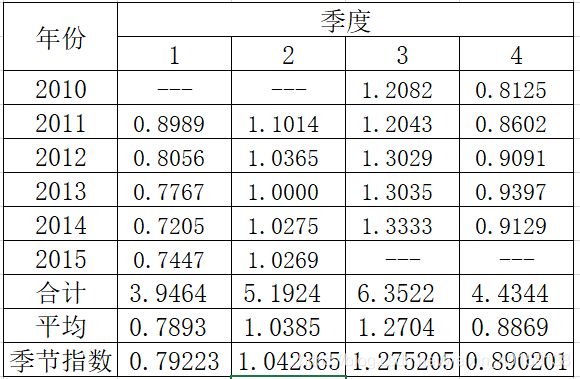
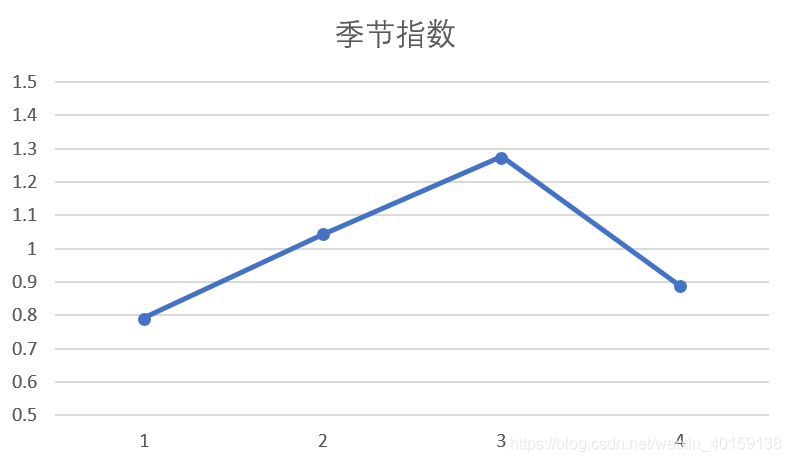
从季节指数变动图可以看出,啤酒销售量的旺季是3季度,淡季是1季度。
3. 分离季节成分
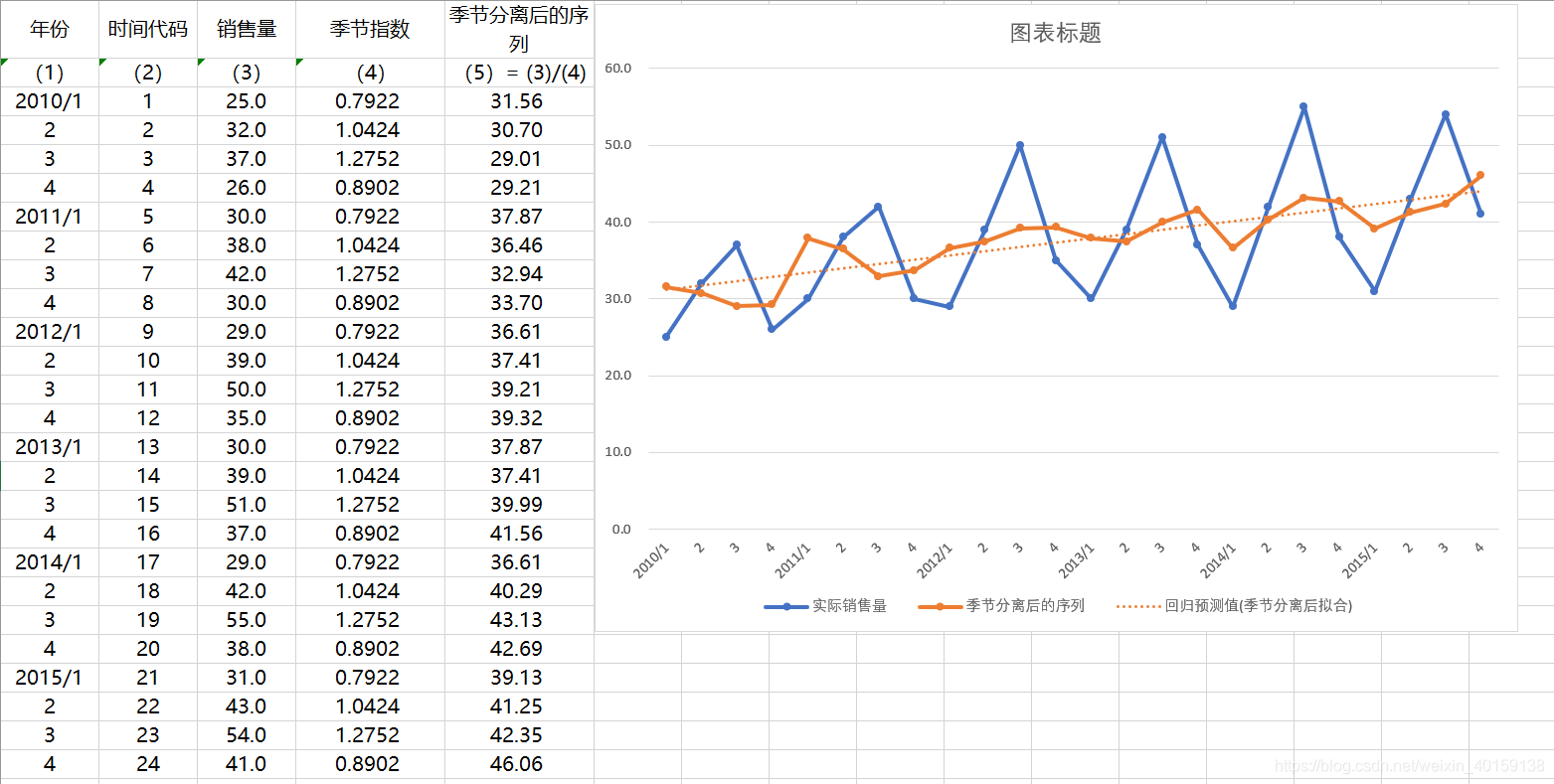
将实际销售量分别除以相应的季节指数,将季节成分从时间序列中分离出去,得到分离季节成分的序列。
4. 建立预测模型
剔除季节成分后,可以观察到啤酒销量有明显的线性增长趋势。用一元线性模型进行回归分析,得到分离季节因素后的序列对应的线性趋势方程为:
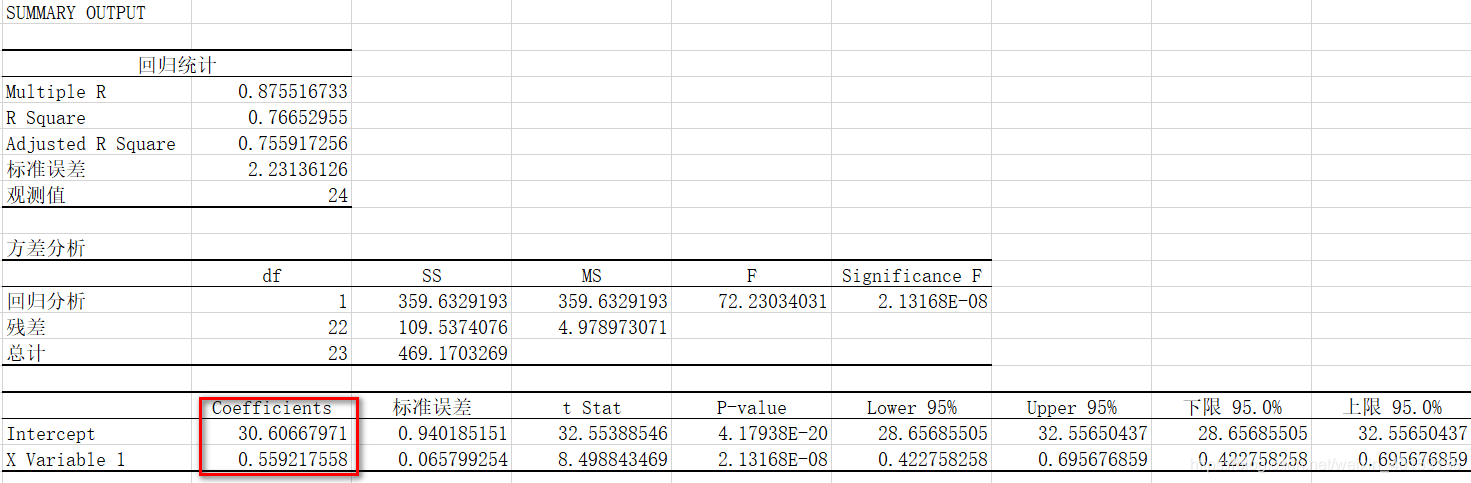
5. 预测2016年度销量
根据趋势方程,带入t=25,可以求得2016年1季度销售量(不含季节因素),再乘以对应的季度指数,就可以求得最终的销售量预测值。
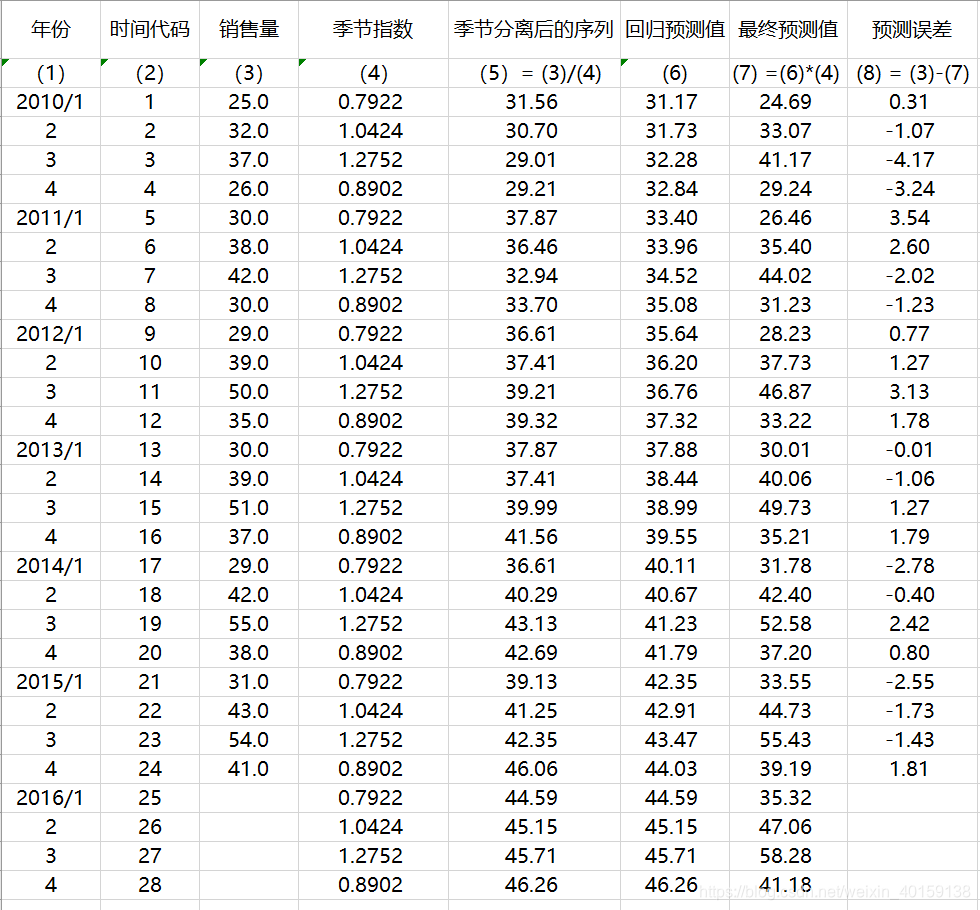
将实际销售量和最终预测值进行做图比对,可以看出,预测效果非常好。
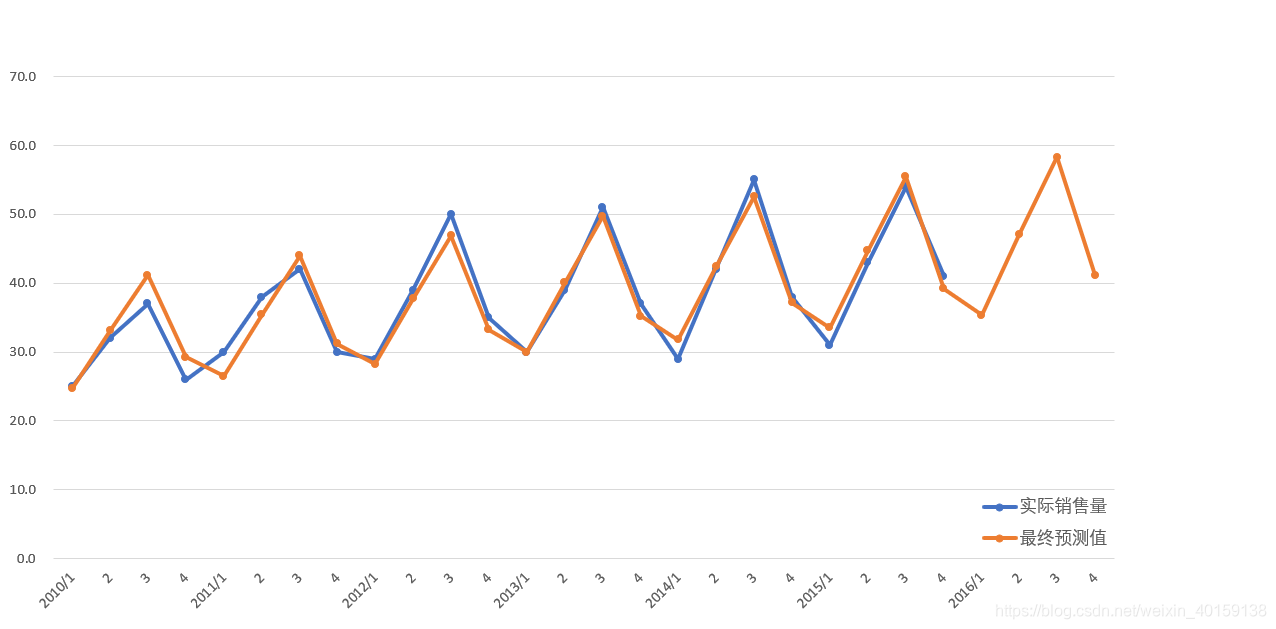
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!