文献摘录：

在修复算法中

①Greedy只能修改规则的右值。Bohannon P, Fan W, Flaster M et al (2005) A cost-based model and effective heuristic for repairing constraints by value modification. In: Özcan F (ed) Proceedings of SIGMOD, ACM, Baltimore,MD, pp 143–154

②Llunatic根据候选值的频率修复规则两边的属性值。 Geerts F, Mecca G, Papotti P et al (2013) The LLUNATIC data-cleaning framework. PVLDB 6(9):625–636

工作：

不同实体的不一致性？

摘要：

数据修复方法包含真值发现和基于规则的修复。真值发现用于解决多数据源同一实体间的冲突，基于规则的数据修复方法利用完整性约束来解决不同实体之间的不一致性。本文用函数依赖检测违规，并根据“可靠源”进行发现和修复错误。通过建模迭代框架，判断谁是“可靠源”。显然根据”可靠源“会导致其他的不一致，方法不太好。

介绍：

        主要针对多数据源描述同一实体的冲突以及不同实体间的“不一致”。解决前者的技术成为“真值发现”，其中之一是将包含更多正确值的数据源当作“可靠源”，当存在冲突时，以可靠源的数据为基准。多数据源不一致的问题通过规则检测和修复（考虑最小代价）。

前期工作

        通过规则修复时应注意规则的左右部都能够恢复，而不是只能恢复右部。

对修复代价的定义：

方法论

独立约束的修复框架

        主要采用数据修复和数据聚合，先数据修复再数据聚合。先数据聚合会导致损失一些正确值.

1、解决独立约束：

        在公共属性上没有重叠，解决一个属性不会影响其他的约束。X→Y，通过XY的结合解决修复错误。但结合可能有多种可能，所以采用“Global Pattern Selection 全局模式选择”。

2、全局模式：

        函数依赖左部的全部可能性。以该表为例，已知知道规则(Street,AC→ZIP)，其中部分元组的左部相同，可以分为三个，分别是(16th ave,720)、(38th ave,720)、(38th ave,303)。将每种左部选出一个元组，构成全局模式。

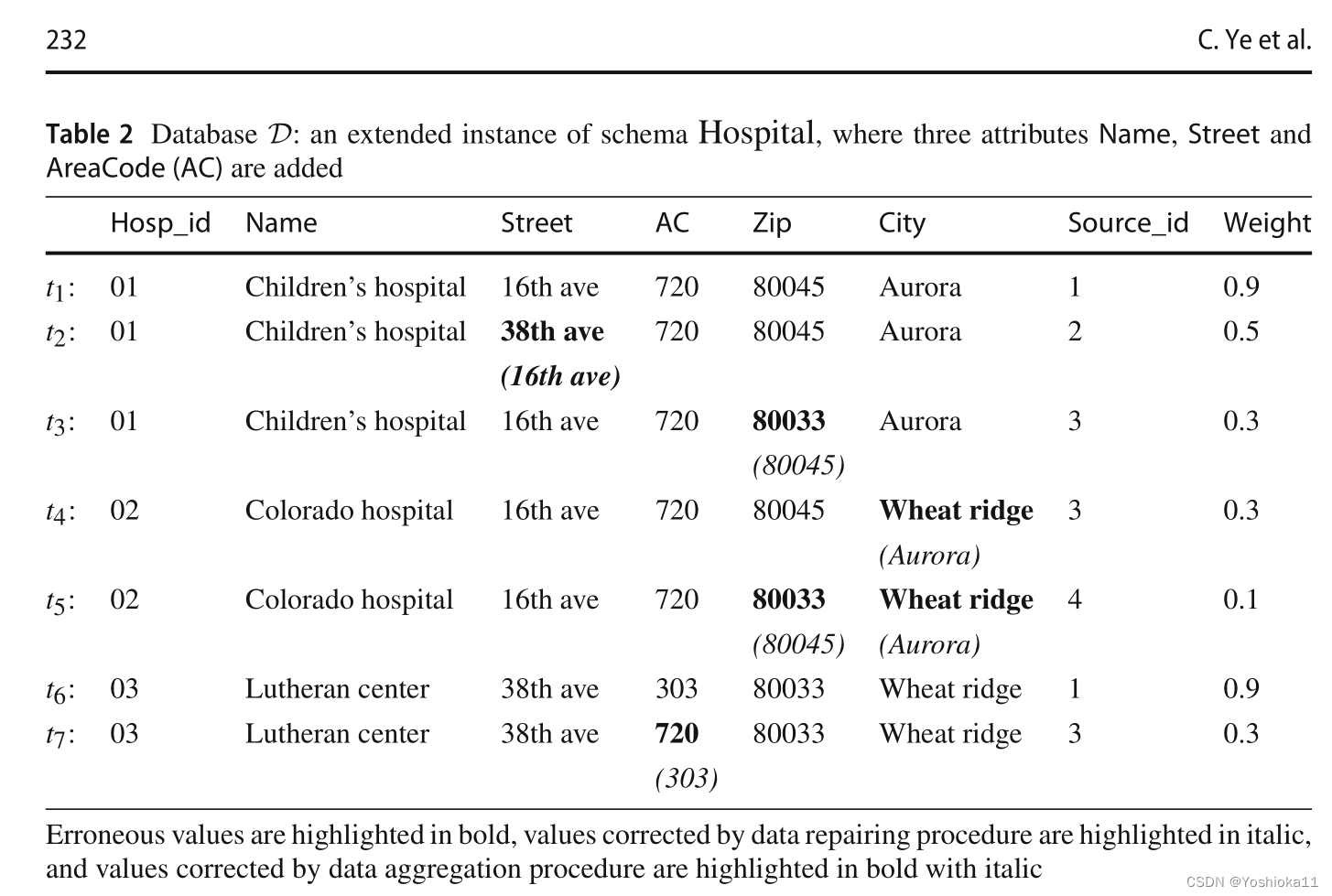
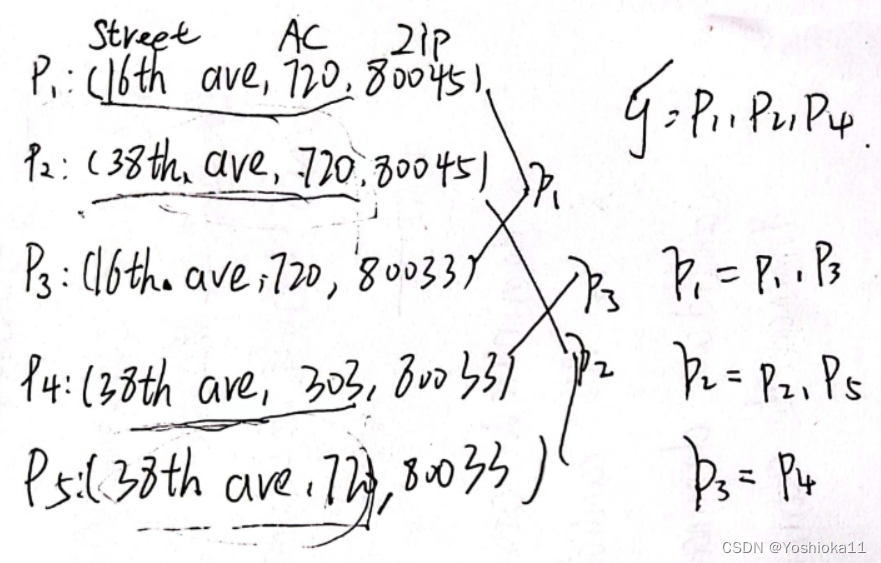
算法1：计算全局模式

        获得全局模式集。1、首先将每条元组左值相同的元组聚集到Px中。px是模式，只表示关键属性的值。2、计算每个模式的可信度c(x),后面看不懂了，原理图片放这先。

 算法2：源可信度计算

        该算法就是通过规则、数据源的可信度来进行恢复。伪代码如下：

        首先将全局模式规则GPS进行导入，遍历每个元组。如果某个元组的模式与各个规则中的不相同（注意：规则包含左部和右部，规则可以看作是条件函数依赖），有不一样的就认为元组有问题。计算各个数据源的可靠性，将最可靠（应该也有开销最小）的值赋给要修复的元组。

 3、数据源可靠性的定义：

       如果元组不符合规则，则可以说明该元组可能存在着错误。数据源的可靠性通过其他源来确定。公式如下：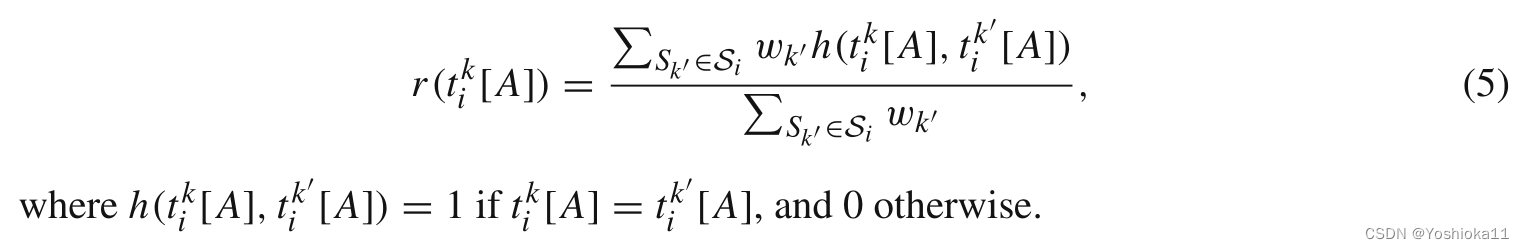

含义就是通过比对同一属性不同数据源的属性值，每比对一个元素值，如果元素值一样+1，元素值不一样+0，最后计算总比了值得元素数的占比。

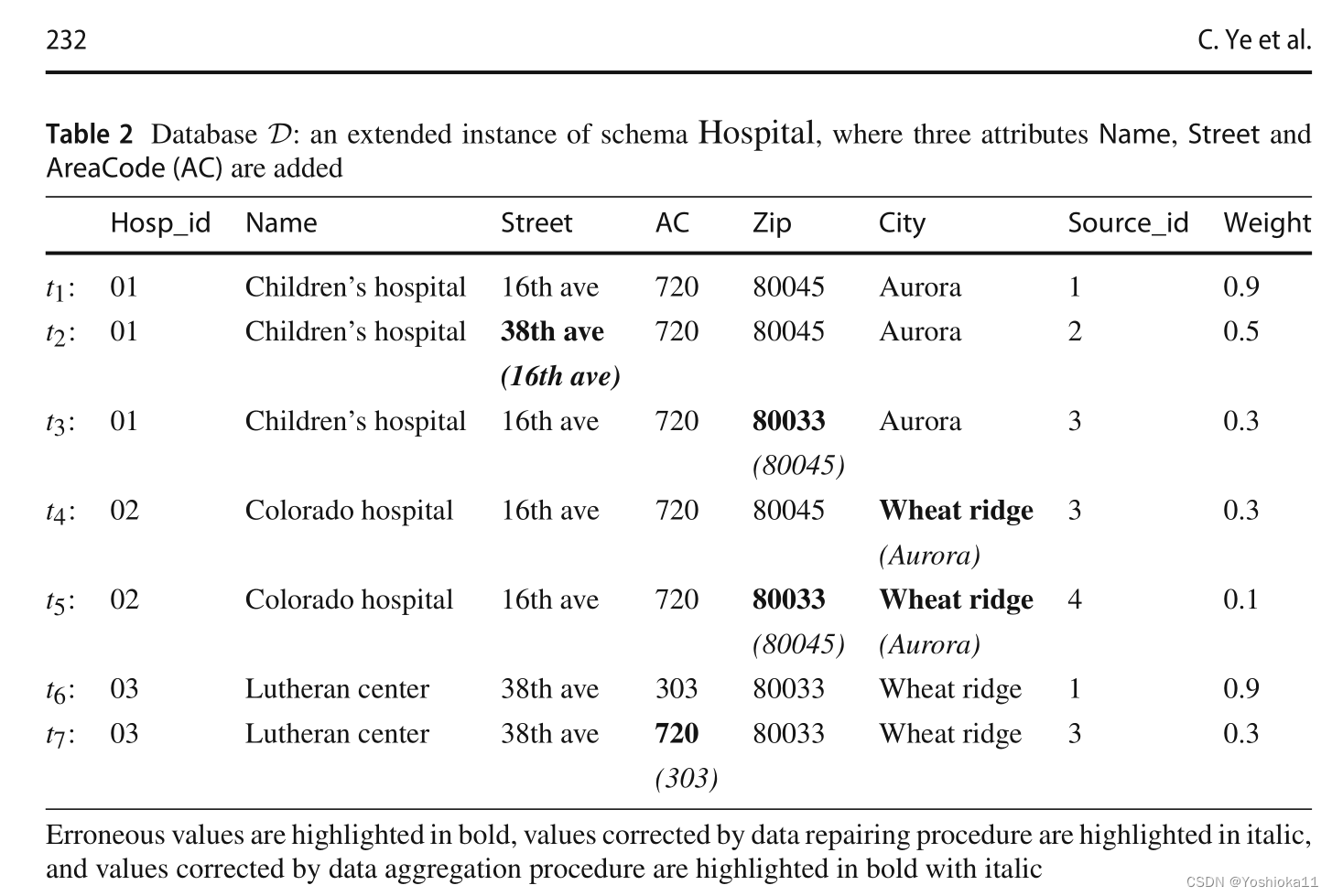
 已知元组7不满足全局模式，在修复前需要考虑对哪个属性值进行修复。Street or AC or Zip?通过可靠性计算公式分别计算各个属性的可靠性，对可靠性最高的属性进行修改。计算过程：

4、完整性修复存在的问题：

 前三个是全局模式，第四个与前三个不符，需要对P4进行修改。然而出现以下问题：若同时考虑对左部和右部都考虑进去，那么是将中间项改成Apt 11以满足P2，还是将14333改为14221以满足P3还是将Apt 11改为Apt 17以满足P2。李建中的方法时：只动右部，不动左部（Therefore,the repair may be unstable.This is the reason why we always choose the repair that modifies the dependent attribute Y）。

个人的问题：1、全局模式是怎么选出来的，是否一定要按照这个规则？2、P1，P2能算做是个冲突？
①为什么选择出来的全局模式规则会不包含一些元组的左部？筛选的规则是社么？
②不能当作是冲突，因为左部相同可以推出右部相同。但规则不包含“右部相同，左部也得相同”。

相互关联约束的修复框架

1、相互关联的约束：

右部都通过某一规则去修复某一元组，可能会导致修复后违反其他的规则。解决措施：按照一定的顺序进行修复。基础思想是为了保持数据的一致性，每一个属性值修改一次。

2、算法3：基于相关规则修复

        每当通过关联规则处理完成后，将属性F-Q放进属性Q中，以后将不再修改Q中的属性值。（为了保证修复之间不冲突，每个属性只能修复一次）

          建立一个空的Clean Attritbute Set，计算出相关规则的全局模式。遍历每个元组，判断元组是否满足全局模式。对不满足的元组,遍历F-Q中的属性，分别计算各个属性的可靠性。最后得到修改的数据集。
        该算法与算法2很像，不同之处在于只能修改可修改属性中的值（该方法是对可修改的属性作了限制）。在修复循环中完整成，修复的属性会将放到Clean 属性集中（line 13）。

        例子4.5

        假设有规则F1和F2，在最开始时通过F1进行修复，修复过程是上一个例子。当F1修复完后，将F1包含的所有属性放入到Clean 属性集中。在今后的修复中将不再考虑这些属性。在按照F2规则进行修复时，仅考虑City属性。

存在的问题   

        不同的orders导致修复的结果不同，因此需要找到一个合适的order策略。（没具体看）

 解决源间的冲突

        通过数据聚合检测多源间的冲突。

实验对比

1、涉及的算法

        基于规则的修复方法：Greedy,Sampling,LLUNATIC
        基于数据聚合的方法：CRH,Voting

2、涉及的数据集

6
https://opendata.cityofnewyork.us/.
7
https://www.yelp.com/nyc.
8
https://www.yellowpages.com/.
9
http://www.nychealthratings.com/.
10
http://test.supertour.com/newyork-ny.us.aspx.
11
https://tools.usps.com/go/ZipLookupAction.

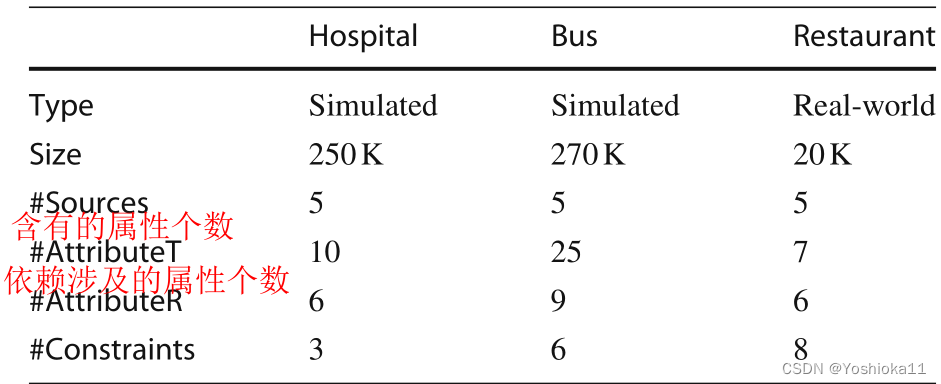
        Hospital有3个约束，[PN] → [AN],[ZC] → [CT],[MC] → [MN].
        Bus有4个约束，[LC] → [LN, PN],[PN] → [AC],[CT, MT] → [RN, MD, ST].

3、实验比对

        对数据集掺加噪声，使数据含有一些错误。通过掺加不同程度的噪声，对各个算法的精确度进行对比。最终的比对结果就是，自己提出的方法各方面吊打其他算法。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！