• 定义：找到一个函数 $function$ ，通过输入特征 $x$，输出一个数值 $Scalar$。

建模步骤

step1：模型假设，选择模型框架（线性模型）

一元线性模型（单个特征）

线性模型假设 y = b + w ⋅ x c p y = b + w·x_{cp} y=b+w⋅xcp​ （一元一次）

多元线性模型（多个特征）

y = b + ∑ w i x i y = b + \sum w_ix_i y=b+∑wi​xi​

• x i x_i xi​：就是各种特征(fetrure) x c p , x h p , x w , x h , ⋅ ⋅ ⋅ x_{cp},x_{hp},x_w,x_h,··· xcp​,xhp​,xw​,xh​,⋅⋅⋅
• w i w_i wi​：各个特征的权重 w c p , w h p , w w , w h , ⋅ ⋅ w_{cp},w_{hp},w_w,w_h,·· wcp​,whp​,ww​,wh​,⋅⋅
• $b$：偏移量

step2：模型评估，如何判断众多模型的好坏（损失函数）

以【单个特征】为例

• 使用距离，求【实际值】与【模型预测值】差，来判定模型的好坏。即使用损失函数（Loss function） 来衡量模型的好坏。统计若干（例中为10）组原始数据 ( y ^ n − f ( x c p n ) ) 2 \left ( \hat{y}^n - f(x_{cp}^n) \right )^2 (y^​n−f(xcpn​))2 的和，和越小模型越好。
• 损失函数 Loss function： L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=∑n=110​(y^​n−(b+w⋅xcp​))2

step3：模型优化，如何筛选最优的模型（梯度下降）

以【单个特征】为例
已知损失函数是 L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=∑n=110​(y^​n−(b+w⋅xcp​))2 ，需要找到一个令结果最小的 f ∗ f^* f∗

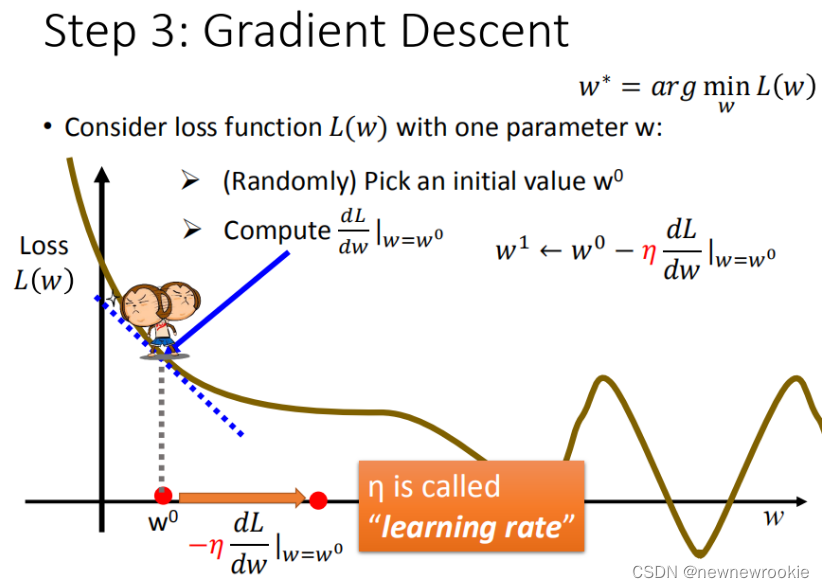
学习率 ：移动的步长，如图中 $\eta$

• 步骤1：随机选取一个 w 0 w^0 w0
• 步骤2：计算微分，也就是当前的斜率，根据斜率来判定移动的方向
  • 大于0向右移动（增加$w$）
  • 小于0向左移动（减少$w$）
• 步骤3：根据学习率移动
• 重复步骤2和步骤3，直到找到最低点（但此时有可能会找到局部最小值，而非全局最小值）

对于b同样进行上述步骤

梯度下降的问题：

• 问题1：当前最优（Stuck at local minima）
• 问题2：等于0（Stuck at saddle point）
• 问题3：趋近于0（Very slow at the plateau）

过拟合问题：在训练集上面表现优秀的模型，在测试集上效果不佳。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！