线性回归实例——牙膏的销售量(Python实现、OLS最小二乘)
线性回归实例——牙膏的销售量(Python、OLS最小二乘)
一、问题:
建立牙膏销售量与价格、广告投入之间的模型,预测在不同价格和广告费用下的牙膏销售量。下列数据收集了30个销售周期本公司牙膏销售量、价格、广告费用及同期其他厂家同类牙膏的平均售价。
| 销售周期 | 公司销售价格 | 其它厂家平均价格 | 广告费用 | 价格差 | 销售量 |
|---|---|---|---|---|---|
| 1 | 3.85 | 3.8 | 5.5 | -0.05 | 7.38 |
| 2 | 3.75 | 4 | 6.75 | 0.25 | 8.51 |
| 3 | 3.7 | 4.3 | 7.25 | 0.6 | 9.52 |
| 4 | 3.7 | 3.7 | 5.5 | 0 | 7.5 |
| 5 | 3.6 | 3.85 | 7 | 0.25 | 9.33 |
| 6 | 3.6 | 3.8 | 6.5 | 0.2 | 8.28 |
| 7 | 3.6 | 3.75 | 6.75 | 0.15 | 8.75 |
| 8 | 3.8 | 3.85 | 5.25 | 0.05 | 7.87 |
| 9 | 3.8 | 3.65 | 5.25 | -0.15 | 7.1 |
| 10 | 3.85 | 4 | 6 | 0.15 | 8 |
| 11 | 3.9 | 4.1 | 6.5 | 0.2 | 7.89 |
| 12 | 3.7 | 3.8 | 6.25 | 0.1 | 8.15 |
| 13 | 3.75 | 4.15 | 7 | 0.4 | 9.1 |
| 14 | 3.75 | 4.2 | 6.9 | 0.45 | 8.86 |
| 15 | 3.8 | 4.15 | 6.8 | 0.35 | 8.9 |
| 16 | 3.7 | 4 | 6.8 | 0.3 | 8.87 |
| 17 | 3.8 | 4.3 | 7.1 | 0.5 | 9.26 |
| 18 | 3.8 | 4.3 | 7 | 0.5 | 9 |
| 19 | 3.7 | 4.1 | 6.8 | 0.4 | 8.75 |
| 20 | 3.8 | 3.75 | 6.5 | -0.05 | 7.95 |
| 21 | 3.8 | 3.75 | 6.25 | -0.05 | 7.65 |
| 22 | 3.75 | 3.65 | 6 | -0.1 | 7.27 |
| 23 | 3.7 | 3.9 | 6.5 | 0.2 | 8 |
| 24 | 3.55 | 3.65 | 7 | 0.1 | 8.5 |
| 25 | 3.6 | 4.1 | 6.8 | 0.5 | 8.75 |
| 26 | 3.65 | 4.25 | 6.8 | 0.6 | 9.21 |
| 27 | 3.7 | 3.65 | 6.5 | -0.05 | 8.27 |
| 28 | 3.75 | 3.75 | 5.75 | 0 | 7.67 |
| 29 | 3.8 | 3.85 | 5.8 | 0.05 | 7.93 |
| 30 | 3.7 | 4.25 | 6.8 | 0.55 | 9.26 |
二、分析与假设:
由于牙膏是生活必需品,对大多数顾客来说,在购买同类产品时更多的会在意不同品牌之间的价格差异,而不是它们本身的价格。因此,在研究各个因素对销售量的影响时,用价格差代替公司销售价格和其他厂家平均价格更为合适。
三、基本模型:
变量解释:
y y y~公司牙膏销售量
x 1 x_{1} x1~其他厂家与本公司价格差
x 2 x_{2} x2~公司广告费用
下图为变量 y y y与 x 1 x_{1} x1的散点图(图中蓝色区域为置信带)。

可以看出, y y y与 x 1 x_{1} x1之间存在 y = β 0 + β 1 x 1 + ϵ y = \beta_{0}+\beta_{1}x_{1}+\epsilon y=β0+β1x1+ϵ 的线性关系,拟合直线为 y 1 = 7.814 + 2.665 y_{1} = 7.814+2.665 y1=7.814+2.665 × \times × x 1 x_{1} x1。
下图为 y y y与 x 2 x_{2} x2的散点图。
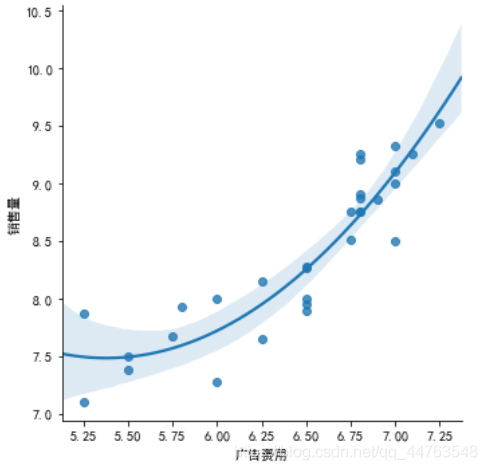
可以看出, y y y与 x 2 x_{2} x2之间存在 y = β 0 ′ + β 1 ′ x 2 + β 2 x 2 2 + ϵ ′ y = \beta_{0}'+\beta_{1}'x_{2}+\beta_{2}x_2^2+\epsilon' y=β0′+β1′x2+β2x22+ϵ′ 的线性关系,拟合曲线为 y 2 = 25.109 − 6.559 y_{2} = 25.109-6.559 y2=25.109−6.559 × \times × x 2 + 25.109 x_{2}+25.109 x2+25.109 × \times × x 2 2 x_2^2 x22。
根据 y y y分别与 x 1 x_{1} x1和 x 2 x_{2} x2的关系可以建立如下模型:
y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 2 2 + ϵ y = \beta_{0}+\beta_{1}x_{1}+\beta_{2}x_2+\beta_{3}x_2^2+\epsilon y=β0+β1x1+β2x2+β3x22+ϵ
四、模型求解及全部代码展示:
第一步,导入部分库以及解决画图时中文格式不兼容的问题(最后三行代码)。
#导入库
from __future__ import print_function #是为了在老版本的python中兼顾新特性的一种方法
import numpy as np #由多维数组对象和用于处理数组的例程集合组成的库
import pandas as pd #用于数据导入及整理的模块
import seaborn as sns
import statsmodels.api as sm #用于拟合多种统计模型,执行统计测试以及数据探索和可视化
import matplotlib.pyplot as plt
from sklearn import model_selection #对机器学习的方法进行了封装
from sklearn.linear_model import LinearRegression
from statsmodels.sandbox.regression.predstd import wls_prediction_std #返回拟合模型数据的标准偏差和置信区间
import matplotlib as mpl
from matplotlib.pyplot import savefig
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
第二步,导入数据和变量描述。
#导入数据
yagao = pd.read_csv("yagao.csv",usecols = [3,4,5]) #此处yayao数据为本文开头给定的表格数据#变量描述
y = yagao['销售量']
x1 = yagao['价格差']
x2 = yagao['广告费用']
x3 = x2**2
x4 = x1*x2
第三步,分析 y y y(销售量) 和 x 1 x_{1} x1(价格差) 之间的关系,通过画图得以直观表达。
#y = b0 + b1x1 + e
sns.lmplot(x = '价格差',y = '销售量',data=yagao,order=1)
plt.show()

求解拟合直线 y 1 y_{1} y1。
#拟合线y1求解
x1_1 = yagao['价格差']
parameter_y1 = np.polyfit(x1_1, y, 1)
line = 'y1直线为:' + '\ty1' + ' = ' + str(parameter_y1[1]) + ' + ' + str(parameter_y1[0]) + '*x1 '
print(line)
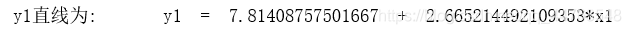
分析 y y y(销售量) 和 x 2 x_{2} x2(广告费用) 之间的关系,通过画图得以直观表达。
#y = b0 + b1x2 + b2x2**2 + e
sns.lmplot(x = '广告费用',y = '销售量',data=yagao,order=2)
plt.show()

#拟合曲线y2求解
parameter_y2 = np.polyfit(x2, y, 2)
curve = 'y2二次曲线为:' + '\ty2' + ' = ' + str(parameter_y2[2]) + ' + ' + str(parameter_y2[1]) + '*x2 ' + '+ ' + str(parameter_y2[2]) + '*x2**2'
print(curve)
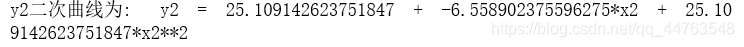
第四步(最重要一步),求解模型回归系数: β 0 、 β 1 、 β 2 、 β 3 \beta_{0}、\beta_{1}、\beta_{2}、\beta_{3} β0、β1、β2、β3
本文用OLS普通最小二乘法求解,在下列代码(‘y ~ x1 + x2 + x3’, data = yagao)中,y表示因变量。有几个变量则在y ~后边就表示成变量相加的格式,模型会自动求解出变量前的回归系数。
#y = b0 + b1x1 + b2x2 + b3x2**2 + e
model_1 = sm.formula.ols('y ~ x1 + x2 + x3', data = yagao).fit() #OLS普通最小二乘法
model_1.summary()
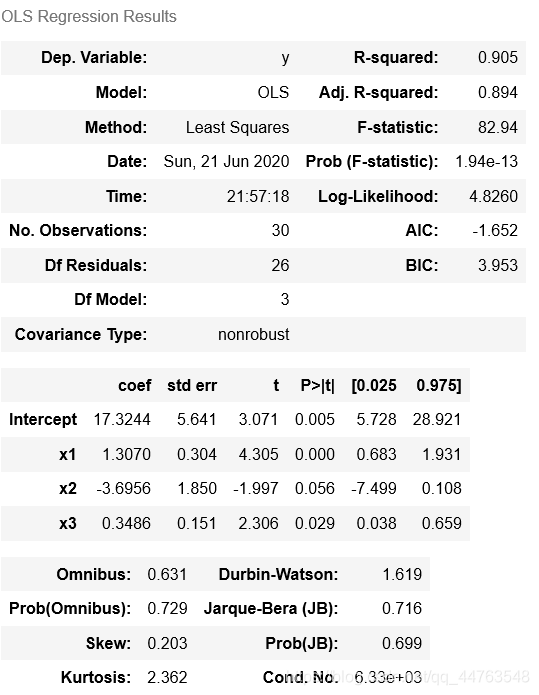
下面是模型结果中部分参数的解释。
左边:
Dep.Variable: 输出变量的名称
Model: 模型名称
Method: 方法,其中 Least Squares 表示最小二乘法
Date: 日期
Time: 时间
No.Observations: 样本数目
Df Residuals: 残差自由度
Df Model: 模型参数个数,相当于输入的X的元素个数
右边:
R- squared: 可决系数,用来判断估计的准确性,范围在[0,1]越接近1,说明对y的解释能力越强,拟合越好
Adj-R- squared: 通过样本数量与模型数量对R-squared进行修正,奥卡姆剃刀原理,避免描述冗杂
F-statistic: 衡量拟合的显著性,重要程度
Prob(F-statistic): 当prob(F-statistic)<α时,表示拒绝原假设,即认为模型是显著的
Log likelihood: 对数似然比LLR
AIC: 衡量拟合优良性
BIC: 贝叶斯信息准则
主要看此处的结果。Intercept表示 β 0 \beta_{0} β0 的数值, x 1 、 x 2 、 x 3 x_{1}、x_{2}、x_{3} x1、x2、x3分别表示求得自身系数 β 1 、 β 2 、 β 3 \beta_{1}、\beta_{2}、\beta_{3} β1、β2、β3 的数值。
coef: 系数
std err: 系数估计的基本标准误差
t: t统计值,衡量系数统计显著程度的指标
P>|t|: P值
[0.025,0.975]: 95%置信区间的下限和上限值
五、模型结果分析:
综上所得, R 2 = 0.905 , F = 82.94 , p 约 为 0 R^2=0.905,F=82.94,p约为0 R2=0.905,F=82.94,p约为0。 y y y的 90.54 90.54 90.54%可由模型确定,且 p p p远小于 α = 0.05 \alpha=0.05 α=0.05, F F F远超过 F F F检验的临界值(2.975),模型从整体上看成立。需要注意 β 2 \beta_{2} β2的置信区间包含零点 ,按道理应该将 x 2 x_{2} x2去掉,不过其置信区间右端点距离零点很近,又因为 x 2 2 x_{2}^2 x22项显著,所以仍可将 x 2 x_{2} x2保留在模型中。
六、模型改进:
x 1 x_{1} x1和 x 2 x_{2} x2对y的影响独立,可以推断出 x 1 x_{1} x1和 x 2 x_{2} x2对 y y y的影响又交互作用(什么为交互作用?举个例子,假如你在商店买牙膏,货架上的牙膏琳琅满目,不同品牌牙膏售价不同视作价格差。每种牙膏的知名度是不同的,比如某种牙膏在电视上做的广告多所以知名度高,视作广告费用高。交互作用的意思是,牙膏A的价格比其它同类牙膏的价格贵一些,即价格差大,但是因为牙膏A的知名度高,所以你可能不那么在意价格差大的影响而因为知名度的原因继续购买牙膏A,这就叫做交互影响。反之,虽然牙膏B的知名度高,花在广告上的钱很多,但是因为牙膏B太贵了所以你放弃买牙膏B。)
综上可以考虑加入交互项 x 1 x 2 x_{1}x_{2} x1x2,记作 x 4 x_{4} x4。
七、新模型求解与比较:
model_2 = sm.formula.ols('y ~ x1 + x2 + x3 + x4', data = yagao).fit()
model_2.summary()
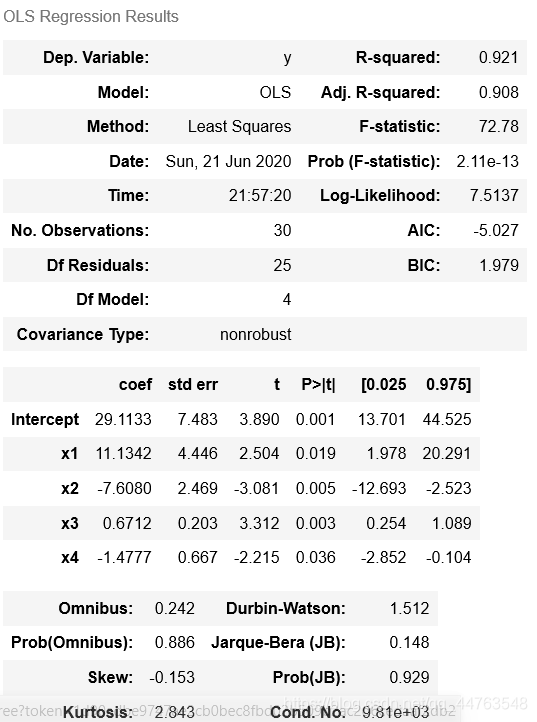
求得, R 2 = 0.921 , F = 77.78 , p 约 为 0 R^2=0.921,F=77.78,p约为0 R2=0.921,F=77.78,p约为0,模型良好且参数估计值的置信区间都不包含零点。
八、总结:
至于对两模型销售量预测比较等操作过于简单不予展示。
从这个实例我们可以看到,建立回归模型可以先根据已知的数据,从常识和经验进行分析,做出散点图,决定取哪几个回归变量,及它们的函数形式。用软件求解后作统计分析,每个回归系数置信区间是否包含零点,可以用来检验对应的回归变量对因变量的影响是否显著(若包含零点则不显著)。如果对模型不够满意,则应改进模型,如添加二次项、交互项等。
对因变量进行预测,经常是建立回归模型的主要目的之一。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!