机器学习技法 之 矩阵分解（Matrix Factorization）

线性神经网络（Linear Network Hypothesis）

这里用推荐系统的应用实例引出矩阵分解：

现在有一个电影评分预测问题，那么数据集的组成为：

{ ( x ~ n = ( n ) , y n = r n m ) : user  n rated movie  m } \left\{ \left( \tilde { \mathbf { x } } _ { n } = ( n ) , y _ { n } = r _ { n m } \right) : \text { user } n \text { rated movie } m \right\} {(x~n​=(n),yn​=rnm​): user n rated movie m}

其中 x ~ n = ( n ) \tilde { \mathbf { x } } _ { n } = (n) x~n​=(n) 是一种抽象的类别（categorical）特征。

什么是类别特征呢？举例来说：比如ID号，血型（A，B，AB，O），编程语言种类（C++，Python，Java）。

但是大部分机器学习算法都是基于数值型特征实现的，当然决策树除外。所以现在需要将类别特征转换（编码，encoding）为数值特征。这里需要转换的特征是ID号。使用的工具是二值向量编码（binary vector encoding），也就是向量的每个元素只有两种数值选择，这里选择的是 0/1 向量编码，对应关系是向量中的第 ID 个元素为 1，其他元素均为 0。

那么第 m 个电影编码后的数据集 D m \mathcal D_m Dm​ 可以表示为:

{ ( x n = Binary VectorEncoding  ( n ) , y n = r n m ) : user  n rated movie  m } \left\{ \left( \mathbf { x } _ { n } = \text { Binary VectorEncoding } ( n ) , y _ { n } = r _ { n m } \right) : \text { user } n \text { rated movie } m \right\} {(xn​= Binary VectorEncoding (n),yn​=rnm​): user n rated movie m}

如果将全部的电影数据整合到一起的数据集 $\mathcal{D}$ 可以表示为：

{ ( x n = Binary VectorEncoding  ( n ) , y n = [ r n 1 ? ? r n 4 r n 5 … r n M ] T ) } \left\{ \left( \mathbf { x } _ { n } = \text { Binary VectorEncoding } ( n ) , \mathbf { y } _ { n } = \left[ \begin{array} { l l l l l l } r _ { n 1 } & ? & ? & r _ { n 4 } & r _ { n 5 } & \ldots & r _ { n M } \end{array} \right] ^ { T } \right) \right\} {(xn​= Binary VectorEncoding (n),yn​=[rn1​​?​?​rn4​​rn5​​…​rnM​​]T)}

其中 $?$ 代表了该电影未评分。

现在的想法是使用一个 N − d ~ − M N - \tilde { d } - M N−d~−M 神经网络进行特征提取：

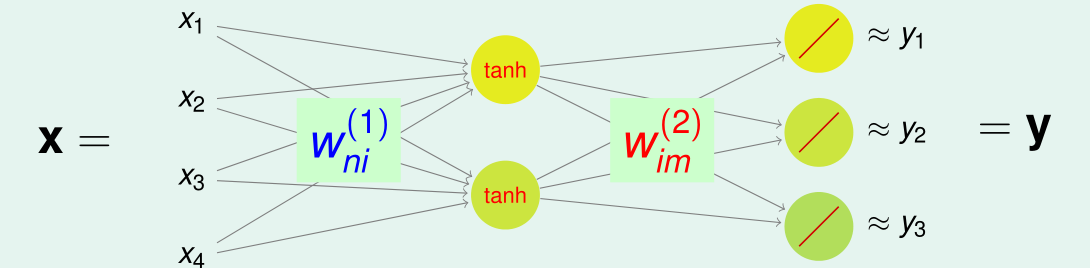
现在先使用线性的激活函数，那么由此得到的线性神经网络的结构示意图为：

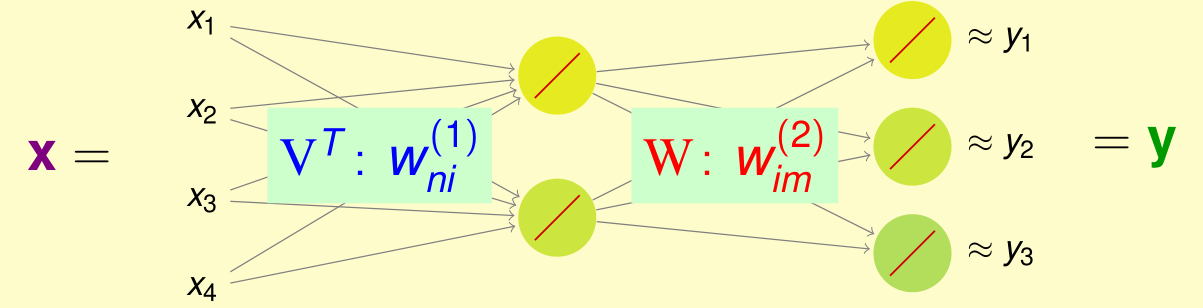
基本矩阵分解（Basic Matrix Factorization）

那么现在将权重矩阵进行重命名：

V T for  [ w n i ( 1 ) ] and  W for  [ w i m ( 2 ) ] \mathrm { V } ^ { T } \text { for } \left[ w _ { n i } ^ { ( 1 ) } \right] \text { and } \mathrm { W } \text { for } \left[ w _ { i m } ^ { ( 2 ) } \right] VT for [wni(1)​] and W for [wim(2)​]

那么假设函数可以写为：

h ( x ) = W T V x ⏟ Φ ( x ) \mathrm { h } ( \mathrm { x } ) = \mathrm { W } ^ { T } \underbrace { \mathrm { Vx } } _ { \Phi ( \mathrm { x } ) } h(x)=WTΦ(x) Vx​​

矩阵 $\mathrm{V}$ 实际上就是特征转换 $\Phi (\mathrm{x})$，然后再使用 $\mathrm{W}$ 进行实现一个基于转换数据的线性模型。那么根据 ID 的数值编码规则，第 $n$ 个用户的假设函数可以写为：

h ( x n ) = W T v n , where  v n is  n -th column of  V \mathrm { h } \left( \mathrm { x } _ { n } \right) = \mathrm { W } ^ { T } \mathbf { v } _ { n } , \text { where } \mathbf { v } _ { n } \text { is } n \text { -th column of } \mathrm { V } h(xn​)=WTvn​, where vn​ is n -th column of V

第 $m$ 个电影的假设函数可以写为：

h m ( x ) = w m T Φ ( x ) h _ { m } ( \mathbf { x } ) = \mathbf { w } _ { m } ^ { T } \mathbf { \Phi } ( \mathbf { x } ) hm​(x)=wmT​Φ(x)

那么对于推荐系统来说现在需要进行 $\mathrm{W}$ 和 $\mathrm{V}$ 的最优解求取。

对于$\mathrm{W}$ 和 $\mathrm{V}$ 来说理想状态是：

r n m = y n ≈ w m T v n = v n T w m ⟺ R ≈ V T W r _ { n m } = y _ { n } \approx \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n }= \mathbf { v } _ { n } ^ { T } \mathbf { w } _ { m } \Longleftrightarrow \mathbf { R } \approx \mathbf { V } ^ { T } \mathbf { W } rnm​=yn​≈wmT​vn​=vnT​wm​⟺R≈VTW

也就是说特征转换矩阵 $\mathbf{V}$ 和线性模型矩阵 $\mathbf{W}$ 相乘的结果是评分矩阵。

还记得在机器学习基石中的评分预测示意图吗？观看者和电影都有自己的特征向量，只需要计算两个向量的相似度便可以用了预测评分。观看者和电影向量在这里指的是 v n \mathbf { v } _ { n } vn​ 和 w m \mathbf { w } _ { m } wm​。

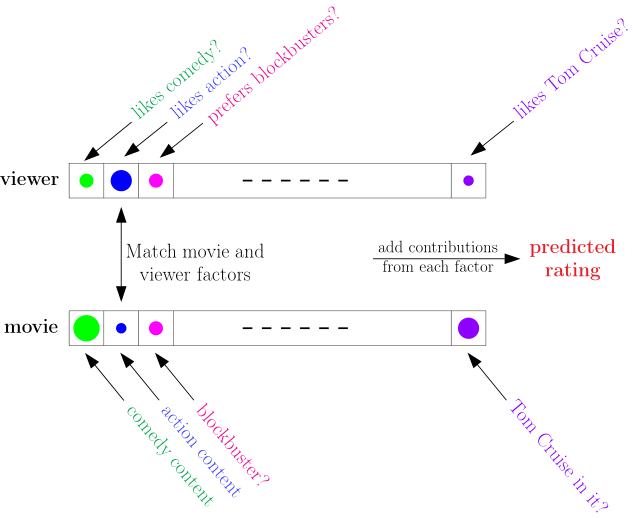
那么对于数据集 $\mathcal{D}$ ，该假设函数的基于平方误差的误差测量为：

E i n ( { w m } , { v n } ) = 1 ∑ m = 1 M ∣ D m ∣ ∑ user  n rated movie  m ( r n m − w m T v n ) 2 E _ { \mathrm { in } } \left( \left\{ \mathbf { w } _ { m } \right\} , \left\{ \mathbf { v } _ { n } \right\} \right) = \frac { 1 } { \sum _ { m = 1 } ^ { M } \left| \mathcal { D } _ { m } \right| } \sum _ { \text {user } n \text { rated movie } m } \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) ^ { 2 } Ein​({wm​},{vn​})=∑m=1M​∣Dm​∣1​user n rated movie m∑​(rnm​−wmT​vn​)2

那么现在就要根据数据集 $\mathcal{D}$ 进行 v n \mathbf { v } _ { n } vn​ 和 w m \mathbf { w } _ { m } wm​ 的学习来保证误差最小。

min ⁡ W , V E i n ( { w m } , { v n } ) ∝ ∑ u s e r n rated movie  m ( r n m − w m T v n ) 2 = ∑ m = 1 M ( ∑ ( x n , r n m ) ∈ D m ( r n m − w m T v n ) 2 ) ( 1 ) = ∑ n = 1 N ( ∑ ( x n , r n m ) ∈ D m ( r n m − v n T w m ) 2 ) ( 2 ) \begin{aligned} \min _ { \mathrm { W } , \mathrm { V } } E _ { \mathrm { in } } \left( \left\{ \mathbf { w } _ { m } \right\} , \left\{ \mathbf { v } _ { n } \right\} \right) & \propto \sum _ { \mathrm { user } n \text { rated movie } m } \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) ^ { 2 } \\ & = \sum _ { m = 1 } ^ { M } \left( \sum _ { \left( \mathbf { x } _ { n } , r _ { n m } \right) \in \mathcal { D } _ { m } } \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) ^ { 2 } \right) (1)\\ & = \sum _ { n = 1 } ^ { N } \left( \sum _ { \left( \mathbf { x } _ { n } , r _ { n m } \right) \in \mathcal { D } _ { m } } \left( r _ { n m } - \mathbf { v } _ { n } ^ { T } \mathbf { w } _ { m } \right) ^ { 2 } \right) (2) \end{aligned} W,Vmin​Ein​({wm​},{vn​})​∝usern rated movie m∑​(rnm​−wmT​vn​)2=m=1∑M​⎝⎛​(xn​,rnm​)∈Dm​∑​(rnm​−wmT​vn​)2⎠⎞​(1)=n=1∑N​⎝⎛​(xn​,rnm​)∈Dm​∑​(rnm​−vnT​wm​)2⎠⎞​(2)​

由于上式中有 v n \mathbf { v } _ { n } vn​ 和 w m \mathbf { w } _ { m } wm​ 两个变量，同时优化的话可能会很困难，所以基本的想法是使用交替最小化操作（alternating minimization）：

1. 固定 v n \mathbf { v } _ { n } vn​，也就是说固定用户特征向量，然后求取每一个 w m ≡ minimize  E in  within  D m \mathbf { w } _ { m } \equiv \text { minimize } E _ { \text {in } } \text { within } \mathcal { D } _ { m } wm​≡ minimize Ein ​ within Dm​。
2. 固定 w m \mathbf { w } _ { m } wm​，也就是说电影的特征向量，然后求取每一个 v n ≡ minimize  E in  within  D m \mathbf { v } _ { n } \equiv \text { minimize } E _ { \text {in } } \text { within } \mathcal { D } _ { m } vn​≡ minimize Ein ​ within Dm​。

这一过程叫做交替最小二乘算法（alternating least squares algorithm）。该算法的具体实现如下：

initialize  d ~ dimension vectors  { w m } , { v n } alternating optimization of  E in  : repeatedly  optimize  w 1 , w 2 , … , w M :  update  w m by  m -th-movie linear regression on  { ( v n , r n m ) } optimize  v 1 , v 2 , … , v N :  update  v n by  n -th-user linear regression on  { ( w m , r n m ) } until converge  \begin{array} { l } \text { initialize } \tilde { d } \text { dimension vectors } \left\{ \mathbf { w } _ { m } \right\} , \left\{ \mathbf { v } _ { n } \right\} \\ \text { alternating optimization of } E _ { \text {in } } : \text { repeatedly } \\ \qquad \text { optimize } \mathbf { w } _ { 1 } , \mathbf { w } _ { 2 } , \ldots , \mathbf { w } _ { M } \text { : } \text { update } \mathbf { w } _ { m } \text { by } m \text { -th-movie linear regression on } \left\{ \left( \mathbf { v } _ { n } , r _ { n m } \right) \right\} \\ \qquad \text { optimize } \mathbf { v } _ { 1 } , \mathbf { v } _ { 2 } , \ldots , \mathbf { v } _ { N } \text { : } \text { update } \mathbf { v } _ { n } \text { by } n \text { -th-user linear regression on } \left\{ \left( \mathbf { w } _ { m } , r _ { n m } \right) \right\} \\ \text { until converge } \end{array}  initialize d~ dimension vectors {wm​},{vn​} alternating optimization of Ein ​: repeatedly  optimize w1​,w2​,…,wM​ :  update wm​ by m -th-movie linear regression on {(vn​,rnm​)} optimize v1​,v2​,…,vN​ :  update vn​ by n -th-user linear regression on {(wm​,rnm​)} until converge ​

初始化过程使用的是随机（randomly）选取。随着迭代的过程保证了 E in  E _ { \text {in } } Ein ​ 不断下降，由此保证了收敛性。交替最小二乘的过程更像用户和电影在跳探戈舞。

线性自编码器与矩阵分解（Linear Autoencoder versus Matrix Factorization）

Linear Autoencoder Matrix Factorization goal X ≈ W ( W T X ) R ≈ V T W motivation special  d − d ~ − d linear NNet  N − d ~ − M linear NNet  solution global optimal at eigenvectors of  X T X local optimal via alternating least squares  usefulness extract dimension-reduced features  extract hidden user/movie features  \begin{array}{c|c|c} &\text{Linear Autoencoder}&\text{Matrix Factorization}\\ \hline \text{goal} &\mathrm { X } \approx \mathrm { W } \left( \mathrm { W } ^ { T } \mathrm { X } \right)&\mathbf { R } \approx \mathbf { V } ^ { T } \mathbf { W }\\ \hline \text{motivation}&\text { special } d - \tilde { d } - d \text { linear NNet }&N - \tilde { d } - M \text { linear NNet }\\ \hline \text{solution} &\text { global optimal at eigenvectors of } X ^ { T } X & \text {local optimal via alternating least squares } \\ \hline \text { usefulness} & \text { extract dimension-reduced features } & \text { extract hidden user/movie features } \end{array} goalmotivationsolution usefulness​Linear AutoencoderX≈W(WTX) special d−d~−d linear NNet  global optimal at eigenvectors of XTX extract dimension-reduced features ​Matrix FactorizationR≈VTWN−d~−M linear NNet local optimal via alternating least squares  extract hidden user/movie features ​​

所以线性自编码器是一种在矩阵 $\mathrm{X}$ 做的特殊的矩阵分解。

随机梯度法（Stochastic Gradient Descent）

相比交替迭代优化，另一种优化思路是随机梯度下降法。

回顾一下矩阵分解的误差测量函数：

E i n ( { w m } , { v n } ) ∝ ∑ user  n rated movie  m ( r n m − w m T v n ) 2 ⏟ err(user  n , movie  m , rating  r n m ) E _ { \mathrm { in } } \left( \left\{ \mathbf { w } _ { m } \right\} , \left\{ \mathbf { v } _ { n } \right\} \right) \propto \sum _ { \text {user } n \text { rated movie } m } \underbrace { \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) ^ { 2 } } _ { \text {err(user } n , \text { movie } m , \text { rating } r_{nm} )} Ein​({wm​},{vn​})∝user n rated movie m∑​err(user n, movie m, rating rnm​) (rnm​−wmT​vn​)2​​

随机梯度下降法高效且简单，可以拓展于其他的误差测量。

由于每次只是拿出一个样本进行优化，那么先观察一下单样本的误差测量：

err ⁡ ( user  n , movie  m , rating  r n m ) = ( r n m − w m T v n ) 2 \operatorname { err } \left( \text {user } n , \text { movie } m , \text { rating } r _ { n m } \right) = \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) ^ { 2 } err(user n, movie m, rating rnm​)=(rnm​−wmT​vn​)2

那么偏导数为：

∇ v n err ⁡ ( user  n , movie  m , rating  r n m ) = − 2 ( r n m − w m T v n ) w m ∇ w m err ⁡ ( user  n , movie  m , rating  r n m ) = − 2 ( r n m − w m T v n ) v n \begin{array} { r l } \nabla _ { \mathbf { v } _ { n } } & \operatorname { err } \left( \text { user } n , \text { movie } m , \text { rating } r _ { n m } \right) = - 2 \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) \mathbf { w } _ { m } \\ \nabla _ { \mathbf { w } _ { m } } & \operatorname { err } \left( \text { user } n , \text { movie } m , \text { rating } r _ { n m } \right) = - 2 \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) \mathbf { v } _ { n } \end{array} ∇vn​​∇wm​​​err( user n, movie m, rating rnm​)=−2(rnm​−wmT​vn​)wm​err( user n, movie m, rating rnm​)=−2(rnm​−wmT​vn​)vn​​

也就是说只对当前样本的 v n \mathbf { v } _ { n } vn​ 和 w m \mathbf { w } _ { m } wm​ 有影响，而其他的参数的偏导均为零。总结来说就是：

$$\text{per-example gradient }\propto -(\text{ residual })(\text{ the other feature vector })$$

那么使用随机梯度下降法求解矩阵分解的实际步骤为：

initialize  d ~ dimension vectors  { w m } , { v n } randomly  for  t = 0 , 1 , … , T (1) randomly pick  ( n , m ) within all known  r n m (2) calculate residual  r ~ n m = ( r n m − w m T v n ) (3) SGD-update:  v n n e w ← v n o l d + η ⋅ r ~ n m w m o l d w m n e w ← w m o l d + η ⋅ r ~ n m v n o l d \begin{array} { l } \text { initialize } \tilde { d } \text { dimension vectors } \left\{ \mathbf { w } _ { m } \right\} , \left\{ \mathbf { v } _ { n } \right\} \text { randomly } \\ \text{ for } t = 0,1 , \ldots , T \\ \qquad \text { (1) randomly pick } ( n , m ) \text { within all known } r _ { n m } \\ \qquad \text { (2) calculate residual } \tilde { r } _ { n m } = \left( r _ { n m } - \mathbf { w } _ { m } ^ { T } \mathbf { v } _ { n } \right) \\ \qquad \text { (3) SGD-update: } \\ \qquad\qquad\qquad \begin{aligned} \mathbf { v } _ { n } ^ { n e w } & \leftarrow \mathbf { v } _ { n } ^ { o l d } + \eta \cdot \tilde { r } _ { n m } \mathbf { w } _ { m } ^ { o l d } \\ \mathbf { w } _ { m } ^ { n e w } & \leftarrow \mathbf { w } _ { m } ^ { o l d } + \eta \cdot \tilde { r } _ { n m } \mathbf { v } _ { n } ^ { o l d } \end{aligned} \end{array}  initialize d~ dimension vectors {wm​},{vn​} randomly  for t=0,1,…,T (1) randomly pick (n,m) within all known rnm​ (2) calculate residual r~nm​=(rnm​−wmT​vn​) (3) SGD-update: vnnew​wmnew​​←vnold​+η⋅r~nm​wmold​←wmold​+η⋅r~nm​vnold​​​

但是注意一点随机梯度下降法是针对随机选到的样本进行优化的，那么针对一些对时间比较敏感的数据分析任务，比如近期的数据更有效，那么随机梯度下降法的随机选取应该偏重于近期的数据样本，那么效果可能会好一些。如果你明白这一点，那么在实际运用中会更容易修改该算法。

提取模型总结（Map of Extraction Models）

提取模型：思路是将特征转换作为隐变量嵌入线性模型（或者其他基础模型）中。也就是说除了模型的学习，还需要从资料中学到怎么样作转换能够有效的表现资料。

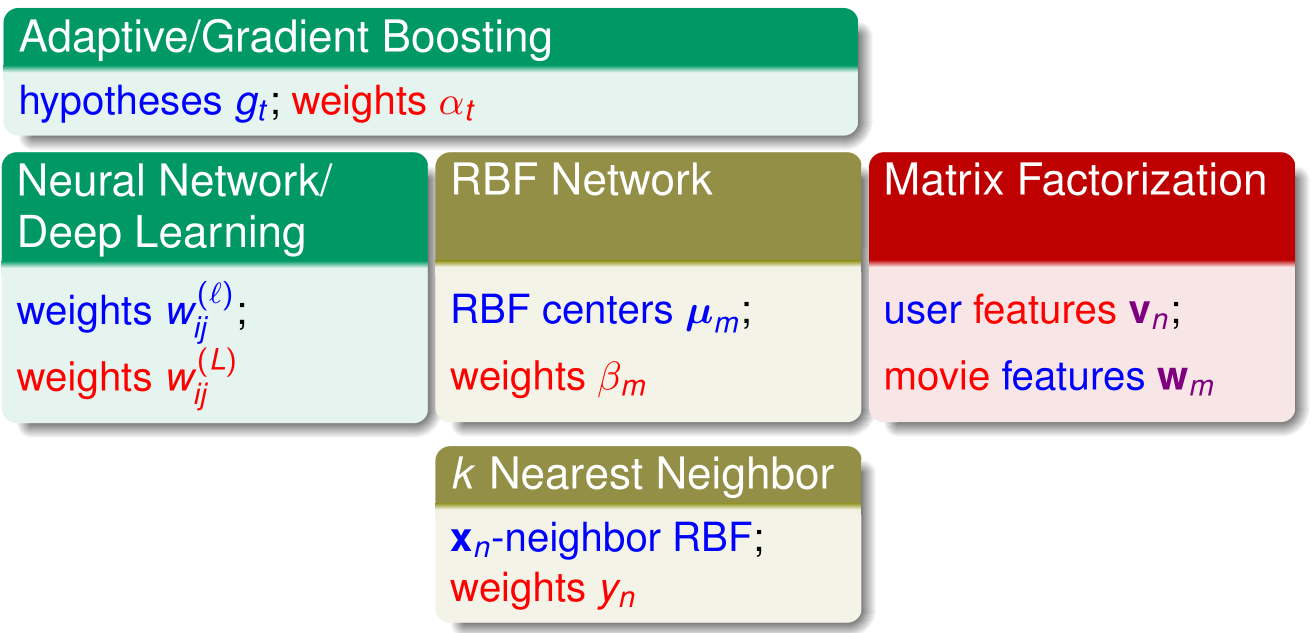
在神经网络或者深度学习中，隐含层的前 L - 1 层（ weights  w i j ( ℓ ) \text { weights } w _ { i j } ^ { ( \ell ) }  weights wij(ℓ)​）是进行特征的转换，最后一层是线性模型（ weights  w i j ( L ) \text { weights } w _ { i j } ^ { ( L ) }  weights wij(L)​）。也就是说在学习线性模型的同时，也学到了那些隐藏的转换。

在RBF网络中，最后一层也是线性模型（ weights  β m \text { weights } \beta _{ m }  weights βm​，而中间潜藏的变数（中心代表， RBF centers  μ m \text { RBF centers } \mu _ { m }  RBF centers μm​）也是一种特征的学习。

而在矩阵分解中，学习到了两个特征那就是 w m \mathbf { w } _ { m } wm​ 和 v n \mathbf { v } _ { n } vn​，两者可以叫线性模型的权重也可以叫特征向量，这是相对于用户还是电影，不同的对象功能不同。

而在 自适应提升和梯度提升（Adaptive/Gradient Boosting）中，实际上假设函数 g t g_t gt​ 的求解就是一种特征的学习，而所学习到的系数 α t \alpha_t αt​ 则是线性模型的权重系数。

相对来说在 k 邻近算法中，这 Top k 的邻居则是一种特征转换。而各个邻居投票系数 y n y_n yn​ 则是一种线性模型的权重系数。

提取技术总结（Map of Extraction Techniques）

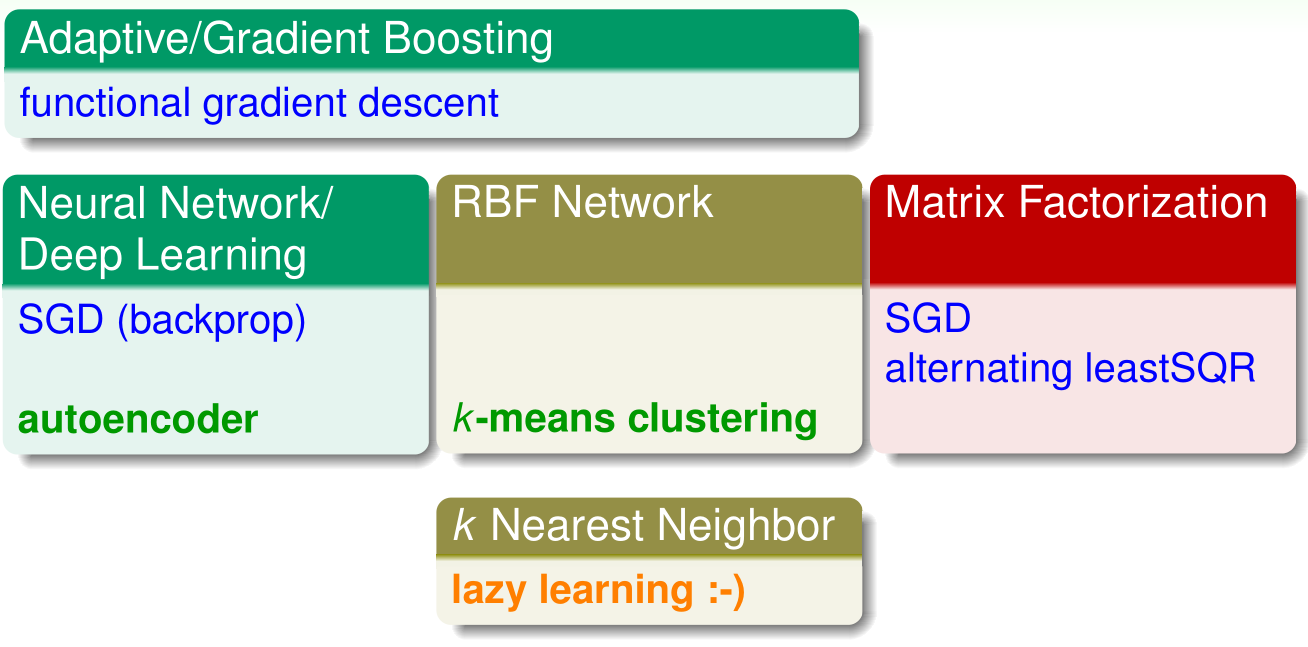
在神经网络或者深度学习中，则使用的是基于随机梯度下降法（SGD）的反向传播算法（backprop）。同时其中有一种特殊的实现：自编码器，将输入和输出保持一样，学习出一种压缩编码。

在RBF网络中，使用 k 均值聚类算法（k-means clustering）找出那些中心。

而在矩阵分解中，则可以使用的是 交替最小二乘（alternating leastSQR）和随机梯度下降（SGD）。

而在 自适应提升和梯度提升（Adaptive/Gradient Boosting）中，使用的技巧是梯度下降法（functional gradient descent）的思路还获取假设函数 g t g_t gt​ 的。

相对来说在 k 邻近算法中，则使用的是一种 lazy learning，什么意思呢？在训练过程中不做什么事情，而在测试过程中，拿已有的数据做一些推论。

提取模型的优缺（Pros and Cons of Extraction Models）

提取模型（Neural Network/Deep Learning、RBF Network 、Matrix Factorization）的优缺点如下：

优点：

• easy: reduces human burden in designing features
  简单：减小了设计特征的人力负担
• powerful : if enough hidden variables considered
  强有力：如果考虑足够多的隐变量的话

缺点

• hard: non-convex optimization problems in general
  困难：通常是非凸优化问题
• overfitting: needs proper regularization/validation
  过拟合：由于很有力，所以要合理使用正则化和验证工具

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！