拉格朗日对偶性

• 拉格朗日乘子法
• • 等式约束优化问题：
  • 不等式约束优化问题
• 原始问题
• 对偶问题
• 原始问题和对偶问题的关系（3个定理）
• • 定理C.1（ d ∗ d^* d∗和 p ∗ p^* p∗的关系）
  • 定理C.2（ d ∗ = p ∗ d^*=p^* d∗=p∗的条件）
  • 定理C.3（KKT条件）

拉格朗日乘子法

等式约束优化问题：

对于一个等式约束凸优化问题：
min ⁡ x ∈ R n f ( x ) \min_{x\in R^n}f(x) x∈Rnmin​f(x)
$$s.t.h(x)=0$$
x = ( x ( 1 ) , x ( 2 ) ) T x=(x^{(1)},x^{(2)})^T x=(x(1),x(2))T
f ( x ⃗ ) f(\vec{x}) f(x )为一个凸函数，如图：

便于进一步理解我们将其投影到 x ( 1 ) x^{(1)} x(1)- x ( 2 ) x^{(2)} x(2)的平面上：

只有当等高线和 h ( x ⃗ ) = 0 h(\vec{x})=0 h(x )=0 相切时，取得最优解 f ( x ⃗ ∗ ) f(\vec{x}^*) f(x ∗)，即梯度与等高线的法线是垂直的，两曲线的法向量平行，梯度是平行的：

∇ f ( x ⃗ ) ∥ ∇ h ( x ⃗ ) \nabla f(\vec{x})\parallel\nabla h(\vec{x}) ∇f(x )∥∇h(x )
即： ∂ f ∂ x ( 1 ) ∂ f ∂ x ( 2 ) = ∂ h ∂ x ( 1 ) ∂ h ∂ x ( 2 ) = − λ ( 梯 度 平 行 ， 且 方 向 是 相 反 的 , λ > 0 ) \frac { \frac{\partial f}{\partial x^{(1)}} } { \frac{\partial f}{\partial x^{(2)}} } = \frac { \frac{\partial h}{\partial x^{(1)}} } { \frac{\partial h}{\partial x^{(2)}} } = -\lambda(梯度平行，且方向是相反的,\lambda>0) ∂x(2)∂f​∂x(1)∂f​​=∂x(2)∂h​∂x(1)∂h​​=−λ(梯度平行，且方向是相反的,λ>0)
∂ f ∂ x ( 1 ) = λ ∂ h ∂ x ( 1 ) \frac{\partial f}{\partial x^{(1)}}=\lambda \frac{\partial h}{\partial x^{(1)}} ∂x(1)∂f​=λ∂x(1)∂h​
∂ f ∂ x ( 2 ) = λ ∂ h ∂ x ( 2 ) \frac{\partial f}{\partial x^{(2)}}=\lambda \frac{\partial h}{\partial x^{(2)}} ∂x(2)∂f​=λ∂x(2)∂h​
这样我们引入一个辅助函数： L ( x ⃗ , λ ) = f ( x ⃗ ) + λ h ( x ⃗ ) L(\vec{x},\lambda)=f(\vec{x})+\lambda h(\vec{x}) L(x ,λ)=f(x )+λh(x )
令
∂ L ∂ x ( 1 ) = ∂ f ∂ x ( 1 ) + λ ∂ h ∂ x ( 1 ) = 0 \frac{\partial L}{\partial x^{(1)}}=\frac{\partial f}{\partial x^{(1)}}+\lambda\frac{\partial h}{\partial x^{(1)}}=0 ∂x(1)∂L​=∂x(1)∂f​+λ∂x(1)∂h​=0
∂ L ∂ x ( 2 ) = ∂ f ∂ x ( 2 ) + λ ∂ h ∂ x ( 2 ) = 0 \frac{\partial L}{\partial x^{(2)}}=\frac{\partial f}{\partial x^{(2)}}+\lambda\frac{\partial h}{\partial x^{(2)}}=0 ∂x(2)∂L​=∂x(2)∂f​+λ∂x(2)∂h​=0
即：
∇ X L = ∂ L ∂ X = ∇ f + λ ∇ h = 0 \nabla_XL=\frac{\partial L}{\partial X}=\nabla f+\lambda\nabla h=0 ∇X​L=∂X∂L​=∇f+λ∇h=0
∇ λ L = ∂ L ∂ λ = h ( x ⃗ ) = 0 \nabla_\lambda L=\frac{\partial L}{\partial \lambda}=h(\vec{x})=0 ∇λ​L=∂λ∂L​=h(x )=0
这样两个方程联立求解的方法就叫做拉格朗日乘子法，$\lambda$就称为拉格朗日乘子。
得到我们的最优解 x ( 1 ) ∗ x^{(1)*} x(1)∗、 x ( 2 ) ∗ x^{(2)*} x(2)∗以及我们的目标函数的值 f ( x ⃗ ∗ ) f(\vec{x}^*) f(x ∗)

不等式约束优化问题

如果上述约束条件推广为不等式：
如，
min ⁡ x ∈ R n f ( x ) \min_{x\in R^n}f(x) x∈Rnmin​f(x)
$$s.t.h(x)\le 0$$
x = ( x ( 1 ) , x ( 2 ) ) T x=(x^{(1)},x^{(2)})^T x=(x(1),x(2))T

约束不等式 $h(x)\le 0$ 称为原始可行性（Primal Feasibility）。
我们分成 $h(x)<0$ 和 $h(x)=0$ 两种情况讨论：

（1）如果目标函数 f ( x ⃗ ) f(\vec{x}) f(x )在无约束下的极小值点在约束函数 h ( x ⃗ ) ≤ 0 h(\vec{x})\leq0 h(x )≤0 的外侧：（最优解取在边界上）（ h ( x ⃗ ∗ ) = 0 h(\vec{x}^*)=0 h(x ∗)=0）

那么解法其实就和等式约束优化问题的解是相同的。

对于这种情况，凸函数$f$的法线$\nabla f$指向$f$值增长的方向，凸函数$h$的法线$\nabla h$指向$h$值增长的方向：

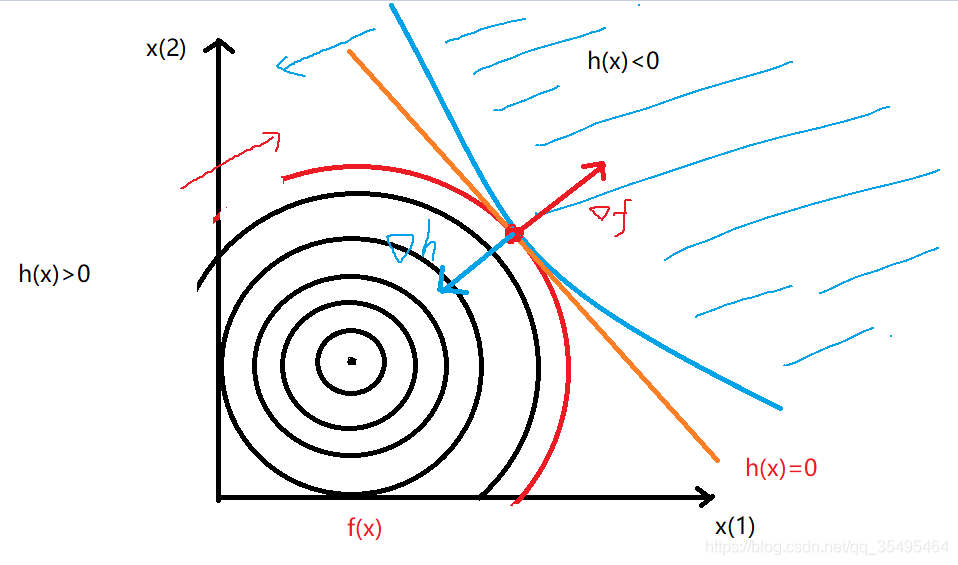
依旧是：
$$\nabla f+\lambda \nabla h=0$$
此时注意，$\nabla f$和$\nabla h$的方向是相反的，所以$\nabla f=-\lambda \nabla h$，即：$$\mathbf{\lambda }>0$$

（2）如果目标函数 f ( x ⃗ ) f(\vec{x}) f(x )在无约束下的极小值点在约束函数 h ( x ⃗ ) ≤ 0 h(\vec{x})\leq0 h(x )≤0 的内侧：（最优解取在 h ( x ⃗ ) ≤ 0 h(\vec{x})\leq0 h(x )≤0内部）（ h ( x ⃗ ∗ ) < 0 h(\vec{x}^*)<0 h(x ∗)<0）

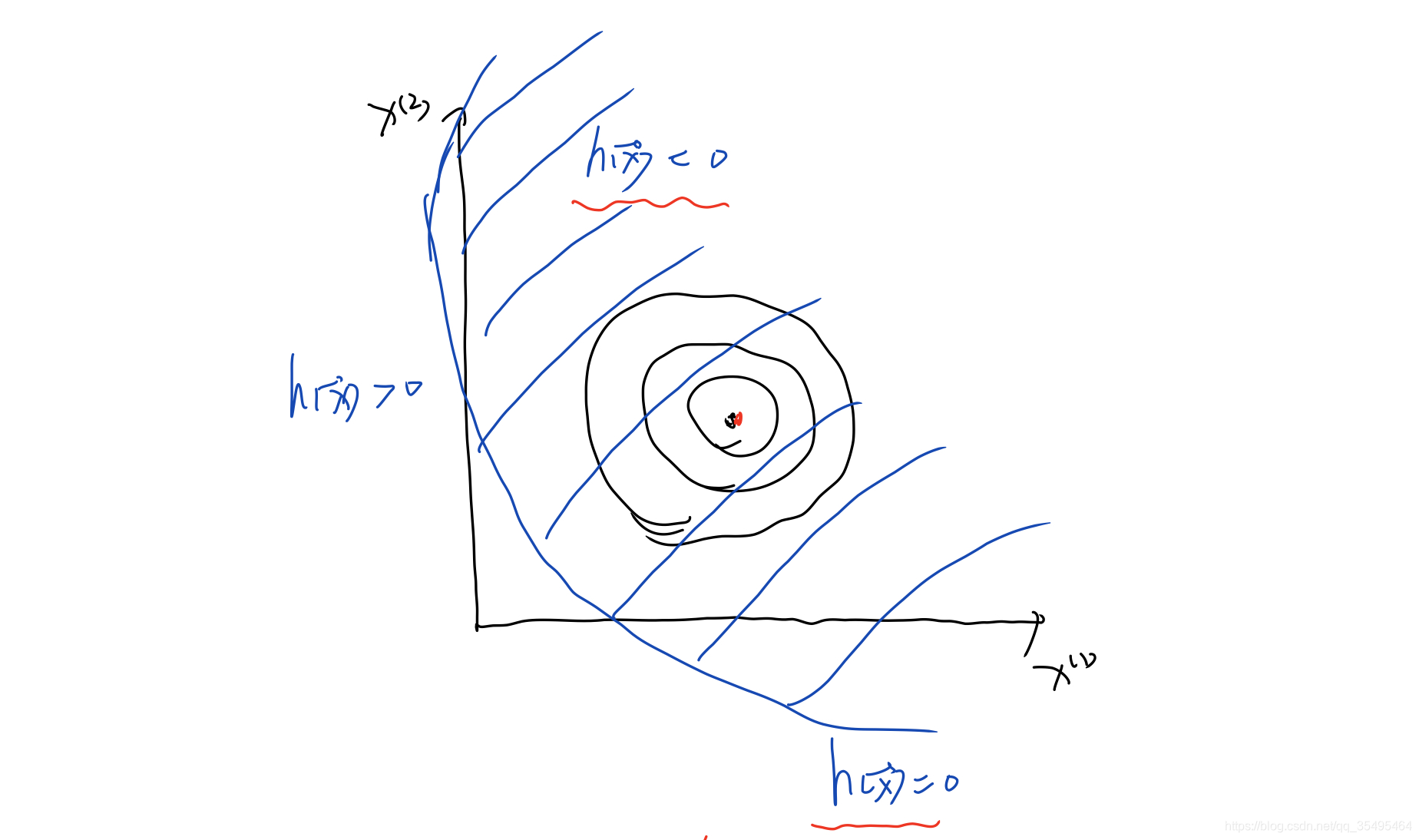
对于这种情况来说，约束条件就无效了。
h ( x ⃗ ) h(\vec{x}) h(x )不起作用，约束优化问题就退化为了无约束优化问题，因此 x ⃗ ∗ \vec{x}^* x ∗满足$\nabla f=0$且：$$\mathbf{\lambda }=0$$等同于求$min$ f ( x ⃗ ) f(\vec{x}) f(x )而已。

综上：

• 内部解：在约束条件无效的情形下， h ( x ⃗ ) h(\vec{x}) h(x )不起作用，约束优化问题退化为无约束优化问题，因此最优解 x ⃗ ∗ \vec{x}^* x ∗满足 $\nabla f=0$ 且 $\lambda =0$。
• 边界解：在约束条件有效的情形下，约束不等式变成等式 h ( x ⃗ ) = 0 h(\vec{x})=0 h(x )=0 ，这与前述拉格朗日乘数法的情况相同。我们可以知道，存在$\lambda$使得$\nabla f=-\lambda \nabla h$ ，但这里 $\lambda$的正负号是有其意义的。因为我们希望最小化$f$，梯度 $\nabla f$(函数 $f$ 在点 $x$的最陡上升方向)应该指向可行域的内部(因为我们的最优解最小值是在边界取得的)，但$\nabla h$指向 可行域的外部(即 h ( x ⃗ ) > 0 h(\vec{x})>0 h(x )>0 的区域，因为我们的约束是$\le 0$，因此 我们最终得到：$$\mathbf{\lambda }\ge 0$$称为对偶可行性(dual feasibility)。

并且，我们还得出：
无论是内部解还是边界解，都有 $$\lambda h(x)=0$$ 恒成立，称为互补松驰性（Complementary Slackness）。

【互补松驰性】：
当优化问题的不等式约束不等于0（$h(x)<0$）时，原始问题的约束是无效的，它无效，就得让$\lambda =0$来限制使之产生正向作用；否则就不用$\lambda$来限制了。

原始问题

经过以上一些基本的讨论，我们可以得到约束最优化问题的一般形式：

• 给出要优化的问题函数$f(x)$及要优化的变量 x ∈ R n x \in R^n x∈Rn
• $s.t.$：给出约束条件
• c i ( x ) c_i(x) ci​(x)：不等式约束（k个）
• h j ( x ) h_j(x) hj​(x)：等式约束（l个）

考虑最优化问题（基本形式）：
min ⁡ x ∈ R n f ( x ) \min_{x \in R^n}f(x) x∈Rnmin​f(x)
s . t . c i ( x ) ≤ 0 ， i = 1 , 2 , . . . , k s.t.\quad c_i(x)\leq0，i=1,2,...,k s.t.ci​(x)≤0，i=1,2,...,k
h j ( x ) = 0 ， j = 1 , 2 , . . . , l \qquad h_j(x)=0，j=1,2,...,l hj​(x)=0，j=1,2,...,l

引入广义拉格朗日函数：
L ( x , α , β ) = f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) L(x,\alpha,\beta)=f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum_{j=1}^{l}\beta_jh_j(x) L(x,α,β)=f(x)+i=1∑k​αi​ci​(x)+j=1∑l​βj​hj​(x)
后两项正是包含了优化问题的两个约束函数：

• $\alpha ,\beta$：拉格朗日乘子（k个，l个特征分量）（ α i ≥ 0 \alpha_i\geq0 αi​≥0）
• 满足不等式约束的所有k个$x$集合与满足等式约束的所有l个$x$集合，取交集得到满足约束条件的可行域
• 最优化问题的目的：在可行域中找一个使目标函数最小的$x$，得到最优解 x ∗ x^* x∗，此时的目标函数值为 p ∗ = f ( x ∗ ) p^*=f(x^*) p∗=f(x∗)

比如，我们考虑$x$的函数：
θ P ( x ) = min ⁡ x max ⁡ α , β : α i ≥ 0 L ( x , α , β ) \theta_P(x)=\min_x \max_{\alpha,\beta:\alpha_i\geq0}L(x,\alpha,\beta) θP​(x)=xmin​α,β:αi​≥0max​L(x,α,β)
$P$表示原始问题。

那么，为什么要设置成 c i ≤ 0 c_i\leq 0 ci​≤0 和 h j = 0 h_j=0 hj​=0 这两个约束条件呢？
首先我们想一下如果让$x$打破这两个约束，比如，存在某个 $i$ 使得 c i > 0 c_i>0 ci​>0，存在某个 $j$ 使得 h j ≠ 0 h_j\neq0 hj​​=0，那么我们就会发现，不对$x$的取值范围进行限制，会使得：
θ P ( x ) = max ⁡ α , β : α i ≥ 0 [ f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) ] = + ∞ \theta_P(x)=\max_{\alpha,\beta:\alpha_i\geq0}\left[ f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum_{j=1}^{l}\beta_jh_j(x)\right]=+\infty θP​(x)=α,β:αi​≥0max​[f(x)+i=1∑k​αi​ci​(x)+j=1∑l​βj​hj​(x)]=+∞
因为，一旦 α i ≥ 0 \alpha_i\geq0 αi​≥0， c i > 0 c_i>0 ci​>0， ∑ i = 1 k α i c i ( x ) \sum_{i=1}^{k}\alpha_ic_i(x) ∑i=1k​αi​ci​(x)会有机会趋于$+\infty$；同样，由于 h j ≠ 0 h_j\neq0 hj​​=0，且没有对 β j \beta_j βj​ 进行限制，总会能达到正无穷。

所以，只有当 $x$ 满足这两个约束条件式时，这个广义拉格朗日函数的极小极大问题才能等价于原始得最优化问题 ：
θ P ( x ) = min ⁡ x max ⁡ α , β : α i ≥ 0 L ( x , α , β ) = min ⁡ x { f ( x ) , c i ( x ) ≤ 0 , h j ( x ) = 0 + ∞ , O t h e r w i s e \theta_P(x)=\min_x \max_{\alpha,\beta:\alpha_i\geq0}L(x,\alpha,\beta)=\min_x \begin{cases} f(x), & \text{$c_i(x)\leq0,h_j(x)=0$} \\ +\infty, & \text{$Otherwise$} \end{cases} θP​(x)=xmin​α,β:αi​≥0max​L(x,α,β)=xmin​{f(x),+∞,​ci​(x)≤0,hj​(x)=0Otherwise​
那么，这样的话，我们再去考虑极小化问题：
min ⁡ x θ P ( x ) = min ⁡ x max ⁡ α , β : α i ≥ 0 L ( x , α , β ) \min_x\theta_P(x)=\min_x \max_{\alpha,\beta:\alpha_i\geq0}L(x,\alpha,\beta) xmin​θP​(x)=xmin​α,β:αi​≥0max​L(x,α,β)
就和我们原始的最优化问题是等价的了，即它俩有相同的解。
定义原始问题的最优值为： p ∗ = min ⁡ x θ P ( x ) p^*=\min_x\theta_P(x) p∗=xmin​θP​(x)

对偶问题

对偶问题其实就是原始问题的反过来。
此时对变量 $\alpha$ 和 $\beta$ 进行优化：
定义：
θ D ( α , β ) = min ⁡ x L ( x , α , β ) \theta_D(\alpha,\beta)=\min_xL(x,\alpha,\beta) θD​(α,β)=xmin​L(x,α,β)
再考虑极大化 θ D ( α , β ) = min ⁡ x L ( x , α , β ) \theta_D(\alpha,\beta)=\min_xL(x,\alpha,\beta) θD​(α,β)=minx​L(x,α,β) ，即：
max ⁡ α , β : α i ≥ 0 θ D ( α , β ) = max ⁡ α , β : α i ≥ 0 min ⁡ x L ( x , α , β ) \max_{\alpha,\beta:\alpha_i\geq0}\theta_D(\alpha,\beta)=\max_{\alpha,\beta:\alpha_i\geq0}\min_xL(x,\alpha,\beta) α,β:αi​≥0max​θD​(α,β)=α,β:αi​≥0max​xmin​L(x,α,β)
称为广义拉格朗日函数的极大极小问题。

同样，可以将极大极小问题表示为约束最优化问题：
max ⁡ α , β θ D ( α , β ) = max ⁡ α , β min ⁡ x L ( x , α , β ) \max_{\alpha,\beta}\theta_D(\alpha,\beta)=\max_{\alpha,\beta}\min_xL(x,\alpha,\beta) α,βmax​θD​(α,β)=α,βmax​xmin​L(x,α,β)
s . t . α i ≥ 0 , i = 1 , 2 , . . . , k s.t.\quad \alpha_i\geq0,i=1,2,...,k s.t.αi​≥0,i=1,2,...,k
称为原始问题的对偶问题。得到对偶问题的最优解 α ∗ \alpha^* α∗ 和 β ∗ \beta^* β∗ 以及最优值：
d ∗ = max ⁡ α , β : α i ≥ 0 θ D ( α , β ) d^*=\max_{\alpha,\beta:\alpha_i\geq0}\theta_D(\alpha,\beta) d∗=α,β:αi​≥0max​θD​(α,β)

【小总结】

• 原始问题：关于 $x$ 求目标函数的极小值，极小极大化拉格朗日函数
• 对偶问题：关于 $\alpha$ 和 $\beta$ 求目标函数极大值，极大极小化拉格朗日函数

原始问题和对偶问题的关系（3个定理）

定理C.1（ d ∗ d^* d∗和 p ∗ p^* p∗的关系）

【定理C.1】
若原始问题和对偶问题都有最优值，则：
d ∗ = max ⁡ α , β : α i ≥ 0 min ⁡ x L ( x , α , β ) ≤ min ⁡ x max ⁡ α , β : α i ≥ 0 L ( x , α , β ) = p ∗ d^*=\max_{\alpha,\beta:\alpha_i\geq0}\min_xL(x,\alpha,\beta)\leq\min_x \max_{\alpha,\beta:\alpha_i\geq0}L(x,\alpha,\beta)=p^* d∗=α,β:αi​≥0max​xmin​L(x,α,β)≤xmin​α,β:αi​≥0max​L(x,α,β)=p∗
【证明】：
首先我们知道，原始问题对 $x$ 的取值进行了两个条件式（可行域： c i ( x ) ≤ 0 c_i(x)\leq0 ci​(x)≤0, h j ( x ) = 0 h_j(x)=0 hj​(x)=0）的约束，而对偶问题则只对 $\alpha$ 进行了约束，对 $x$ 没有约束，所以，对于对偶问题中的 min ⁡ x L ( x , α , β ) \min_{x}L(x,\alpha,\beta) minx​L(x,α,β) ，通过它得到的极小值一定比原始问题中对 $x$ 加以限制而得到的极小值要小，这样就得到了一个不等式关系：
min ⁡ x L ( x , α , β ) ≤ min ⁡ x ∈ 可 行 域 L ( x , α , β ) \min_xL(x,\alpha,\beta)\leq\min_{x\in可行域}L(x,\alpha,\beta) xmin​L(x,α,β)≤x∈可行域min​L(x,α,β)
d ∗ = max ⁡ α , β : α i ≥ 0 min ⁡ x L ( x , α , β ) ≤ max ⁡ α , β : α i ≥ 0 min ⁡ x ∈ 可 行 域 L ( x , α , β ) d^*=\max_{\alpha,\beta:\alpha_i\geq0}\min_xL(x,\alpha,\beta)\leq\max_{\alpha,\beta:\alpha_i\geq0}\min_{x\in可行域}L(x,\alpha,\beta) d∗=α,β:αi​≥0max​xmin​L(x,α,β)≤α,β:αi​≥0max​x∈可行域min​L(x,α,β)
同时，满足了可行域，那么也即满足 c i ( x ) ≤ 0 c_i(x)\leq0 ci​(x)≤0、 h j ( x ) = 0 h_j(x)=0 hj​(x)=0，且 α i ≥ 0 \alpha_i\geq0 αi​≥0，那么表达式：
∑ i = 1 k α i c i ( x ) ≤ 0 , ∑ j = 1 l β j h j ( x ) = 0 \sum_{i=1}^{k}\alpha_ic_i(x)\leq0\quad,\quad\sum_{j=1}^{l}\beta_jh_j(x)=0 i=1∑k​αi​ci​(x)≤0,j=1∑l​βj​hj​(x)=0
也即：
L ( x , α , β ) = f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) ≤ f ( x ) L(x,\alpha,\beta)=f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum_{j=1}^{l}\beta_jh_j(x)\leq f(x) L(x,α,β)=f(x)+i=1∑k​αi​ci​(x)+j=1∑l​βj​hj​(x)≤f(x)
所以： d ∗ = max ⁡ α , β : α i ≥ 0 min ⁡ x L ( x , α , β ) ≤ max ⁡ α , β : α i ≥ 0 min ⁡ x ∈ 可 行 域 L ( x , α , β ) ≤ max ⁡ α , β : α i ≥ 0 min ⁡ x ∈ 可 行 域 f ( x ) d^*=\max_{\alpha,\beta:\alpha_i\geq0}\min_xL(x,\alpha,\beta)\leq\max_{\alpha,\beta:\alpha_i\geq0}\min_{x\in可行域}L(x,\alpha,\beta)\leq\max_{\alpha,\beta:\alpha_i\geq0}\min_{x\in可行域}f(x) d∗=α,β:αi​≥0max​xmin​L(x,α,β)≤α,β:αi​≥0max​x∈可行域min​L(x,α,β)≤α,β:αi​≥0max​x∈可行域min​f(x)
又 $f(x)$ 与 $\alpha ,\beta$ 无关：
max ⁡ α , β : α i ≥ 0 min ⁡ x ∈ 可 行 域 f ( x ) ≤ min ⁡ x ∈ 可 行 域 f ( x ) \max_{\alpha,\beta:\alpha_i\geq0}\min_{x\in可行域}f(x)\leq\min_{x\in可行域}f(x) α,β:αi​≥0max​x∈可行域min​f(x)≤x∈可行域min​f(x)
综上： d ∗ ≤ min ⁡ x ∈ 可 行 域 f ( x ) = p ∗ d^*\leq\min_{x\in可行域}f(x)=p^* d∗≤x∈可行域min​f(x)=p∗
证毕。

通过以上这个定理我们可以看出：
d ∗ ≤ p ∗ d^*\leq p^* d∗≤p∗
对偶问题的最优值提供了一个原始问题最优值的一个下界 ，也就是说，原始问题的最优值最小不能小于对偶问题的最优值。

我们发现这个不等式中有等号，那么等号的情况是什么样呢？

【推论C.1】
设 x ∗ , α ∗ , β ∗ x^*,\alpha^*,\beta^* x∗,α∗,β∗ 分别为原始问题和对偶问题的可行解，且 d ∗ = p ∗ d^*=p^* d∗=p∗ 时，则 x ∗ , α ∗ , β ∗ x^*,\alpha^*,\beta^* x∗,α∗,β∗ 分别是原始问题和对偶问题的最优解

定理C.2（ d ∗ = p ∗ d^*=p^* d∗=p∗的条件）

【定理C.2】
当原始问题满足：

• （1）原始问题是个凸优化问题
• （2）满足slater条件

则$⟹(充分条件)$： d ∗ = p ∗ d^*=p^* d∗=p∗（强对偶性）（ d ∗ ≤ p ∗ d^*\leq p^* d∗≤p∗为弱对偶性）

【凸优化问题】
我们的优化问题是在一个可行域中找到目标函数的最优值。那么如果我们的可行域集合是一个凸集，且要求的目标函数$f(x)$是一个凸函数，且要求的是目标函数的极小值，满足以上三个条件，就说这是一个凸优化问题。

• 凸集：凸集是一个集合$S$，若任意取两个点$x,y\in S$，如果这两个点的连线上的所有点也都在这个集合$S$内，则集合$S$称为凸集。
• 仿射函数：由 1 阶多项式构成的函数，一般形式为 $f(x)=Ax+b$，这里，$A$ 是一个 $m\times k$ 矩阵，$x$ 是一个$k$维向量，$b$是一个 $m$维 向量，实际上反映了一种从 $k$维到 $m$ 维的空间映射关系。
• 对于优化问题中的约束：如果不等式约束函数 c i ( x ) c_i(x) ci​(x)是凸函数，等式约束函数 h j ( x ) h_j(x) hj​(x)是仿射函数（关于$x$的线性函数）时，可行域集合就是一个凸集

【slater条件】
针对优化问题中约束条件的不等式约束条件的限制。
若$x$满足所有不等式约束条件的凸集的交集，且交集中存在相对内点，也就是说不等式约束是严格可行的（也即，存在$x$，对所有$i$，有 c i < 0 c_i<0 ci​<0）。

这样的话，就得出：
p ∗ = d ∗ = L ( x ∗ , α ∗ , β ∗ ) p^*=d^*=L(x^*,\alpha^*,\beta^*) p∗=d∗=L(x∗,α∗,β∗)
这个时候，就可以用解对偶问题代替解原始问题。

定理C.3（KKT条件）

其实，我们在上面拉格朗日乘子法部分讨论不等式约束优化问题过程中，就已经找到了KKT的所有条件。
对于前面部分探讨的优化问题：
min ⁡ x ∈ R n f ( x ) \min_{x\in R^n}f(x) x∈Rnmin​f(x)
$$s.t.h(x)\le 0$$
x = ( x ( 1 ) , x ( 2 ) ) T x=(x^{(1)},x^{(2)})^T x=(x(1),x(2))T
整合不等式约束条件的两种求解情况，最优解的必要条件包括拉格朗日乘子法的方程式、原始可行性、对偶可行性以及互补松驰性：

• 定常方程式(stationary equation)： ∇ X L = ∇ f + λ ∇ h = 0 \nabla_XL=\nabla f+\lambda\nabla h=0 ∇X​L=∇f+λ∇h=0
• 原始可行性（primal feasibility）：$h(x)\le 0$
• 对偶可行性(dual feasibility)：$\lambda \ge 0$
• 互补松驰性（complementary slackness）：$\lambda h(x)=0$

推广到多个等式与不等式约束式的情况：
【定理C.3：KKT条件】
当原始问题满足强对偶性（ p ∗ = d ∗ p^*=d^* p∗=d∗）的时候，可以使用KKT条件进行求最优解 x ∗ , α ∗ , β ∗ x^*,\alpha^*,\beta^* x∗,α∗,β∗。

原始最优化问题：
min ⁡ x ∈ R n f ( x ) \min_{x \in R^n}f(x) x∈Rnmin​f(x)
s . t . c i ( x ) ≤ 0 ， i = 1 , 2 , . . . , k s.t.\quad c_i(x)\leq0，i=1,2,...,k s.t.ci​(x)≤0，i=1,2,...,k
h j ( x ) = 0 ， j = 1 , 2 , . . . , l \qquad h_j(x)=0，j=1,2,...,l hj​(x)=0，j=1,2,...,l

引入广义拉格朗日函数：
L ( x , α , β ) = f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) L(x,\alpha,\beta)=f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum_{j=1}^{l}\beta_jh_j(x) L(x,α,β)=f(x)+i=1∑k​αi​ci​(x)+j=1∑l​βj​hj​(x)

则KKT条件（充要条件）：

• ∇ x L ( x ∗ , α ∗ , β ∗ ) = 0 \nabla_xL(x^*,\alpha^*,\beta^*)=0 ∇x​L(x∗,α∗,β∗)=0
• α i ∗ c i ( x ∗ ) = 0 , i = 1 , 2 , . . . , k \alpha_i^*c_i(x^*)=0,\quad i=1,2,...,k αi∗​ci​(x∗)=0,i=1,2,...,k
• c i ( x ∗ ) ≤ 0 , i = 1 , 2 , . . . , k c_i(x^*)\leq0,\quad i=1,2,...,k ci​(x∗)≤0,i=1,2,...,k
• α i ∗ ≥ 0 , i = 1 , 2 , . . . , k \alpha_i^*\geq0,\quad i=1,2,...,k αi∗​≥0,i=1,2,...,k
• h j ( x ∗ ) = 0 , j = 1 , 2 , . . . , l h_j(x^*)=0,\quad j=1,2,...,l hj​(x∗)=0,j=1,2,...,l

【注】
α i ∗ c i ( x ∗ ) = 0 , i = 1 , 2 , . . . , k \quad \quad\alpha_i^*c_i(x^*)=0,\quad i=1,2,...,k αi∗​ci​(x∗)=0,i=1,2,...,k也称为KKT的对偶互补条件（互补松弛性）：

• 若 α i ∗ > 0 \alpha_i^*>0 αi∗​>0，则 c i ( x ∗ ) = 0 c_i(x^*)=0 ci​(x∗)=0

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！