LeetCode——587 安装栅栏(JAVA)

在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时，花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。

示例 1:

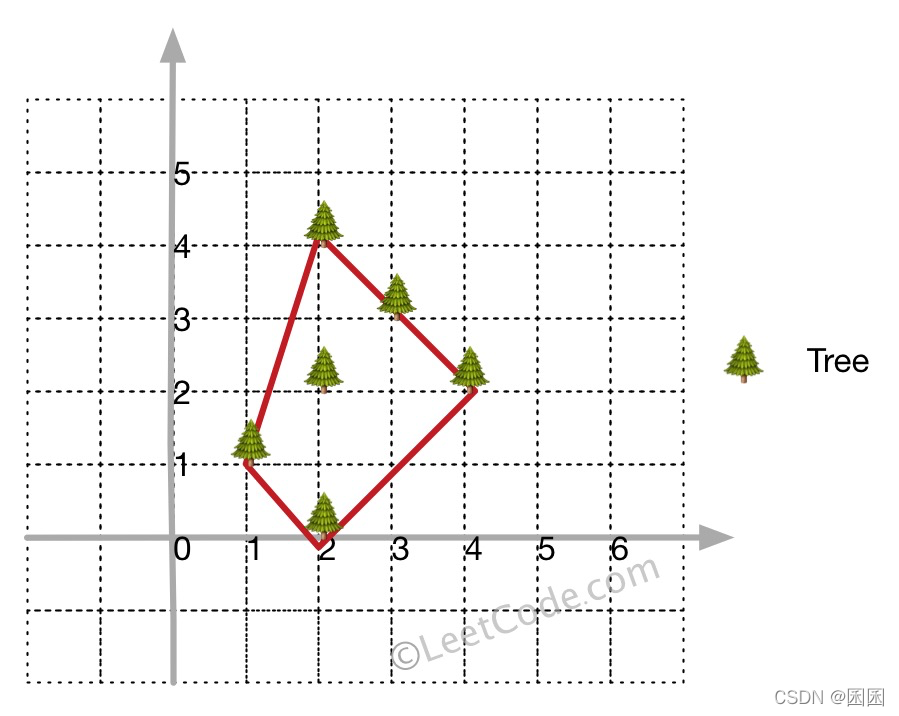
输入: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出: [[1,1],[2,0],[4,2],[3,3],[2,4]]

解释：

示例 2:

输入: [[1,2],[2,2],[4,2]]
输出: [[1,2],[2,2],[4,2]]

注意:

• 所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
• 输入的整数在 0 到 100 之间。
• 花园至少有一棵树。
• 所有树的坐标都是不同的。
• 输入的点没有顺序。输出顺序也没有要求。

思路

第一次碰到凸包的问题，这里用的Jarvis算法，因为理解起来比较简单。但是在具体手写代码实现的过程中，还是碰到了不少的问题。

Jarvis算法的主要思路就是，先从最左端的点开始（作为p），然后寻找其他点作为q，在固定完p和q之后，再在剩余的点中寻找r。
然后，计算 p q → \overrightarrow{pq} pq ​和 q r → \overrightarrow{qr} qr ​的叉积：
如果叉积>=0，则说明此时的点r在 p q → \overrightarrow{pq} pq ​的左侧（右手定则，此时，从 p q → \overrightarrow{pq} pq ​到 q r → \overrightarrow{qr} qr ​逆时针旋转的角度<=180度）；反之，则说明此时的点r在 p q → \overrightarrow{pq} pq ​的右侧。

因此，为了能找到一个凸包，就需要确定此时形成的 p q → \overrightarrow{pq} pq ​，它能否将所有的r都放在同一侧（本题是左侧）。如果能，则将这个q作为下一个p（p是答案集合中的点），并进入下一轮循环寻找新的点q；如果不能，则需要继续寻找点q。
至于算法结束的位置，就是当成为一个环时，算法就结束了。也就是说，当寻找得到的点q又是起始位置最左端的点时，结束这个算法。

然后说一下本题可能遇到的坑点和我的解决办法：

1. 输入可能只有一个点，这种情况特判即可，即：

if(trees.length==1) return trees;

2. 如果直接对输入的坐标按照Jarvis算法求凸包，可能会漏掉在同一条直线上的情况，比如在示例1中，可能会漏掉(3, 3)这个点，因为它在(4, 2)和(2, 4)所构成的直线上。
   我的解决办法是：如果碰到一个可行的点q，那么，将它从未选择的点中删去后，将这些未选择的点，按照到点q的距离从小到大排序，这样，就不会漏掉一条直线上的点了。
   比如，在我寻找到(4, 2)作为点q这样一个可行点后，我对剩下的(2, 2)、(3, 3)、(2, 4)来排个序，靠近(4, 2)的点我先去遍历，这样的话，就不会漏掉可行解了。
3. 因为算法结束的位置是再次寻找到起点（也就是最左端的点），因此，在上述排序的时候，我们需要把起点抛开，然后排完序再加进去（也就是让起点始终保持在最后一个位置）。否则的话，在示例2中，如果找到(2, 2)这个点后，按照距离排序，就会直接找到起点(1, 2)从而结束整个算法，这样就漏掉了(4, 2)这个点。
4. 关于起点：最左端的点指的是横坐标（x）最小的那个点，而不应该是最左下角的点（x和y都小）。

代码

class Solution {static class Point{int x;int y;double dis; // 其他点到p的距离Point(){}Point(int xx, int yy){x = xx;y = yy;}public int getX(){return x;}public int getY(){return y;}}public double dis(Point p, Point q){int x1 = p.getX();int x2 = q.getX();int y1 = p.getY();int y2 = q.getY();return Math.sqrt(Math.pow((x1-x2), 2)+Math.pow((y1-y2), 2));}public boolean cross(Point p, Point q, Point r){int x1 = q.getX()-p.getX();int y1 = q.getY()-p.getY();int x2 = r.getX()-q.getX();int y2 = r.getY()-q.getY();int result = x1*y2 - y1*x2;return result >= 0;}public int[][] outerTrees(int[][] trees) {if(trees.length==1) return trees;else{List<Point> choose = new ArrayList<>();List<Point> notChoose = new ArrayList<>();int leftX = 110, leftY = 110;Point left = new Point();for(int[] tree : trees){int tmpX = tree[0];int tmpY = tree[1];Point tmp = new Point(tmpX, tmpY);notChoose.add(tmp);if (tmpX < leftX) {leftX = tmpX;leftY = tmpY;left = tmp;}}Point p = left;Comparator<Point> comparator = new Comparator<Point>() {@Overridepublic int compare(Point o1, Point o2) {if(o1.dis<o2.dis) return -1;else if(o1.dis>o2.dis) return 1;else return 0;}};notChoose.remove(left);for(Point point : notChoose){point.dis = dis(p, point);}notChoose.sort(comparator);notChoose.add(left);for(int i=0;i<notChoose.size();i++){Point q = notChoose.get(i);if(q==p) continue;boolean flag = true;for(Point r : notChoose){if(q!=r){if(!cross(p, q, r)) flag = false;}}if(flag){choose.add(q);notChoose.remove(q);if(q.getX()==leftX && q.getY()==leftY) break; //算法结束p = q;i = -1;notChoose.remove(left);for(Point point : notChoose){point.dis = dis(p, point);}notChoose.sort(comparator);notChoose.add(left);}}int[][] result = new int[choose.size()][2];for(int i=0;i<choose.size();i++){int tmpX = choose.get(i).getX();int tmpY = choose.get(i).getY();result[i][0] = tmpX;result[i][1] = tmpY;}return result;}}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！