[CSP-J2020] 直播获奖

题目描述

NOI2130 即将举行。为了增加观赏性，CCF 决定逐一评出每个选手的成绩，并直播即时的获奖分数线。本次竞赛的获奖率为 $w\%$，即当前排名前 $w\%$ 的选手的最低成绩就是即时的分数线。

更具体地，若当前已评出了 $p$ 个选手的成绩，则当前计划获奖人数为 $\max (1,\lfloor p\ast w\%\rfloor )$，其中 $w$ 是获奖百分比，$\lfloor x\rfloor$ 表示对 $x$ 向下取整，$\max (x,y)$ 表示 $x$ 和 $y$ 中较大的数。如有选手成绩相同，则所有成绩并列的选手都能获奖，因此实际获奖人数可能比计划中多。

作为评测组的技术人员，请你帮 CCF 写一个直播程序。

输入格式

第一行有两个整数 $n,w$。分别代表选手总数与获奖率。
第二行有 $n$ 个整数，依次代表逐一评出的选手成绩。

输出格式

只有一行，包含 $n$ 个非负整数，依次代表选手成绩逐一评出后，即时的获奖分数线。相邻两个整数间用一个空格分隔。

样例 #1

样例输入 #1

10 60
200 300 400 500 600 600 0 300 200 100

样例输出 #1

200 300 400 400 400 500 400 400 300 300

样例 #2

样例输入 #2

10 30
100 100 600 100 100 100 100 100 100 100

样例输出 #2

100 100 600 600 600 600 100 100 100 100

提示

样例 1 解释

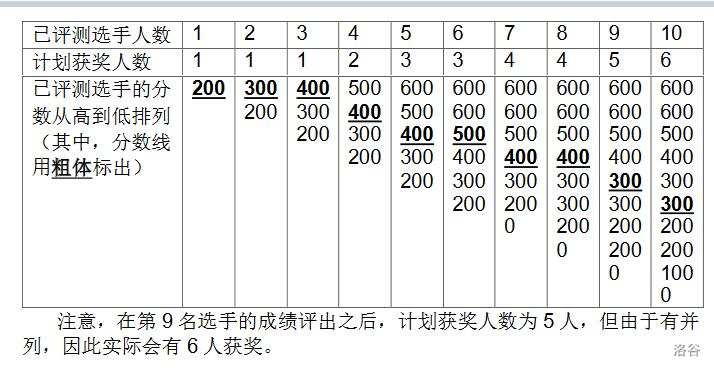
数据规模与约定

各测试点的 $n$ 如下表：

对于所有测试点，每个选手的成绩均为不超过 $600$ 的非负整数，获奖百分比 $w$ 是一个正整数且 $1\le w\le 99$。

提示

在计算计划获奖人数时，如用浮点类型的变量（如 C/C++ 中的 float 、 double，Pascal 中的 real 、 double 、 extended 等）存储获奖比例 $w\%$，则计算 $5\times 60\%$ 时的结果可能为 $3.000001$，也可能为 $2.999999$，向下取整后的结果不确定。因此，建议仅使用整型变量，以计算出准确值。

解析

本题可以采用每次排序的方式，如果使用快排，时间复杂度为O(N^2 lgN),理论上可以解决30%的数据，如果采用插入排序的方式，时间复杂度为O(N^2),理论上可以解决50%的数据。
由于本题分数范围为0-600，所以可以采用桶排序，时间复杂度为O(600*N），可以解决所有数据，详见代码：

#include
using namespace std;
int a[605];
int n,w;
int main() {scanf("%d %d",&n,&w);for (int i=1;i<=n;i++){int x;scanf("%d",&x);a[x]++;//桶排序int m=max(1,i*w/100);//计算获奖名额int sum=0;for (int j=600;j>=0;j--){//累计高分人数sum+=a[j];if (sum>=m){printf("%d ",j);break;}}}return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！