证据理论

• 证据理论介绍
• 概率分配函数
• 信任函数
• 似然函数
• 概率分配函数的正交和
• 特定的概率分配函数
• 基于特定的概率分配函数的不确定性推理模型
• 信任度函数
• 知识不确定性的表示
• 证据的不确定性的表示
• 不确定性的传递算法
• 推理实例（一）
• 推理实例（二）
• 证据理论推理的特点

证据理论介绍

• 证据理论 (Theory of Evidence) 也称为 D - S(Dempster-Shafer) 理论。
• 能够区分 “不确定” 与 “不知道” 的差异，并能够处理由 “不知道” 引起的不确定性，具有较大的灵活性。
• 在 D - S 理论中，知识以产生式规则的形式表示，证据和结论以集合形式表示。D - S 理论采用集合来表示命题，为此，首先应该建立命题与集合之间的一一对应关系，把命题的不确定性问题转化为集合的不确定性问题。
• 在证据理论中，D 的任何一个子集 A 都对应于一个关于 x 的命题，称该命题为 “ x 的值在 A 中 ” 。

概率分配函数

信任函数

似然函数

概率分配函数的正交和

特定的概率分配函数

基于特定的概率分配函数的不确定性推理模型

信任度函数

知识不确定性的表示

证据的不确定性的表示

不确定性的传递算法

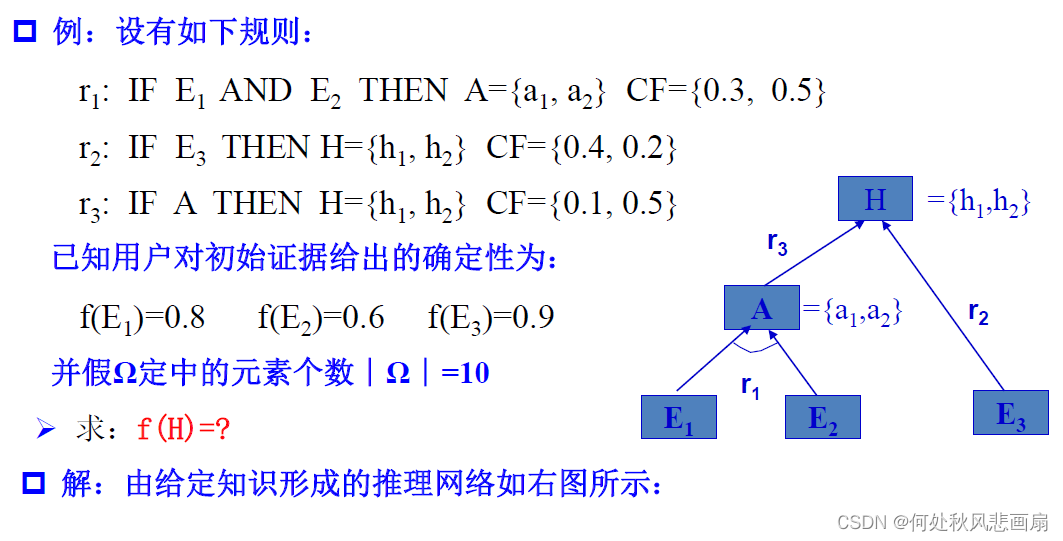
推理实例（一）

推理实例（二）

证据理论推理的特点

• 优点：
  • 1.能满足比概率更弱的公理系统，能处理由“不知道”所引起的不确定性；
  • 2.子集可以是多个元素的集合，因而知识的结论部分可以是更一般的假设，有利于领域专家在不同细节、不同层次上进行知识表示。
• 缺点：
  • 1.要求样本空间中的元素满足互斥条件，在实际系统中不易实现；
  • 2.要求给出的概率分配数太多，计算比较复杂。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！