D-S 证据理论
一.D-S证据理论引入
诞生:
D-S证据理论的诞生:起源于20世纪60年代的哈佛大学数学家A.P. Dempster利用上、下限概率解决多值映射问题,1967年起连续发表一系列论文,标志着证据理论的正式诞生。
形成:
Dempster的学生G.shafer对证据理论做了进一步研究,引入信任函数概念,形成了一套“证据”和“组合”来处理不确定性推理的数学方法
D-S理论是对贝叶斯推理方法推广,主要是利用概率论中贝叶斯条件概率来进行的,需要知道先验概率。而D-S证据理论不需要知道先验概率,能够很好地表示“不确定”,被广泛用来处理不确定数据。
适用于:信息融合、专家系统、情报分析、法律案件分析、多属性决策分析
二.D-S证据理论的基本概念
定义1 基本概率分配(BPA)
![设U为以识别框架,则函数m:2u→[0,1]m:2u→[0,1]满足下列条件:(1)m(ϕ)=0m(ϕ)=0(2)∑A⊂Um(A)=1∑A⊂Um(A)=1时称m(A)=0m(A)=0为A的基本赋值,m(A)=0m(A)=0表示对A的信任程度也称为mass函数。](https://img-blog.csdnimg.cn/20181107173915357.png)
定义2 信任函数 (Belief Function)
![Bel:2u→[0,1]Bel:2u→[0,1]Bel(A)=∑B⊂Am(B)=1 (∀A⊂U)Bel(A)=∑B⊂Am(B)=1 (∀A⊂U)表示A的全部子集的基本概率分配函数之和](https://img-blog.csdnimg.cn/20181107173939700.png)
定义3 似然函数(plausibility Function)

定义4 信任区间

三.D-S证据理论的组合规则
m个mass函数的Dempster合成规则

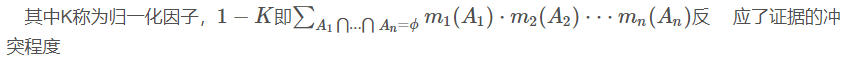
四.判决规则

五.D-S证据理论存在的问题
(一)无法解决证据冲突严重和完全冲突的情况
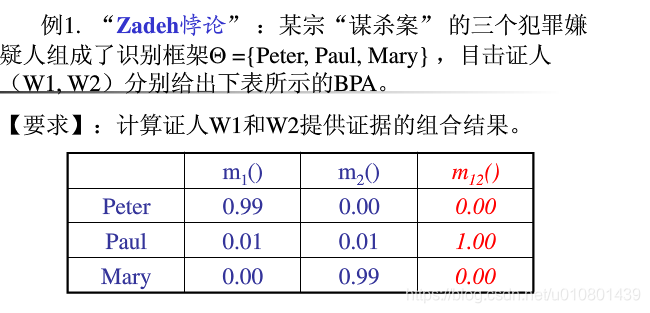
该识别框架为{Peter,Paul,Mary},基本概率分配函数为m{Peter},m{Paul},m{Mary}
由D-S证据理论的基本概念和组合规则进行解析



可以看出虽然在W1,W2目击中,peter和mary都为0.99,但是存在严重的冲突,造成合成之后的Bel函数值为0,这显然与实际情况不合,更极端的情况如果W1中m{peter)=1,W2中m{Mary}=1,则归一化因子K=0,D-S组合规则无法进行
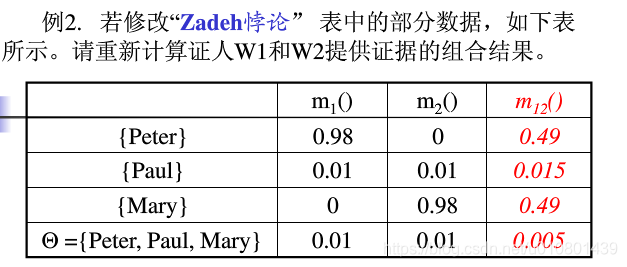






(二)难以辨识模糊程度
由于证据理论中的证据模糊主要来自于各子集的模糊度。根据信息论的观点,子集中元素的个数越多,子集的模糊度越大
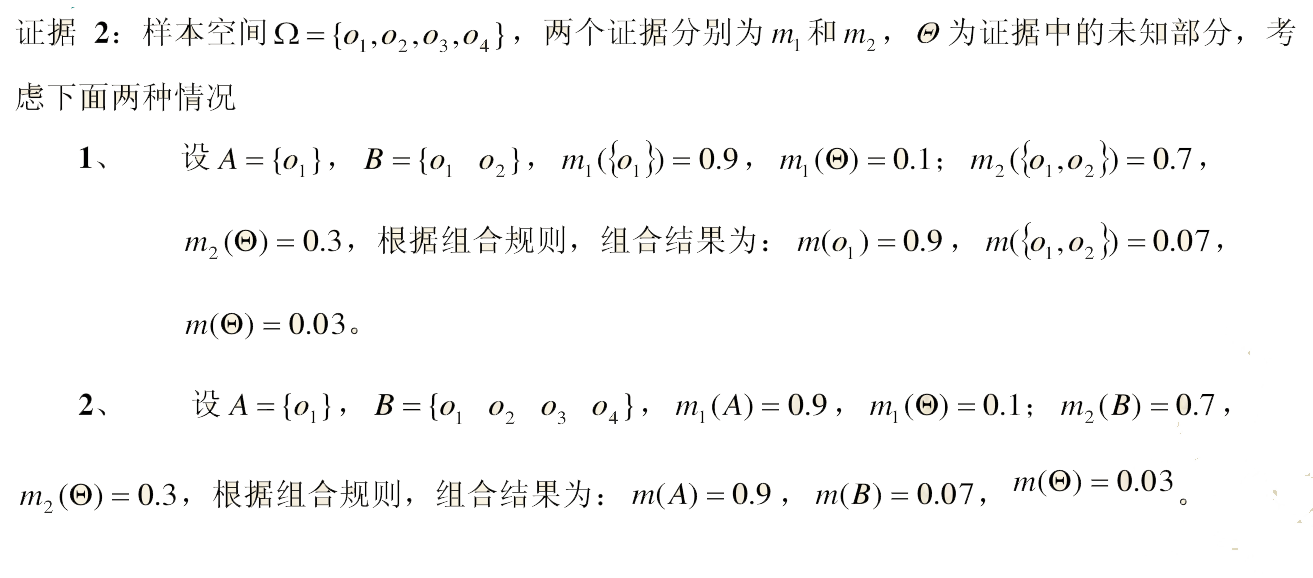
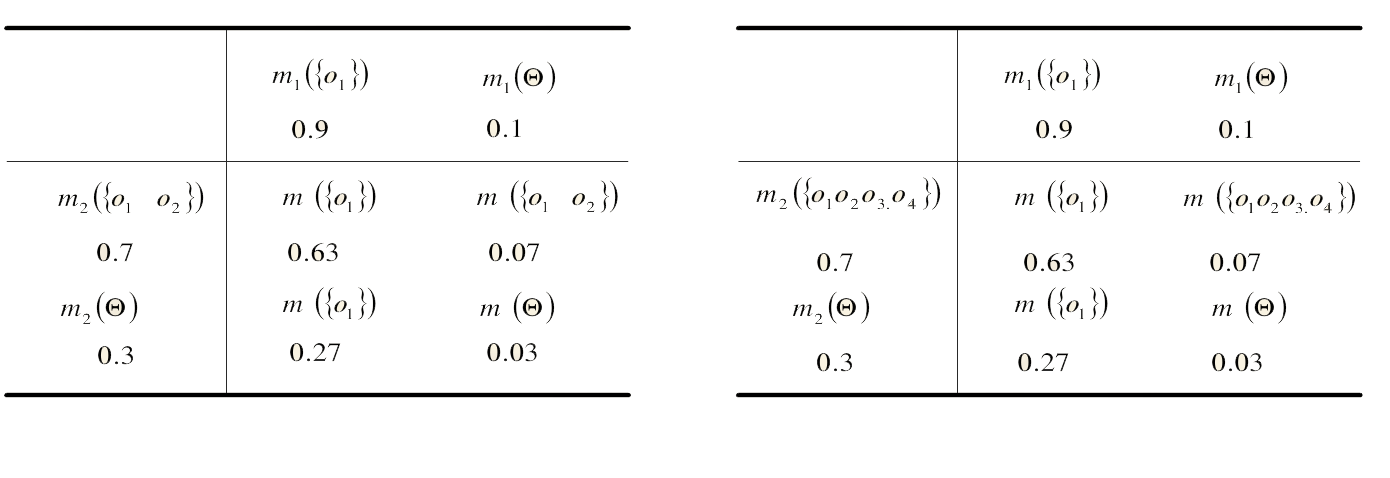
(三)基本概率分配函数的微小变化会使组合结果产生急剧变化


本文转自: 链接地址
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!