【技巧】37%法则（rand()随机）

Introduction

在我很小的时候，就曾在《意林》或者其他什么杂志上读过一则小故事：苏格拉底叫人穿过一片麦地，不走回头路且只能选取一个的情况下，找到最大的麦穗。

故事结尾好像是很多人都无功而返，或者是抱怨自己过早选中而悔恨。不过不重要了，故事的结尾能领悟出什么道理有的时候取决于编辑希望我们明白什么道理。

再后来，我又在不同场合听到过多次这样的故事，无非就是做实验的人变成了柏拉图、亚里士多德或者其他人，麦穗变成了葡萄、玉米之类的。

这些问题的解都是一致的，即记录下前37%最大值不选择，此后若遇到大于等于该值的，则选中。这个策略好像能用概率统计的知识来证明，我似乎看过，但却记不清了，并且也不想查阅有关资料，因为这不是重点。

重点来了，我记得这个法则被人用到了选择对象上了！即假设某一年龄段为择偶期间，观察前37%，记下最喜欢的那个，之后遇到相同的或者更好的果断结婚！我们假设这段时间是15-35岁好了，20*0.37=7.4，即15-22.4观察，后面果断入手。

那么问题来了，后面再也遇到大于等于的对象了呢？

Experiment

1、简单模拟选择过程

#include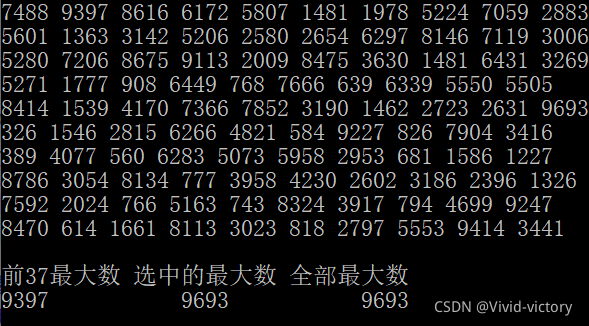 
#include 
#include 
#include 
using namespace std;
void Random(int *a,int n)//最大范围：0~32767
{srand(time(0));for(int i=0; i<n; i++) {a[i]=rand()%10001;}
}
int main()
{int n=100,maxn37=0,ans = -1;int a[n];Random(a,n);for(int i=0; i<n; i++) {cout<<a[i]<<" ";if(i%10==9) cout<<endl;if(i<37 && a[i]>maxn37) maxn37 = a[i];if(i>=37 && a[i] >= maxn37&&ans==-1) {ans = a[i];}}cout<<endl<<"前37最大数 "<<"选中的最大数 "<<"全部最大数  "<<endl;printf("%-15d%-15d%-15d\n",maxn37,ans,*max_element(a,a+n));return 0;
}

随便一试，效果不错，那选取的样本多一点呢？

2、多重人生

#include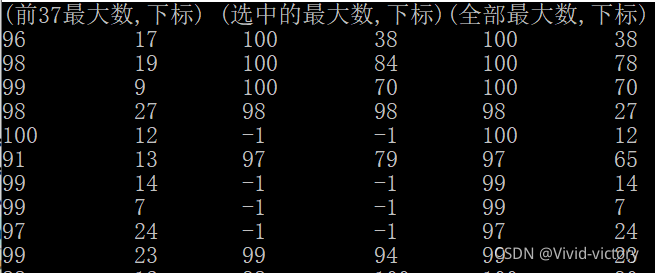 
#include 
#include 
#include 
using namespace std;void Random(int *a,int n)//最大范围：0~32767
{for(int i=0; i<n; i++) {a[i]=rand()%100+1;}
}int main()
{int life = 100, fail = 0,success = 0;cout<<"(前37最大数,下标) "<<"(选中的最大数,下标)"<<"(全部最大数,下标)"<<endl;while(life--) {pair<int,int> maxn37(-1,-1),ans(-1,-1),maxn(-1,-1); //（最大值，坐标）int n=100;int a[n];Random(a,n);for(int i=0; i<n; i++) {if(i<37 && a[i] > maxn37.first) {maxn37 = make_pair(a[i],i+1);}if(i>=37 && a[i] >= maxn37.first) {ans  = make_pair(a[i],i+1);}if(maxn.first < a[i]) {maxn = make_pair(a[i],i+1);}}if(ans.first == -1)  fail++;if(ans.first == maxn.first) success++;printf("%-10d %-8d %-10d %-8d %-10d %-8d\n",\maxn37.first,maxn37.second,ans.first,ans.second,maxn.first,maxn.second);}cout<<fail<<endl;cout<<success<<endl;return 0;
}

只能说人和人之间的差距太大了！
从概率上这个策略或许是最优的，但我们的人生只有一次，过度痴迷最优解，只能孤独终老，得到-1的结局。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！