P4467 [SCOI2007]k短路(A*)
题目描述
有nn个城市和mm条单向道路,城市编号为11到nn。每条道路连接两个不同的城市,且任意两条道路要么起点不同要么终点不同,因此nn和mm满足m \le n(n-1)m≤n(n−1)。
给定两个城市a和b,可以给a到b的所有简单路(所有城市最多经过一次,包括起点和终点)排序:先按长度从小到大排序,长度相同时按照字典序从小到大排序。你的任务是求出a到b的第kk短路
输入输出格式
输入格式:
输入第一行包含五个正整数n, m, k, a, b。
以下m行每行三个整数u, v, l,表示从城市u到城市v有一条长度为l的单向道路。
输出格式:
如果a到b的简单路不足k条,输出No,否则输出第k短路:从城市a开始依次输出每个到达的城市,直到城市b,中间用减号"-"分割。
输入输出样例
输入样例#1: 复制
5 20 10 1 5 1 2 1 1 3 2 1 4 1 1 5 3 2 1 1 2 3 1 2 4 2 2 5 2 3 1 1 3 2 2 3 4 1 3 5 1 4 1 1 4 2 1 4 3 1 4 5 2 5 1 1 5 2 1 5 3 1 5 4 1
输出样例#1: 复制
1-2-4-3-5
输入样例#2: 复制
4 6 1 1 4 2 4 2 1 3 2 1 2 1 1 4 3 2 3 1 3 4 1
输出样例#2: 复制
1-2-3-4
输入样例#3: 复制
3 3 5 1 3 1 2 1 2 3 1 1 3 1
输出样例#3: 复制
No
说明
第一个例子有5个城市,所有可能出现的道路均存在。从城市1到城市5一共有5条简单路,排序如下:
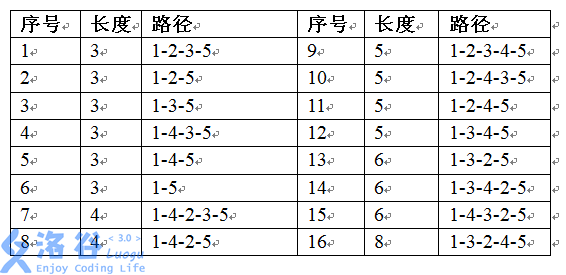
20%的数据满足:n<=5
40%的数据满足:n<=30
100%的数据满足:2<=n<=50, 1<=k<=200
解题思路
菜鸡不会正解,只能A*+特判(打表) , 有个测试点MLE了,打表过的,还写了贼久。
首先,建图,建一个正向图和一个反向图,用反向图求b到所有城市的最短距离。然后用正向图bfs。bfs有一个性质,如果点k第i次出队,那么当前距离就是到点k的第i小距离。因为各个边的权值都不同,所以我们用优先队列。但是,如果就这么直接bfs,太慢了,所以就用到A*,当前经过距离+从当前点到b点的最短距离 = 从当前路径来到b的最短距离。让 从当前路径来到b的最短距离 排在队首,就可以省去很多步骤。
代码如下
#include
#include
#include
#include
#include
#define maxn 55
#define INF 0x3f3f3f3f
using namespace std;
int dis[maxn];
struct node{int x; //城市编号 int d; //当前经过距离 string way; //路径 node(int x, int d, string w): x(x), d(d), way(w){ }bool operator<(const node& a)const{if(d + dis[x] != a.d + dis[a.x]) //距离短 return (d + dis[x]) > (a.d + dis[a.x]);else if(way != a.way) //字典序 return way > a.way;else //本身编号小 return x > a.x;}
};
struct T{int r, dis;T(int r, int dis): r(r), dis(dis){ }
};
vector g1[maxn]; //正图
vector g2[maxn]; //反图
int n, m, k, s, t;
priority_queue que;
void bfs()
{ string str;str += (char)s;que.push(node(s, 0, str));while(!que.empty()){node top = que.top();que.pop();int x = top.x;int d = top.d;if(x == t){k --;if(!k){string temp = top.way;cout << s;for(int i = 1; i < temp.size(); i ++){cout << "-" << (int)temp[i] ;}cout << endl;return;}}else {for(int i = 0; i < g1[x].size(); i ++){int r = g1[x][i].r;char temp = r;if(top.way.find(temp) == -1) //没有重复经过的点 que.push(node(r, d + g1[x][i].dis, top.way + (char)r));}} }cout << "No" << endl;
}
bool spfa()
{memset(dis, 0x7f, sizeof(dis));dis[t] = 0;bool vis[maxn] = {0};queue que;que.push(t);vis[t] = true;bool flg = false;while(!que.empty()){int top = que.front();que.pop();vis[top] = false;if(top == s)flg = true;for(int i = 0; i < g2[top].size(); i ++){int r = g2[top][i].r;int d = g2[top][i].dis;if(dis[r] > dis[top] + d){dis[r] = dis[top] + d;if(!vis[r]){vis[r] = true;que.push(r);}}}}return flg;
}
int main()
{cin >> n >> m >> k >> s >> t;if(n==30&&m==759){puts("1-3-10-26-2-30"); return 0;} //特判 for(int i = 0; i < m; i ++){int u, v, l;cin >> u >> v >> l;g1[u].push_back(T(v, l));g2[v].push_back(T(u, l));}if(!spfa()){cout << "No" << endl;return 0;}bfs();return 0;
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!