chatgpt赋能python:如何使用Python求圆周率?
如何使用Python求圆周率?
圆周率(π)是数学中一个重要的常数,它代表着圆的周长与直径的比值,通常用π表示。圆周率的计算一直是数学家们关注的问题,也是计算机编程中的一个经典问题。今天我们将介绍如何使用Python来计算圆周率。
什么是Python?
首先,让我们正式介绍一下Python。Python是一种高级编程语言,由Guido van Rossum于1989年开发。Python易于学习、阅读和编写,因此它成为了一个流行的编程语言。Python被广泛应用于数据科学、机器学习、人工智能、网站开发等领域。
方法一:蒙特卡罗方法
蒙特卡罗方法是一种基于随机抽样的方法,用于估算数学问题。在计算圆周率中,我们可以使用蒙特卡罗方法来近似计算π的值。
这种方法的基本思路是,我们在一个正方形中绘制一个圆,然后在这个正方形中随机生成点。如果这个点在圆内,则计数器加1,否则不加。通过计数器值的比例,即可估算圆的面积和π的值。
下面是Python代码实现:
from random import randrangedef pi_monte_carlo(n):count = 0for i in range(n):x = randrange(-1, 1)y = randrange(-1, 1)if x ** 2 + y ** 2 <= 1:count += 1pi = 4 * (count / n)return pi
方法二:牛顿-莱布尼兹公式
牛顿-莱布尼兹公式是微积分中的一个公式,可以用于计算圆周率。这个公式的表述是,如果f(x)是区间[a,b]上一个连续可微的函数,则[a,b]上f(x)的定积分等于F(b)-F(a),其中F(x)是f(x)的一个原函数。当f(x)是sin(x)时,可以用这个公式来计算π的值。
下面是Python代码实现:
from math import sindef pi_newton_leibniz(n):pi = 0for i in range(1, n+1):pi += (((-1)**(i+1)) / (2*i-1)) * sin((2*i-1) * 1)return 4 * pi
结论
通过蒙特卡罗方法和牛顿-莱布尼兹公式,我们可以使用Python计算圆周率。这两种方法各有优缺点,其中蒙特卡罗方法在处理高维问题时更有效,而牛顿-莱布尼兹公式则更加精确。当然,除了这两种方法外,还有其他的方法可以用于计算圆周率,读者可以进一步研究。希望这篇文章对您有所帮助!
最后的最后
本文由chatgpt生成,文章没有在chatgpt生成的基础上进行任何的修改。以上只是chatgpt能力的冰山一角。作为通用的Aigc大模型,只是展现它原本的实力。
对于颠覆工作方式的ChatGPT,应该选择拥抱而不是抗拒,未来属于“会用”AI的人。
🧡AI职场汇报智能办公文案写作效率提升教程 🧡 专注于AI+职场+办公方向。
下图是课程的整体大纲
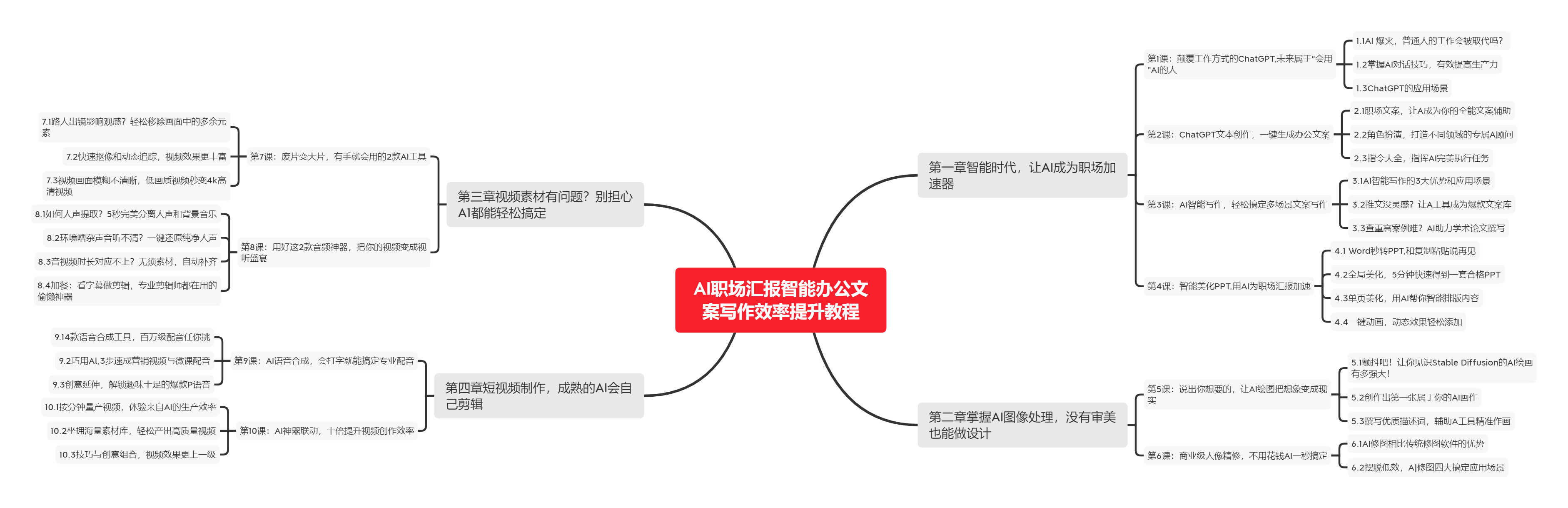

下图是AI职场汇报智能办公文案写作效率提升教程中用到的ai工具

🚀 优质教程分享 🚀
- 🎄可以学习更多的关于人工只能/Python的相关内容哦!直接点击下面颜色字体就可以跳转啦!
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| 🧡 AI职场汇报智能办公文案写作效率提升教程 🧡 | 进阶级 | 本课程是AI+职场+办公的完美结合,通过ChatGPT文本创作,一键生成办公文案,结合AI智能写作,轻松搞定多场景文案写作。智能美化PPT,用AI为职场汇报加速。AI神器联动,十倍提升视频创作效率 |
| 💛Python量化交易实战 💛 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
| 🧡 Python实战微信订餐小程序 🧡 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!