数据结构进阶篇，二叉树构造专题

105. 从前序与中序遍历序列构造二叉树

  「题目：」

  给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

  「示例：」

  输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]，输出: [3,9,20,null,null,15,7]。

  「解题思路：」

  由于二叉树是递归定义的，所以只需要寻找根节点、左子树以及右子树之间的关系，即可构造出二叉树。

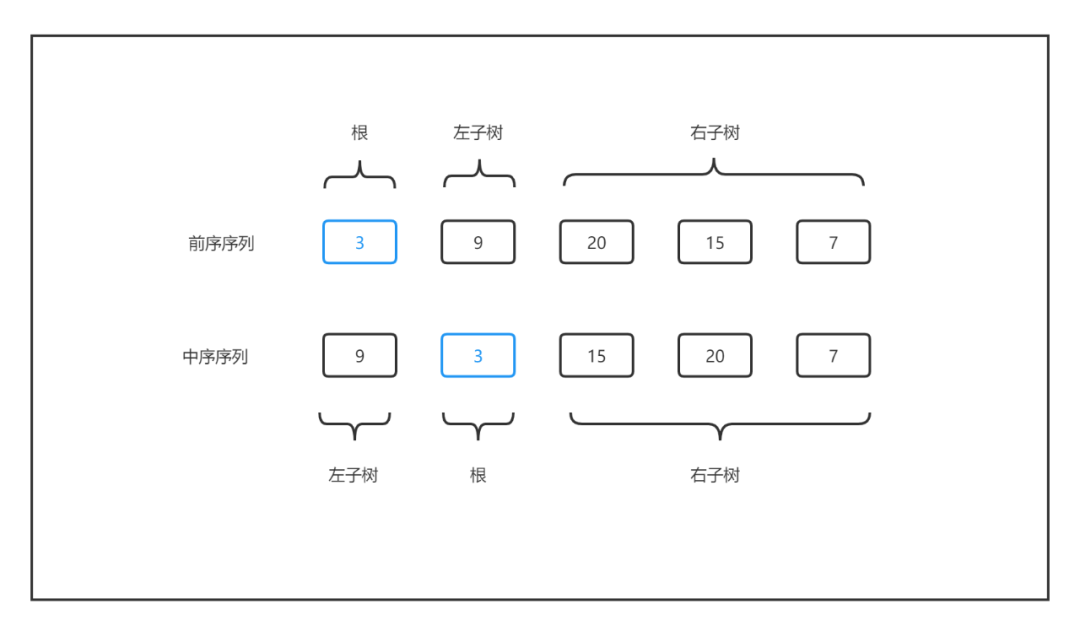
  参照上述图解，通过前序序列可以轻松地找到当前子树的根节点，然后通过中序序列依据该根节点分割其左右子树，所以这里有一个重要的隐藏条件就是二叉树中的元素值不能重复！

  时间复杂度：O(n)，空间复杂度：O(n)。

const buildTree = (preorder, inorder) => {// 递归中止条件if (preorder.length === 0) {return null;}const rootElement = preorder[0];const root = new TreeNode(rootElement);const rootElementIndex = inorder.indexOf(rootElement);root.left = buildTree(preorder.slice(1, rootElementIndex + 1), inorder.slice(0, rootElementIndex));root.right = buildTree(preorder.slice(rootElementIndex + 1), inorder.slice(rootElementIndex + 1));return root;
}

  针对上述解法中的 indexOf 耗时，可以通过空间换时间的技巧来优化。

  利用哈希表将中序序列中各个根节点的映射关系提前保存好，但是这样会面临一个新的问题？就是不能再对 inorder 进行 slice，这样会导致映射关系发生变化。这里就需要转化为利用下标来维护两个序列的区间。

  而计算下标其中一个重要的点就是计算出左右子树的长度，这个仍然是利用前序序列和中序序列的特性来解决。

  另一个值得注意的点就是递归条件的变化。

  时间复杂度：O(n)，空间复杂度：O(n)。

const buildTree = (preorder, inorder) => {const record = new Map();for (let i = 0; i < inorder.length; i++) {record.set(inorder[i], i);}const _buildTree = (start1, end1, start2, end2) => {// 递归中止条件if (start1 > end1) {return null;}const element = preorder[start1];const root = new TreeNode(element);const index = record.get(element);const rightTreeLength = end2 - index;const leftTreeLength = end1 - start1 - rightTreeLength;root.left = _buildTree(start1 + 1, start1 + 1 + leftTreeLength - 1, index - leftTreeLength, index - 1);root.right = _buildTree(start1 + leftTreeLength + 1, end1, index + 1, end2);return root;}return _buildTree(0, preorder.length - 1, 0, inorder.length - 1);
}

106. 从中序与后序遍历序列构造二叉树

  「题目：」

  给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这棵 二叉树 。

  「示例：」

  输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]，输出：[3,9,20,null,null,15,7]。

  「解题思路：」

  本道题的后序序列发挥着与前道题中的前序序列一样的作用，也是在后序序列中寻找根节点的位置，然后再根据根节点的位置，在中序序列中分割出左右子树。

  时间复杂度：O(n)，空间复杂度：O(n)。

const buildTree = (inorder, postorder) => {if (inorder.length === 0) {return null;}const el = postorder.pop();const root = new TreeNode(el);const index = inorder.indexOf(el);root.left = buildTree(inorder.slice(0, index), postorder.slice(0, index));root.right = buildTree(inorder.slice(index + 1), postorder.slice(index));return root;
}

  至于优化解法，有兴趣的同学可以参考前道题的思路。

889. 根据前序和后序遍历构造二叉树

  「题目：」

  给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

  如果存在多个答案，您可以返回其中 任何 一个。

  「示例：」

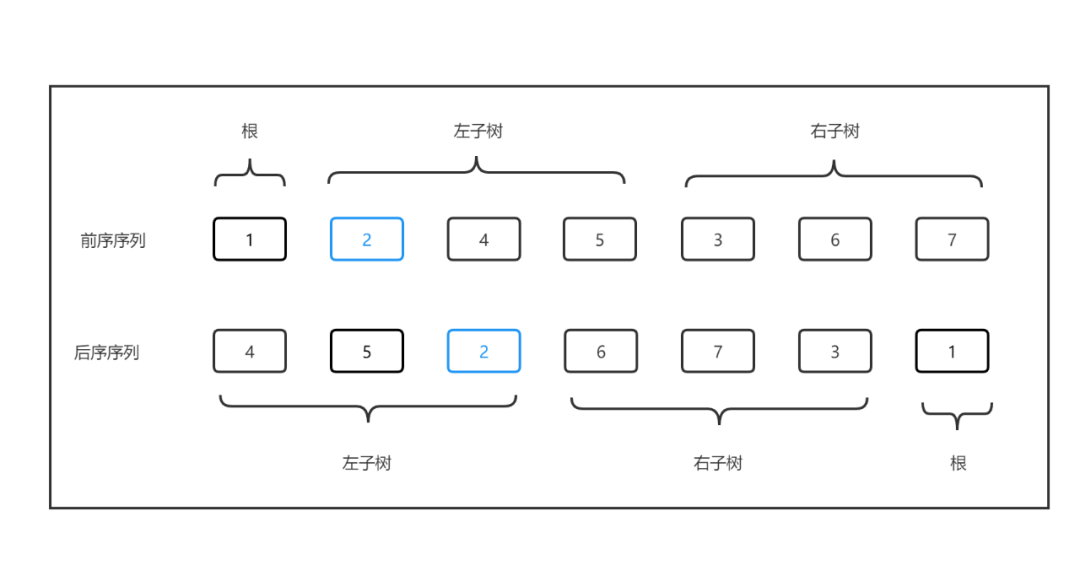
  输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]，输出：[1,2,3,4,5,6,7]。

  「解题思路：」

  前序序列和后序序列都可以很容易地定位到根节点，但是两个序列同时出现的时候，无法直接分割出左右子树。

  根据前序序列的特性，其序列的第一个元素是当前二叉树的根节点，那么其第二个元素就是左子树的根节点，根据该节点又可以在后序序列中分割出左右子树。

  时间复杂度：O(n)，空间复杂度：O(n)。

const constructFromPrePost = (pre, post) => {if (pre.length === 0) {return null}// 拿出根节点const rootValue = pre.shift()post.pop()const root = new TreeNode(rootValue)if (pre.length > 0) {// 左子树的根节点const l = pre[0]const lIndex = post.indexOf(l)root.left = constructFromPrePost(pre.slice(0, lIndex + 1), post.slice(0, lIndex + 1))root.right = constructFromPrePost(pre.slice(lIndex + 1), post.slice(lIndex + 1))}return root
}

1008. 前序遍历构造二叉搜索树

  「题型：」

  给定一个整数数组，它表示BST(即 二叉搜索树 )的 先序遍历 ，构造树并返回其根。

  保证 对于给定的测试用例，总是有可能找到具有给定需求的二叉搜索树。

  「示例：」

  输入：preorder = [8,5,1,7,10,12]，输出：[8,5,10,1,7,null,12]。

  「第一种解题思路：」

  由于 BST 的中序序列是一个升序序列，那么可以通过对前序序列排序得到其中序序列，从而将本题转化为【105. 从前序与中序遍历序列构造二叉树】。

  时间复杂度：O(n)，空间复杂度：O(n)。

const bstFromPreorder = (preorder) => {const inorder = preorder.map(item => item).sort((a, b) => a - b);return buildTree(preorder, inorder);
}const buildTree = (preorder, inorder) => {if (preorder.length === 0) {return null;}const rootValue = preorder.shift();const root = new TreeNode(rootValue);const index = inorder.indexOf(rootValue);root.left = buildTree(preorder.slice(0, index), inorder.slice(0, index));root.right = buildTree(preorder.slice(index), inorder.slice(index + 1));return root;
}

  「第二种解题思路：」

  利用 BST 的根元素严格大于其左子树的所有节点的特性，从而分割出左右子树。

  时间复杂度：O(n)，空间复杂度：O(n)。

const bstFromPreorder = preorder => {// 终止条件if (!preorder.length) {return null}const root = new TreeNode(preorder[0])// 寻找左右子树的分割点let index = 0const max = preorder.lengthfor (let i = 0; i < max; i++) {if (preorder[0] >= preorder[i]) {index = icontinue}break}root.left = bstFromPreorder(preorder.slice(1, index + 1))  root.right = bstFromPreorder(preorder.slice(index + 1))return root
}

写在最后

  「感谢您能耐心地读到这里，如果本文对您有帮助，欢迎点赞、分享、或者关注下方的公众号哟。」

  相关链接：

• https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

• https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

• https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-postorder-traversal/

• https://leetcode.cn/problems/construct-binary-search-tree-from-preorder-traversal/

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！