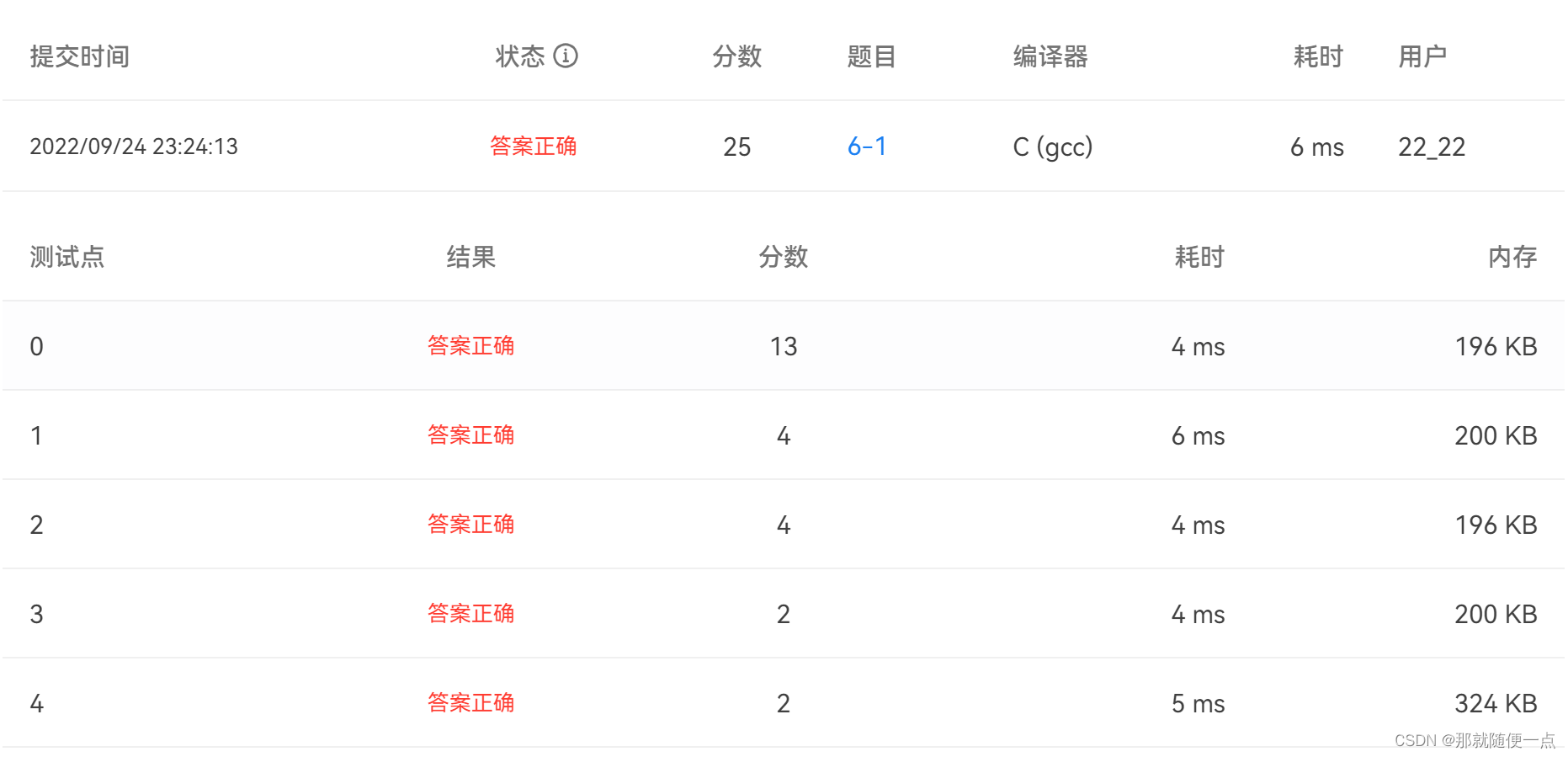
6-1 二叉树的非递归遍历

 

本题要求用非递归的方法实现对给定二叉树的 3 种遍历。

函数接口定义：

void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );

其中BinTree结构定义如下：

typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;int flag;
};

要求 3 个函数分别按照访问顺序打印出结点的内容，格式为一个空格跟着一个字符。

此外，裁判程序中给出了堆栈的全套操作，可以直接调用。

裁判测试程序样例：

#include 
#include 
typedef enum { false, true } bool;typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;int flag;
};/*------堆栈的定义-------*/
typedef Position SElementType;
typedef struct SNode *PtrToSNode;
struct SNode {SElementType Data;PtrToSNode Next;
};
typedef PtrToSNode Stack;/* 裁判实现，细节不表 */
Stack CreateStack();
bool IsEmpty( Stack S );
bool Push( Stack S, SElementType X );
SElementType Pop( Stack S ); /* 删除并仅返回S的栈顶元素 */
SElementType Peek( Stack S );/* 仅返回S的栈顶元素 */
/*----堆栈的定义结束-----*/BinTree CreateBinTree(); /* 裁判实现，细节不表 */
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );int main()
{BinTree BT = CreateBinTree();printf("Inorder:");    InorderTraversal(BT);    printf("\n");printf("Preorder:");   PreorderTraversal(BT);   printf("\n");printf("Postorder:");  PostorderTraversal(BT);  printf("\n");return 0;
}
/* 你的代码将被嵌在这里 */

输入样例：

如图

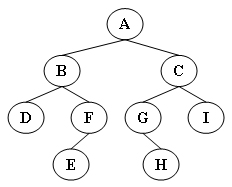
输出样例：

Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

 Code:

//中序遍历（左根右）非递归：(借助栈实现)
void InorderTraversal( BinTree BT ){BinTree T = BT;Stack S = CreateStack();//创建堆栈while (T || !IsEmpty(S)){//当树不空或者堆栈不空时while (T){//一直访问左子树Push(S,T);//入栈T = T -> Left;//更新 }if (!IsEmpty(S)){//左子树遍历完后，当堆栈不空时 T = Pop(S);//出栈cout << " " << T -> Data;//访问数据T = T->Right;//转为访问右子树}}
}//先序（根左右）非递归遍历：(借助栈实现)
void PreorderTraversal( BinTree BT ){BinTree T = BT;Stack S = CreateStack();//创建堆栈while (T || !IsEmpty(S)){//当树不空或者堆栈不空时while (T){//一直访问左子树Push(S,T);//入栈cout << " " << T -> Data;//访问数据T = T -> Left;//更新 }if (!IsEmpty(S)){//左子树遍历完后，当堆栈不空时 T = Pop(S);//出栈T = T -> Right;//转为访问右子树}}
}//后序（左右根）非递归遍历：(借助栈实现)
//标记入栈次数实现后序遍历
void PostorderTraversal( BinTree BT ){BinTree T = BT;Stack S = CreateStack();//创建堆栈while (T || !IsEmpty(S)){//当树不空或者堆栈不空时while (T){//一直访问左子树Push(S,T);//入栈T -> flag = 1;//记录第一次入栈T = T->Left;}if (!IsEmpty(S)){//左子树遍历完后T = Pop(S);//出栈if(T->flag == 1){//如果第一次入栈,右节点入栈Push(S,T);//入栈T->flag = 2;//意味两次入栈T = T->Right;//转为访问右子树}else{//如果第二次入栈cout << " " << T->Data;//访问数据T = NULL;}}}
}

 （如果限制C语言只需修改cin，cout即可）

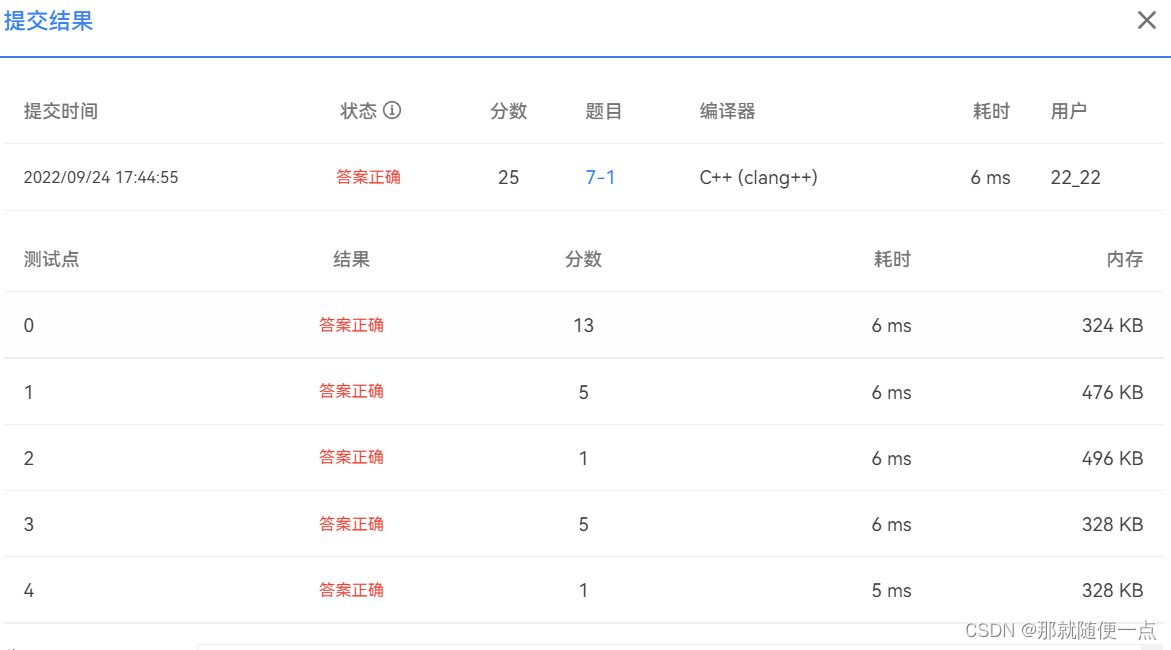
7-1 列出叶结点

对于给定的二叉树，本题要求你按从上到下、从左到右的顺序输出其所有叶节点。

输入格式：

首先第一行给出一个正整数 N（≤10），为树中结点总数。树中的结点从 0 到 N−1 编号。随后 N 行，每行给出一个对应结点左右孩子的编号。如果某个孩子不存在，则在对应位置给出 "-"。编号间以 1 个空格分隔。

输出格式：

在一行中按规定顺序输出叶节点的编号。编号间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6

输出样例：

4 1 5

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

Code:

//宽搜进行层序遍历。 
#include
using namespace std;
const int N = 100;//结构体储存左右孩子。 
struct node{int leaf ;int right;
}q[N]; queue qu; 
int res[N],tot = 0;
void bfs(){while(qu.size()){//队列不为空 int num = qu.front();//取队首 qu.pop();//出队 if(q[num].leaf == -1 && q[num].right == -1) res[tot++] = num;//是叶节点就顺序记录//不是叶节点就入队 if(q[num].leaf != -1) qu.push(q[num].leaf);if(q[num].right != -1) qu.push(q[num].right);}
}
int main(){//std::ios::sync_with_stdio(false);加速器害死人 int n,root;cin >> n;getchar();//!!!!!int flag[n];//判断根节点 char a,b;//千万别忘记转化字符为数字 //赋值为0 memset(q,0,sizeof(q));memset(flag,0,sizeof(flag));for(int i = 0;i < n;i ++ ){scanf("%c %c",&a,&b);  getchar();if(a == '-') q[i].leaf = -1;//没左孩子//有左孩子 else {q[i].leaf = a-'0';flag[q[i].leaf] = 1;} if(b == '-') q[i].right=-1;//没右孩子//有右孩子  else {q[i].right = b-'0';flag[q[i].right] = 1;} 	}//寻找根节点 for(int i = 0;i < n;i ++ ){if(flag[i] == 0){root = i;break;}}//读入根节点 qu.push(root);//宽搜 bfs();//第一个没有空格。 cout << res[0];//按顺序输出叶节点（数组已经储存好顺序了） for(int i = 1;i < tot;i ++ ){cout << " " << res[i];}return 0;
}

备注：既没有左孩子又没有右孩子的才是叶结点。

7-2 完全二叉搜索树

一个无重复的非负整数序列，必定对应唯一的一棵形状为完全二叉树的二叉搜索树。本题就要求你输出这棵树的层序遍历序列。

输入格式：

首先第一行给出一个正整数 N（≤1000），随后第二行给出 N 个不重复的非负整数。数字间以空格分隔，所有数字不超过 2000。

输出格式：

在一行中输出这棵树的层序遍历序列。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

10
1 2 3 4 5 6 7 8 9 0

输出样例：

6 3 8 1 5 7 9 0 2 4

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

 Code:

//二叉搜索树的层次遍历对应完全二叉树的中序遍历#include
using namespace std;
const int N = 1e3 + 10;int res[N];
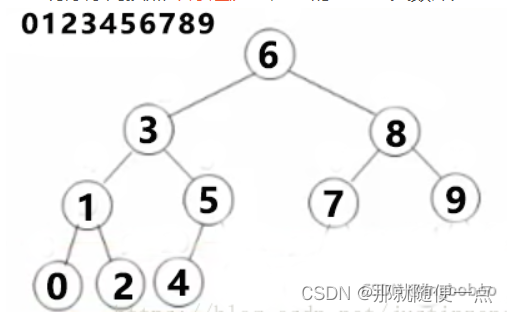
int tem[N];//位置下标数组int n,cnt = 0;//先依据完美二叉树的层序遍历建立一颗标准树（只有通过标准树的位置的对应才能实现对于二叉搜索树层序遍历的输出），再中序访问（左中右）建立按照中序访问顺序的位置对应层序遍历的位置（如图中0位于标准树的第8号位置）
void dfs(int x){//终结条件if(x > n) return ;dfs(2 * x);tem[x] = ++ cnt;dfs(2 * x + 1);
} int main(){cin >> n;for(int i = 1;i<=n;i++){cin >> res[i];}//排序 sort(res + 1,res + 1 + n);//开始递归建立树 dfs(1);//输出 for(int i = 1;i <= n;i ++ ){//注意格式//依据对应关系输出if(i == 1)cout << res[tem[i]];elsecout << " " << res[tem[i]];}return 0;
}

7-3 根据后序和中序遍历输出先序遍历

本题要求根据给定的一棵二叉树的后序遍历和中序遍历结果，输出该树的先序遍历结果。

输入格式:

第一行给出正整数N(≤30)，是树中结点的个数。随后两行，每行给出N个整数，分别对应后序遍历和中序遍历结果，数字间以空格分隔。题目保证输入正确对应一棵二叉树。

输出格式:

在一行中输出Preorder: 以及该树的先序遍历结果。数字间有1个空格，行末不得有多余空格。

输入样例:

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例:

Preorder: 4 1 3 2 6 5 7

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

Code:

#include 
using namespace std;
const int N = 1e2 + 10;
int pre[N]{0}, in[N]{0}, post[N]{0};
void dfs(int preL, int inL, int postL, int n){if(n == 0) return;else if(n == 1) {pre[preL] = post[postL];  return;}int root = post[postL + n - 1]; //后序序列的最后一个节点是根pre[preL] = root;               //先序遍历的第一个节点是根节点int  i;for(i = 0; i < n; i++)if(in[inL + i] == root)     //找到根节点在中序遍历的位置break;int L = i, R = n - L - 1;       //L表示左子树的节点个数, R表示右子树的节点个数dfs(preL + 1, inL, postL, L); //递归完成左子树的先序序列dfs(preL + 1 + L, inL + L + 1, postL + L, R);//递归完成右子树的先序序列
}int main(){int n;cin >> n;for(int i = 0; i < n; i ++ ) cin >> post[i];for(int i = 0; i < n; i ++ ) cin >> in[i]; dfs(0, 0, 0, n);cout << "Preorder: ";//格式控制cout << pre[0];for(int i = 1; i < n; i++) cout << " " << pre[i];return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！