[Python] 使用约登指数寻找最佳ROC曲线阈值

[预备知识]

对于二元分类结果评价，ROC曲线是常用标准，其使用TPR与FPR绘制而成。(相关知识推荐博文：一文让你彻底理解准确率，精准率，召回率，真正率，假正率，ROC/AUC) 而TPR与FPR的计算是根据选定的一系列阈值(Threshold)得到的，本文的目的便是寻找最优阈值，在假正率FPR与真正率TPR之间做折中。ROC用以判断分类模型好坏，是否足以区分两类对象，而寻找最佳阈值可以使分类效果达到最优，符合实际应用要求。

[计算方法]

Youden Index

参考链接：全面了解ROC曲线

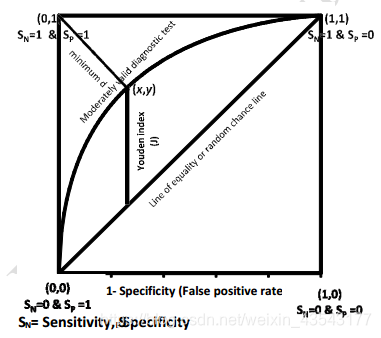
如图所示，该方法的思想是找到横坐标 $1-Specificity$ 与 纵坐标 $Sensitivity$ 差异最大的点所对应的阈值。在本文中描述为：
$$index=argmax(TPR-FPR),$$
最终可以得到最优阈值及其ROC曲线坐标：
t h o p t i m a l = t h r e s h o l d s [ i n d e x ] th_{optimal}=thresholds[index] thoptimal​=thresholds[index]

p o i n t o p t i m a l = ( F P R [ i n d e x ] , T P R [ i n d e x ] ) point_{optimal}=(FPR[index], TPR[index]) pointoptimal​=(FPR[index],TPR[index])
很简单吧！

Codes using Python

def Find_Optimal_Cutoff(TPR, FPR, threshold):"""threshold 一般通过sklearn.metrics里面的roc_curve得到，具体不赘述，可以参考其他资料。:param threshold: array, shape = [n_thresholds]"""y = TPR - FPRYouden_index = np.argmax(y)  # Only the first occurrence is returned.optimal_threshold = threshold[Youden_index]point = [FPR[Youden_index], TPR[Youden_index]]return optimal_threshold, point

ROC的计算及绘制也放一下：

def ROC(label, y_prob):"""Receiver_Operating_Characteristic, ROC:param label: (n, ):param y_prob: (n, ):return: fpr, tpr, roc_auc, optimal_th, optimal_point"""fpr, tpr, thresholds = metrics.roc_curve(label, y_prob)roc_auc = metrics.auc(fpr, tpr)optimal_th, optimal_point = Find_Optimal_Cutoff(TPR=tpr, FPR=fpr, threshold=thresholds)return fpr, tpr, roc_auc, optimal_th, optimal_point

fpr, tpr, roc_auc, optimal_th, optimal_point = ROC(labels, img_distance)plt.figure(1)
plt.plot(fpr, tpr, label=f"AUC = {roc_auc:.3f}")
plt.plot([0, 1], [0, 1], linestyle="--")
plt.plot(optimal_point[0], optimal_point[1], marker='o', color='r')
plt.text(optimal_point[0], optimal_point[1], f'Threshold:{optimal_th:.2f}')
plt.title("ROC-AUC")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.legend()
plt.show()

[结果]

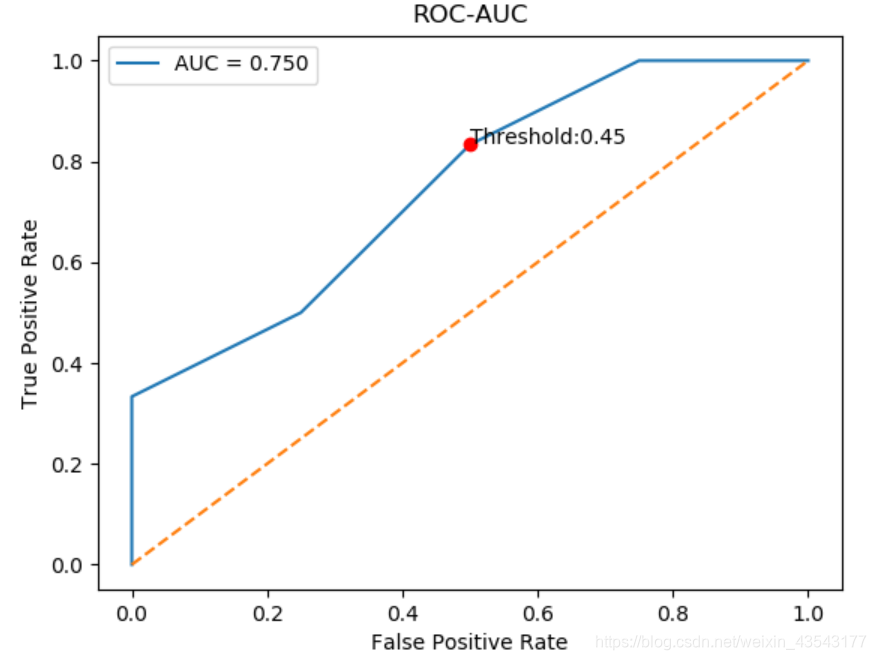
红色的点即为最佳阈值啦，完结撒花。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！