【卡尔曼滤波】基于多模型卡尔曼滤波检测多用户噪声无线系统中的信号研究(Matlab代码实现)
👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
本文基于多模型卡尔曼滤波检测多用户噪声无线系统中的信号研究。
📚2 运行结果
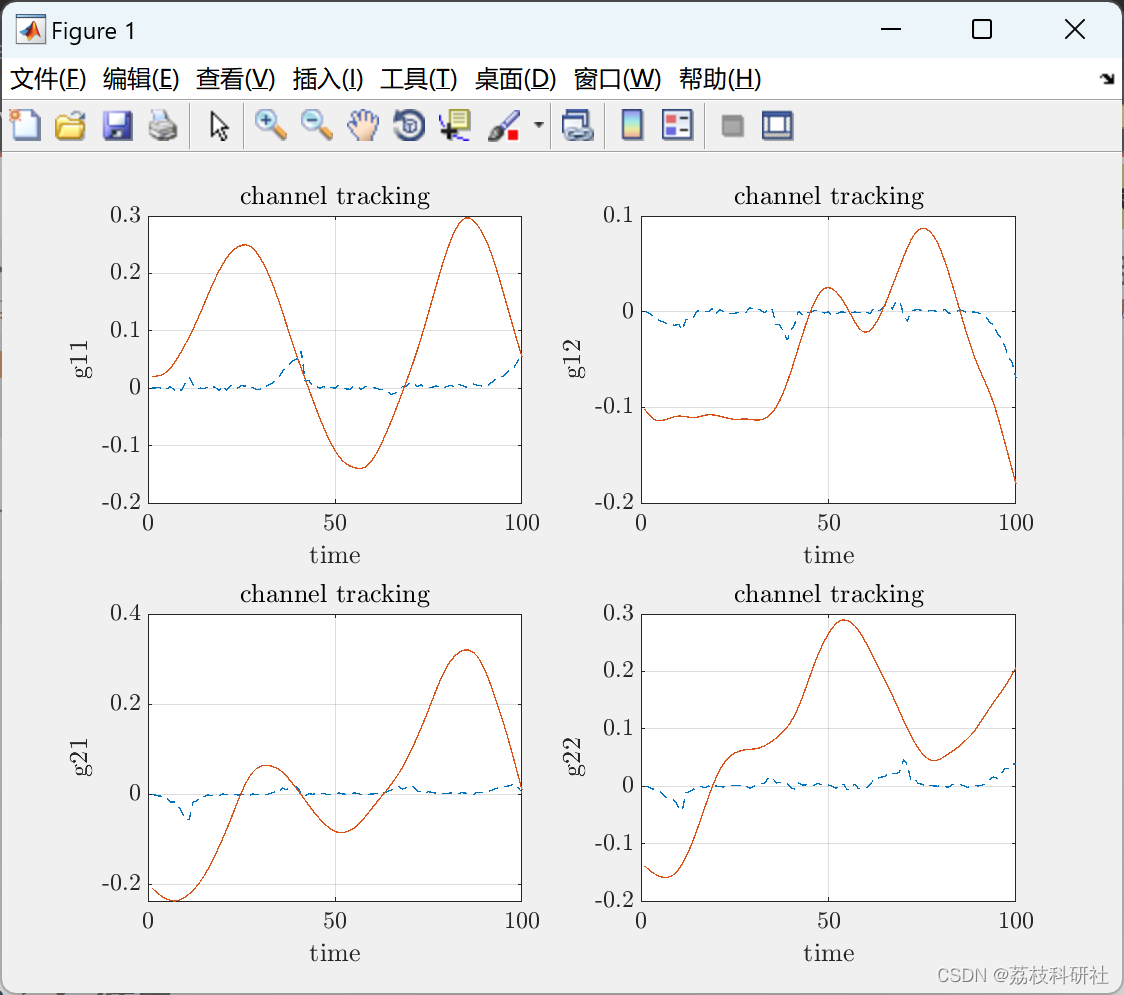
部分代码:
%Kalman Filter for user k matched to symbol 1
j=4;
B((k-1)*4+1:4*k,(k-1)*4+1:4*k) = blkdiag(sym(j,1)*eye(2), sym(j,2)*eye(2));
xp1 = xh0m(:,j);
Pp1 = Ph0m(:,:,j) + Q;
C(:,:,j) = LT * A * B;
H = C((k-1)*4+1:4*k,(k-1)*4+1:4*k,j);
if k ~= 1
H1= C((k-1)*4+1:4*k,1:(k-1)*4,j);
xp3 = (H1 * xp2);
V1 = H1*P*ctranspose(H1);
end;
[xh4(:,k),Ph4(:,:,k),Rlike(j)]=kalman(y1((k-1)*4+1:k*4,t),H,xp1,xp3,V,V2,V1,Pp1);
Rlike=real(Rlike);
Rsumlike=sum(Rlike);
if (Rsumlike~=0),
Rlike=Rlike/Rsumlike;
end;
like=Rlike;
if(like==0),
like
pause;
end;
% like=real(like);
%Calculation of mode probabilities
for j=1:M,
modePr(j,k,2)= like(j) * ( Tr(1,j)* modePr(1,k,1) + Tr(2,j)* modePr(2,k,1) + Tr(3,j)* modePr(3,k,1) + Tr(4,j)* modePr(4,k,1) ); %posterior probabilities
end;
summode=sum(modePr(:,k,2));
modePr(:,k,2)=modePr(:,k,2)/summode;
[a,bk] = max(modePr(:,k,2));
mode = zeros(4,1);
mode(bk,1) = 1;
if (isnan(modePr(:,k,2))~=0)
modePr(:,k,2)
pause;
end;
%hard cancellation
temp = [xh1(:,k) xh2(:,k) xh3(:,k) xh4(:,k) ];
%hard cancellation
B((k-1)*4+1:k*4,(k-1)*4+1:k*4)=blkdiag(sym(bk,1)*eye(2),sym(bk,2)*eye(2));
xp2((k-1)*4+1:k*4,1) = temp(:,bk);
temp = [Ph1(:,:,k) Ph2(:,:,k) Ph3(:,:,k) Ph4(:,:,k) ];
P((k-1)*4*L+1:k*4*L,(k-1)*4*L+1:k*4*L) = temp(:,(bk-1)*4*L+1:bk*4*L);
end;
Rchmse(1:4,(t-1)*2+1) = Rchmse(1:4,(t-1)*2+1) + conj(abs(real(xp2(1:4,1))) - abs(real(g(1:4,(t-1)*2+1+400)))) .* (abs(real(xp2(1:4,1))) - abs(real(g(1:4,(t-1)*2+1+400))));
Ichmse(1:4,(t-1)*2+1) = Ichmse(1:4,(t-1)*2+1) + conj(abs(imag(xp2(1:4,1))) - abs(imag(g(1:4,(t-1)*2+1+400)))) .* (abs(imag(xp2(1:4,1))) - abs(imag(g(1:4,(t-1)*2+1+400))));
ghat(1:4,(t-1)*2+1) = xp2(1:4,1);
%FOR TIME i
B = zeros(K*4, K*4);
xp1 = zeros(4, 1);
Pp1 = zeros(4, 4);
xp2 = zeros(0,1);
xp3 = zeros(4,1);
Pp2 = zeros(4, 4);
P = zeros(0, 0);
V1 = zeros(4,4);
V2 = zeros(4,4);
H1 = zeros(0, 0);
for k=1:K,
Tr = [0 0 1 0; 1 0 0 0; 0 0 0 1; 0 1 0 0]; %for next time instant all possible transitions are known
% Tr = [0.00001 0.00001 0.99997 0.00001; 0.99997 0.00001 0.00001 0.00001; 0.00001 0.00001 0.00001 0.99997; 0.00001 0.99997 0.00001 0.00001]; %for next time instant all possible transitions are known
%calculation of mixing probabilities
for i=1:M,
for j=1:M,
mu(i,j) = Tr(i,j)*modePr(i,k,2); %prior probabilities, mode prob is from the previous time instant in ST matrix
end;
end;
%MIXING
for j=1:M,
xh0m(:,j) = xh1(:,k)*mu(1,j) + xh2(:,k)*mu(2,j) + xh3(:,k)*mu(3,j) + xh4(:,k)*mu(4,j);
Ph0m(:,:,j)= mu(1,j)*(Ph1(:,:,k) + (xh1(:,k) - xh0m(:,j))*ctranspose(xh1(:,k)-xh0m(:,j)) ) + mu(2,j)*(Ph2(:,:,k) + (xh2(:,k)-xh0m(:,j))*ctranspose(xh2(:,k)-xh0m(:,j))) + mu(3,j)*(Ph3(:,:,k) + (xh3(:,k) - xh0m(:,j))*ctranspose(xh3(:,k)-xh0m(:,j)) ) + mu(4,j)*(Ph4(:,:,k) + (xh4(:,k)-xh0m(:,j))*ctranspose(xh4(:,k)-xh0m(:,j)));
end;
%Mode matched filtering
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]史飞,牛慧莹,王济,吕鹏.一种采用卡尔曼滤波与正则匹配的信号盲检测法[J].无线电通信技术,2023,49(01):182-186.
🌈4 Matlab代码实现
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!
