python 如何计算差分

一、p阶k步差分定义说明

n阶差分

▽ x t \triangledown x_t ▽xt​为 x t x_t xt​的1阶差分： ▽ x t = x t − x t − 1 \triangledown x_t=x_t-x_{t-1} ▽xt​=xt​−xt−1​
▽ 2 x t \triangledown^2 x_t ▽2xt​为 x t x_t xt​的2阶差分： ▽ x t = ▽ x t − ▽ x t − 1 \triangledown x_t=\triangledown x_t-\triangledown x_{t-1} ▽xt​=▽xt​−▽xt−1​
▽ n x t \triangledown^n x_t ▽nxt​为 x t x_t xt​的n阶差分： ▽ x t = ▽ n − 1 x t − ▽ n − 1 x t − 1 \triangledown x_t=\triangledown^{n-1} x_t-\triangledown^{n-1} x_{t-1} ▽xt​=▽n−1xt​−▽n−1xt−1​

k步差分

▽ k x t \triangledown_k x_t ▽k​xt​为 x t x_t xt​的1阶差分： ▽ k x t = x t − x t − k \triangledown_k x_t=x_t-x_{t-k} ▽k​xt​=xt​−xt−k​

二、python实现

1. n阶差分

diff_p = diff(data, n=n) #默认k=1

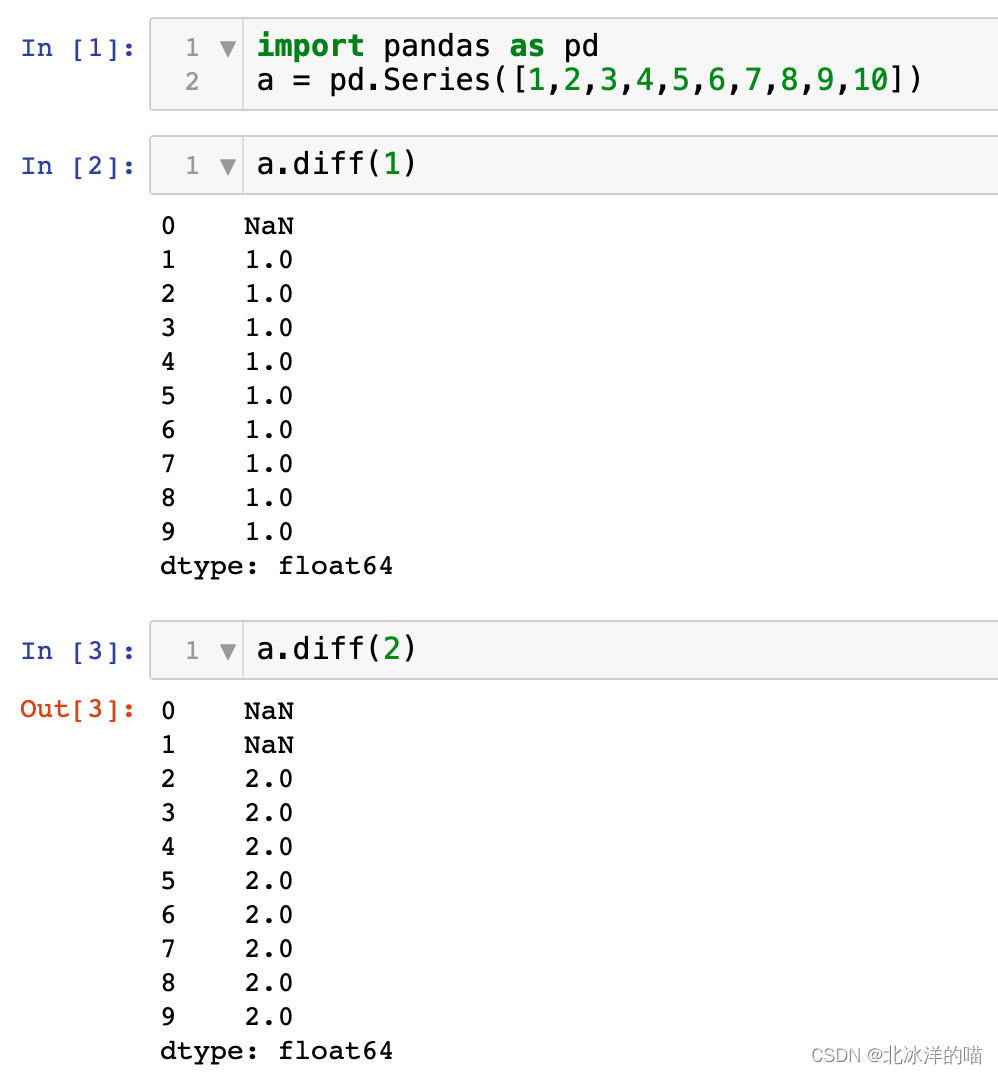
2. k步差分

diff_k_step = data.diff(k)

3. n阶k步差分

import numpy as np# 定义一个长度为 10 的数组 x
x = pd.Series([1, 3, 6, 10, 15, 21, 28, 36, 45, 55])
n=2
k=3
for i in range(n):x = x.diff(k)
y = xprint(y)

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！