Density-based Clustering

Density-based Clustering

密度聚类即"“基于密度的聚类”，它基于这样一个假设：聚类结构能通过样本分布的紧密程度确定。

Mean-Shift

K-means算法的效果受到聚类中心初始点的选择以及$K$值的设置，当面对于簇个数未知的数据，以及数据流形的形状不规则时，k-means以及相应的改进算法就难以取得理想的效果。

均值移动聚类算法：它是一种滑动窗口类型的算法，帮助找到密集区域的数据点，同时也是一种基于形心的算法，目标是定位每个簇的中心点。其工作原理是更新候选中心点作为滑动窗口内点的平均值，后处理阶段是过滤候选窗口进行消重，从而形成最后一个簇中心点及其对应的簇。

假设给定$d$维空间中的$n$个数据点记为 x i , i = 1 , 2 , . . . , n x_{i},i=1,2,...,n xi​,i=1,2,...,n，对于某一个数据点 x i x_{i} xi​而言，它所对应的mean shift向量为： M h = 1 h ∑ x i ∈ S h ( x i − x ) M_{h}=\frac{1}{h}\sum_{x_{i} \in S_{h}}(x_{i}-x) Mh​=h1​xi​∈Sh​∑​(xi​−x)

如下图所示，上式中的 S h S_{h} Sh​为半径为$h$的高维球形或超球形区域， x i x_{i} xi​为球形区域中的点，$x$为形心，区域中所有的点与以形心为起点的向量相加得到mean shift向量 M h M_{h} Mh​，即下图中的黄色箭头表示的向量。

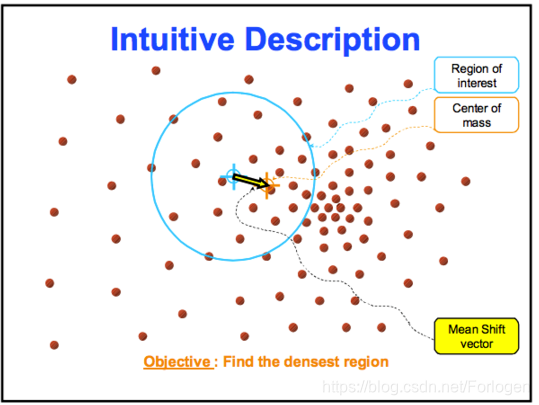
然后根据mean shift向量计算出当前的偏移值，将该点移动到偏移值对应的新的数据点处，并以此为起始点继续移动，不断迭代指导满足最终的停止条件。

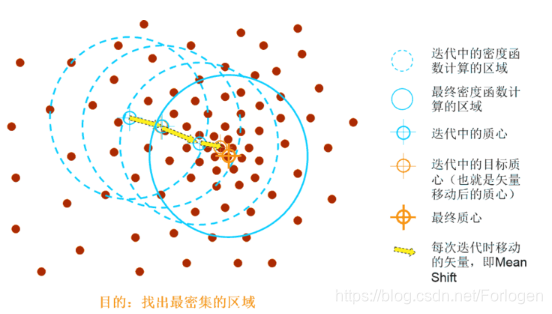
从如图所示的二维情形下的实验中可以看出，它每一步都要将起始点移动到一个密度更高的区域，直到收敛为止。而且在每次迭代中，通过将中心点更改为窗口内点的平均值，窗口会向更密集的区域移动，窗口内的点越多，滑动窗口内的密度越大。

因此，改变窗口内点的平均值意味着窗口逐渐向更密集的区域移动，继续根据平均值移动窗口，直到到达容纳其中最大点数的点为止。用多个滑动窗口重复这个过程，直到所有的点都位于一个窗口内。如果窗口有重叠的话，以点数较多的窗口为准。

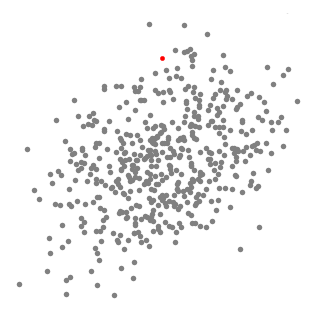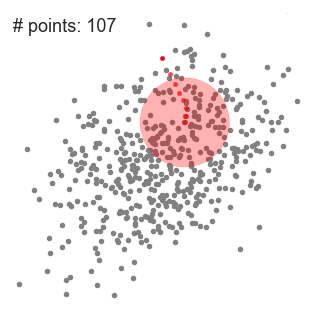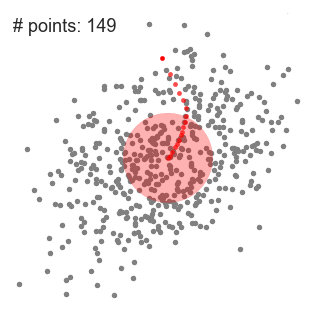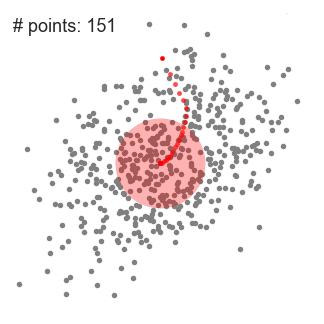
另外，为了考虑不同距离的点对于mean shift向量的贡献不同引入了核函数，核函数的值在计算过程中相当于一个权重来表示贡献程度的强弱，对应的 M h M_{h} Mh​的计算为： M h ( x ) = ∑ i = 1 n G ( x i − x h i ( x i − x ) ) ∑ i n G ( x i − x h i ) M_{h}(x)=\frac{\sum_{i=1}^n G(\frac{x_{i}-x}{h_{i}}(x_{i}-x))}{\sum_{i}^nG(\frac{x_{i}-x}{h_{i}})} Mh​(x)=∑in​G(hi​xi​−x​)∑i=1n​G(hi​xi​−x​(xi​−x))​

Mean-Shift的优点在于不需要在算法开始的时候需要确定簇的个数$K$，而是由数据驱动，簇的中心不断的向样本密度最大的点收敛。但是也需要确定窗口的大小或半径$t$，它们的选择的好坏也直接影响着最后的结果。

Mean-Shift常见的应用领域有聚类、图像分割、图像平滑、轮廓提取和目标跟踪等。

有关Mean-Shift相关的数学推导了代码解析可继续阅读：
均值偏移（ mean shift ）？
聚类算法之Mean Shift

sklearn中相应的实现类为sklearn.cluster.MeanShift，它所对应的参数为：

• bandwidth：如果选择引入核函数的版本，它用于径向基核函数（RBF）中
• seeds：用于初始化核函数
• …

sklearn提供了一个使用mean shift进行聚类的例子：

import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs# #############################################################################
# 利用make_blobs()生成一些满足高斯分布且各向同性的样本点，这里有三个中心点
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)# #############################################################################
# The following bandwidth can be automatically detected using
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)# 计算mean shift向量并进行聚类
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)print("number of estimated clusters : %d" % n_clusters_)# #############################################################################
# Plot result
import matplotlib.pyplot as plt
from itertools import cycleplt.figure(1)
plt.clf()colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):my_members = labels == kcluster_center = cluster_centers[k]plt.plot(X[my_members, 0], X[my_members, 1], col + '.')plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,markeredgecolor='k', markersize=14)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

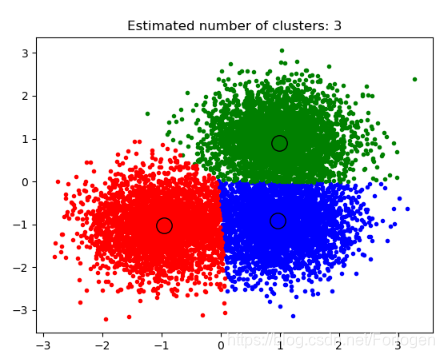
实验结果：

LVQ (Learning Vector Quantization)

具体可见之前总结的一篇博文：

学习矢量量化（Learning Vector Quantization, LVQ）

DBSCAN（ensity-Based Spatial Clustering of Applications with Noise）

DBSCAN是基于密度的聚类算法中最为经典的一个算法，它使用邻域（$ϵ,MinPts$）的概念来描述样本之间的紧密程度，其中$ϵ$表示邻域距离的阈值，MinPts表示邻域内样本点个数的阈值。算法在不断的迭代过程中将具有足够密度的区域划分为一个个的簇，且它能在有噪声点的条件下发现任意形状的簇，而不像是k-means算法那样对于数据的分布形状有一定的要求。

为了更好的理解DBCSAN的算法流程，首先我们需要明白几个其中涉及的重要概念：

• 邻域：对于任意给定的样本点$x$和$ϵ$，$x$的领域指距离$x$不超过$ϵ$的所有样本点的集合
• 核心对象：对于任意给定的样本点$x$，如果它的$ϵ$邻域内的样本点个数不少于MinPts则称其为核心对象
• 密度直达：若 x i x_{i} xi​为核心对象， x j x_{j} xj​位于 x i x_{i} xi​的$ϵ$邻域内，则称 x i x_{i} xi​可由 x j x_{j} xj​密度直达，反之不成立
• 密度可达：对于给定的样本点 x i x_i xi​和 x j x_j xj​，如果存在样本点序列 p 1 , p 2 , . . . , p T p_{1},p_{2},...,p_{T} p1​,p2​,...,pT​， p 1 = x i ， p T = x j p_{1}=x_{i}，p_{T}=x_{j} p1​=xi​，pT​=xj​，且序列中的每个样本都和它的前一个样本密度直达，则称 x i x_i xi​和 x j x_j xj​密度可达
• 密度相连：对于 x i x_i xi​和 x j x_j xj​，若存在样本点 x k x_{k} xk​使得 x k x_{k} xk​和 x i x_i xi​与 x j x_j xj​分别密度可达，则称 x i x_i xi​和 x j x_{j} xj​密度相连
• 噪声点：它不属于任何一个簇，即它从任何一个核心对象出发都是密度不可达的
  

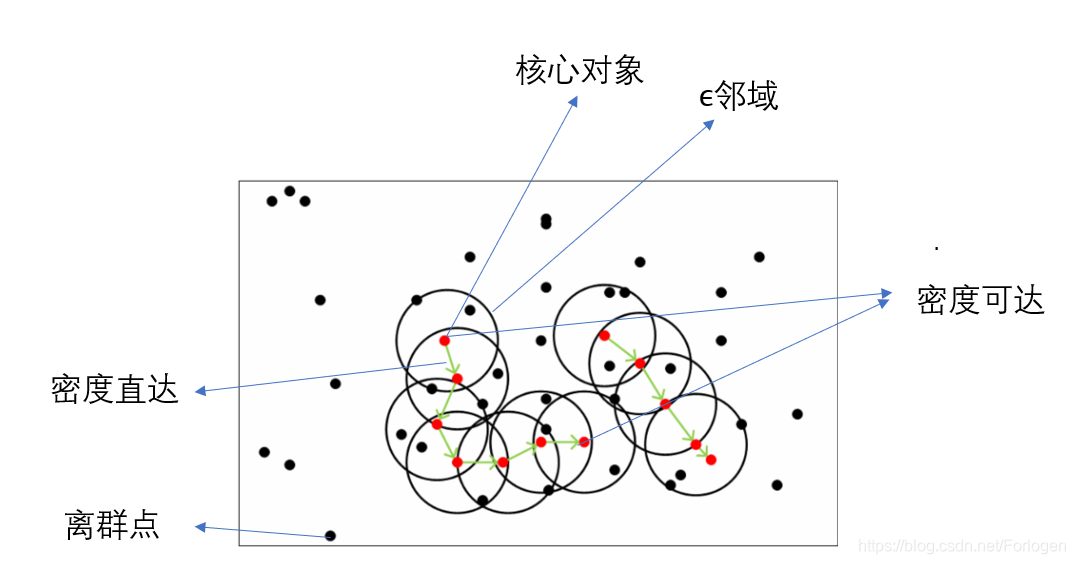
DBSCAN算法原理：由密度可达关系导出最大密度相连的样本集合。这样的一个集合中有一个或多个核心对象，如果只有一个核心对象，则簇中其他非核心对象都在这个核心对象的$ϵ$邻域内；如果是多个核心对象，那么任意一个核心对象的$ϵ$邻域内一定包含另一个核心对象（否则无法密度可达），这些核心对象以及包含在它$ϵ$邻域内的所有样本构成一个类。如上图所示的情况，左下角由七个核心对象和每个核心对象的$ϵ$邻域内的所有样本点组成一个簇；它右边则是由四个核心对象和各自的$ϵ$邻域内的所有样本点组成另一个簇。

根据DBSCAN的算法思想可以得到它的算法流程：

将数据集D中所有对象标记为未处理状态
for (D中的每个对象p) doif (p已经归入某个簇或是被标记为噪声点) thencontinueelse检查对象p的ε邻域Nε(p)if Nε(p)包含的样本点个数小于MinPts then标记p为边界点或是噪声点else标记p为核心对象并建立新簇C,并将Nε(p)中其他所有的点加入Cfor Nε(p)中尚未被处理的数据点q do检查Nε(q)，若Nε(p)中至少包含MinPts个样本点，则将Nε(q)中未归入任何一个簇的对象加入Cend forend ifend if
end if

大家可以从Visualizing DBSCAN Clustering中选择一个数据集并设定对应的参数来可视化的理解DBSCAN算法的执行过程。

此外DBSCAN还需要思考三个问题：

• 对于一些不存在任何核心对象邻域内的点如何处理？DBSCAN中我们将其标记为离群点（异常）
• 如何选择距离度量？常用的如欧式距离，在我们要确定$ϵ$邻域内的点时，必须要计算样本点到所有点之间的距离，对于样本数较少的场景，还可以应付，如果数据量特别大，一般采用KD-tree或者ball-tree来快速搜索最近邻
• 如果存在样本到两个核心对象的距离都小于ε，但这两个核心对象不属于同一个类，那么该样本属于哪一个类呢？一般DBSCAN采用先来后到的方法，样本将被标记成先聚成的类。

优点：

• 不需要指定簇的个数
• 可以发现任意形状的簇
• 擅长找到离群点
• 只需要指定两个参数

不足：

• 处理高维数据有些困难（降维）
• 合适的参数难以选择
• 数据集规模较大时收敛慢

sklearn中关于DBSCAN的实现类为sklearn.cluster.DBSCAN，其中比较重要的参数由如下几个：

• eps：即邻域的半径，默认为0.5
• min_samples：即MinPts
• metric：即距离度量的方式，可sklearn.metrics.pairwise_distances中选择，默认为欧式距离
• …

DEMO：

import numpy as npfrom sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScalerimport matplotlib.pyplot as pltcenters = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,random_state=0)
X = StandardScaler().fit_transform(X)db = DBSCAN(eps=0.3, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)print('Estimated number of clusters: %d' % n_clusters_)
print('Estimated number of noise points: %d' % n_noise_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"% metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"% metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"% metrics.silhouette_score(X, labels))# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):if k == -1:# Black used for noise.col = [0, 0, 0, 1]class_member_mask = (labels == k)xy = X[class_member_mask & core_samples_mask]plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=14)xy = X[class_member_mask & ~core_samples_mask]plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=6)plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()"""
Estimated number of clusters: 3
Estimated number of noise points: 18
Homogeneity: 0.953
Completeness: 0.883
V-measure: 0.917
Adjusted Rand Index: 0.952
Adjusted Mutual Information: 0.916
Silhouette Coefficient: 0.626
"""

实验结果：

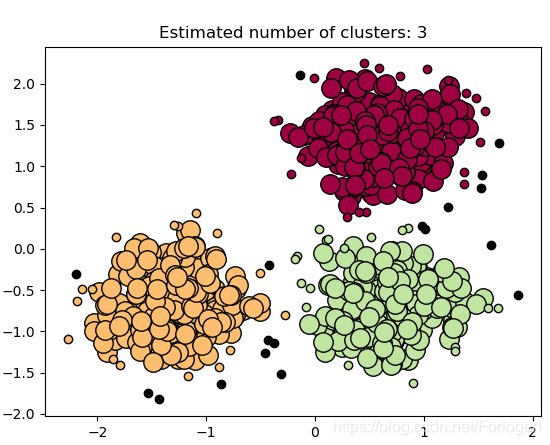
OPTICS

虽然DBSCAN效果很好且只需要设置两个参数，但是DBSCAN最终聚类的好坏对于这两个参数过于敏感。为了解决这个问题便提出了OPTICS（Ordering Points To Identify the Clustering Structure），它的改进之处主要在于对输入参数不敏感。具体来说，它并不显式的生成数据聚类而是对数据集中的样本点进行排序来得到一个有序的样本列表，其中包含了足够的信息来用于聚类。

如果对于DBSCAN算法的原理有了清晰的认识，那么理解OPTICS算法也就不难了，有兴趣的可以继续阅读以下资料。

OPTICS聚类算法
密度聚类算法之OPTICS

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！