神经网络 线性回归从0开始实现的代码分析 --跟李沐学AI

3.2. 线性回归的从零开始实现 — 动手学深度学习 2.0.0 documentation

分析了好几天才懂,个人水平有限 如果有错请指出

1.导包

%matplotlib inline
import random
import torch
from d2l import torch as d2l

def synthetic_data(w, b, num_examples):  #@save"""生成y=Xw+b+噪声"""X = torch.normal(0, 1, (num_examples, len(w)))#生成一组符合正态分布的数据(我也不是很懂正态分布的内容,但是如果随便取rang()的话数据会不稳定) 均值0平均差1   y = torch.matmul(X, w) + b #矩阵乘法 直接写X*w是不行的 不然误认为数组乘#这里由制定真实w和b根据y=Xw+b算出y y += torch.normal(0, 0.01, y.shape) #y加一组正态分布数据的误差 εreturn X, y.reshape((-1, 1))  #返回重组为n*1的列向量true_w = torch.tensor([2, -3.4]) #设出真实w和b
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)  #给出真实w和b生成X和y并赋予给features(X), labels(y)

画图那段就不分析了

迭代器部分

def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))#生成对应0-长度大小的顺序升序下标数组 0,1,2,,,,长度大小# 这些样本是随机读取的，没有特定的顺序random.shuffle(indices)#打乱数组顺序for i in range(0, num_examples, batch_size):batch_indices = np.array(indices[i: min(i + batch_size, num_examples)])#每次取10(下文设了10)个或者(数组长度-i)的长度的数据,因为是打乱的  如果是10个可能为如下            #[5,99,7,11,2,45,65,888,87,15]yield features[batch_indices], labels[batch_indices]#yield呼出迭代器,每次可以接着上次的顺序继续返回数组, 根据下面的for循环可以一次调用 一直返回直到结束 比如文中1000次就是返回100次 在for循环中  不懂得可以调试debug一下就懂了

batch_size = 10for X, y in data_iter(batch_size, features, labels):print(X, '\n', y) #输出一次试试 然后break退出break

w = np.random.normal(0, 0.01, (2, 1)) #生成一组正态分布 2x1列向量 [[w1] [w2]]
b = np.zeros(1) #[0.,]
w.attach_grad() #使参与梯度计算
b.attach_grad()

def linreg(X, w, b):  #@save"""线性回归模型"""return np.dot(X, w) + b  #点乘   返回标量

def squared_loss(y_hat, y):  #@save"""均方损失"""return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2 #经典

def sgd(params, lr, batch_size):  #@save"""小批量随机梯度下降"""for param in params:param[:] = param - lr * param.grad / batch_size #params所有参数执行一次梯度下降算法计算     除batch_size别忘了

lr = 0.03 #小的学习率
num_epochs = 3 #几个大循环
net = linreg  #线性回归作为本次网络
loss = squared_loss #平方差作为本次损失函数for epoch in range(num_epochs): #3次大循环for X, y in data_iter(batch_size, features, labels):  #每次大循环从data_iter中按batch_size个的长度大小的获取数据 with autograd.record(): l = loss(net(X, w, b), y)  # X和y的小批量损失# 计算l关于[w,b]的梯度l.backward()sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

遇到难题 看了视频还是不太懂 但是找了很多资料看懂了

1.梯度下降没能理解

定步长梯度下降算法_哔哩哔哩_bilibili

李沐那图一开始没看懂,有点懵 然后看了上面视频的23:52豁然开朗

梯度下降就是按下降速度最快的方向进行固定(可以很长可以很短)步长移动,z轴来看逐渐到达最低点的位置

下降最快的方向就是与p'切线垂直/正交,

本次实现使用学习率*梯度 ,而且梯度不断变小,到达最后逐渐逼近0,所以学习率*梯度也在慢慢变小,某一时刻点到下一时刻点的距离慢慢在缩小 

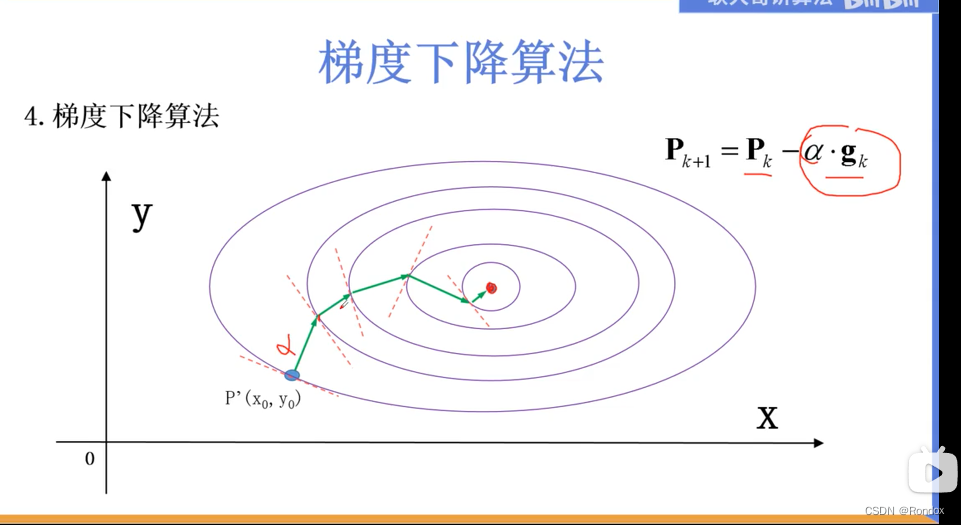
这种感觉↑

2.x.grad的问题

PyTorch：梯度计算之反向传播函数backward()_精致的螺旋线的博客-CSDN博客_pytorch backward​​​​​​​

PyTorch—backward() - 知乎

核心

 一直没搞懂x.grad是啥玩意 原来代表

下面花了计算草图

b.grad如上图结果

b_grad_a=torch.matmul(X, w)+b-y
b_grad=b_grad_a.sum() #大概是这样

调试一下观察计算过程

i=0
for epoch in range(1):for X, y in data_iter(batch_size, features, labels):#i=i+1#print(f'运行了{i}次')#for X, y in data_iter(batch_size, features, labels): 奇怪的语法 可以运行完可以遍历的内容l = loss(net(X, w, b), y)  # X和y的小批量损失# 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，# 并以此计算关于[w,b]的梯度b_grad_a=torch.matmul(X, w)+b-yb_grad=b_grad_a.sum()l.sum().backward()sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

初始b=0  取一组数据测一测

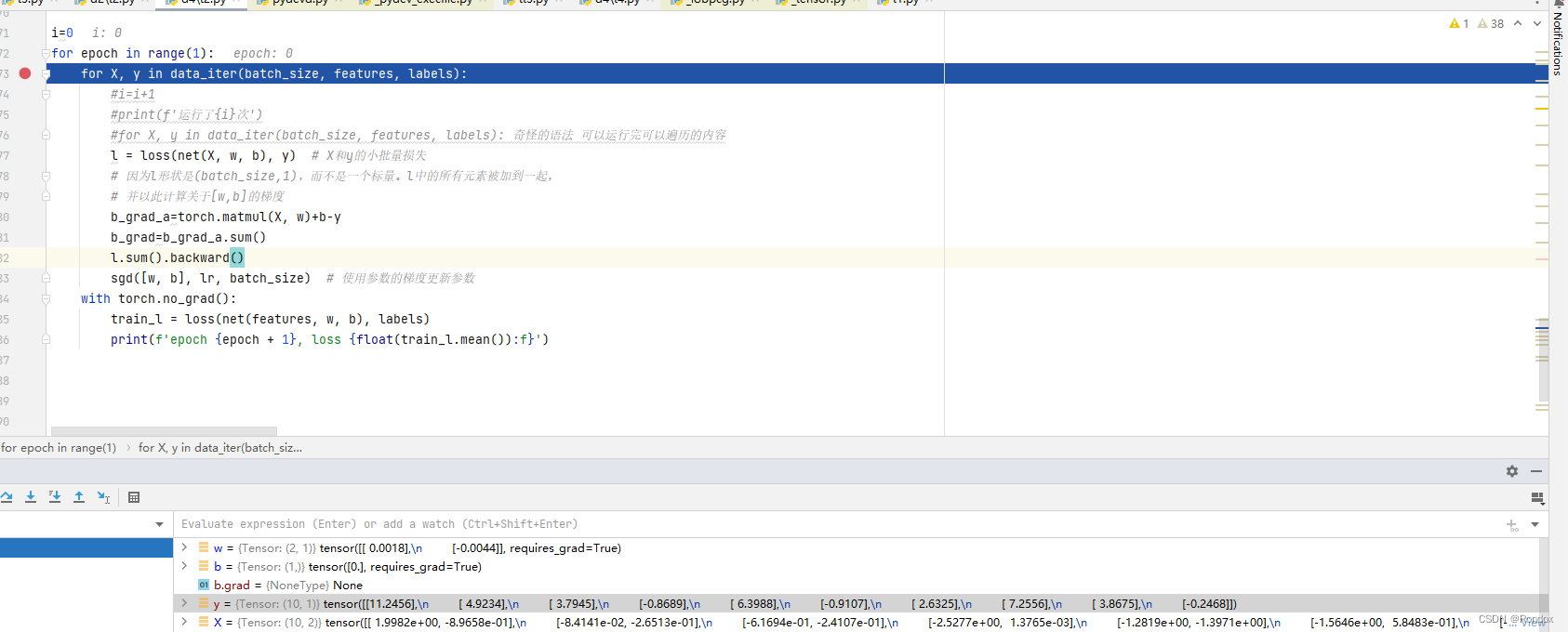
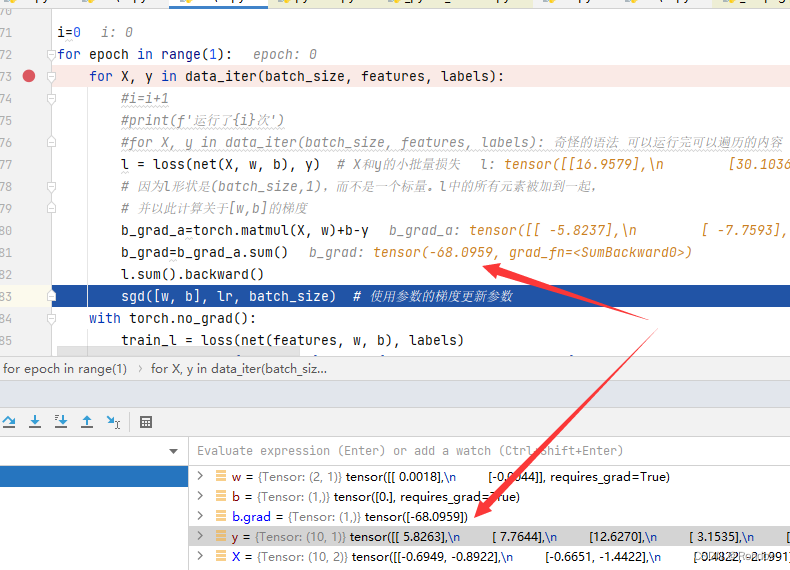 b对的

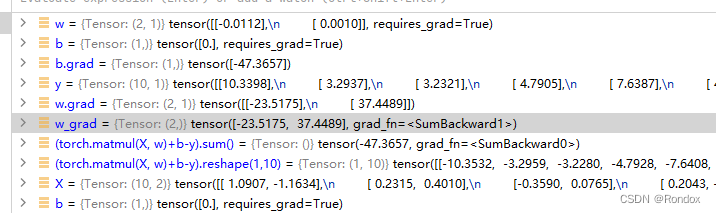
测一测w   为什么W的式子是这样的? 调了一晚上才对得上 不理解

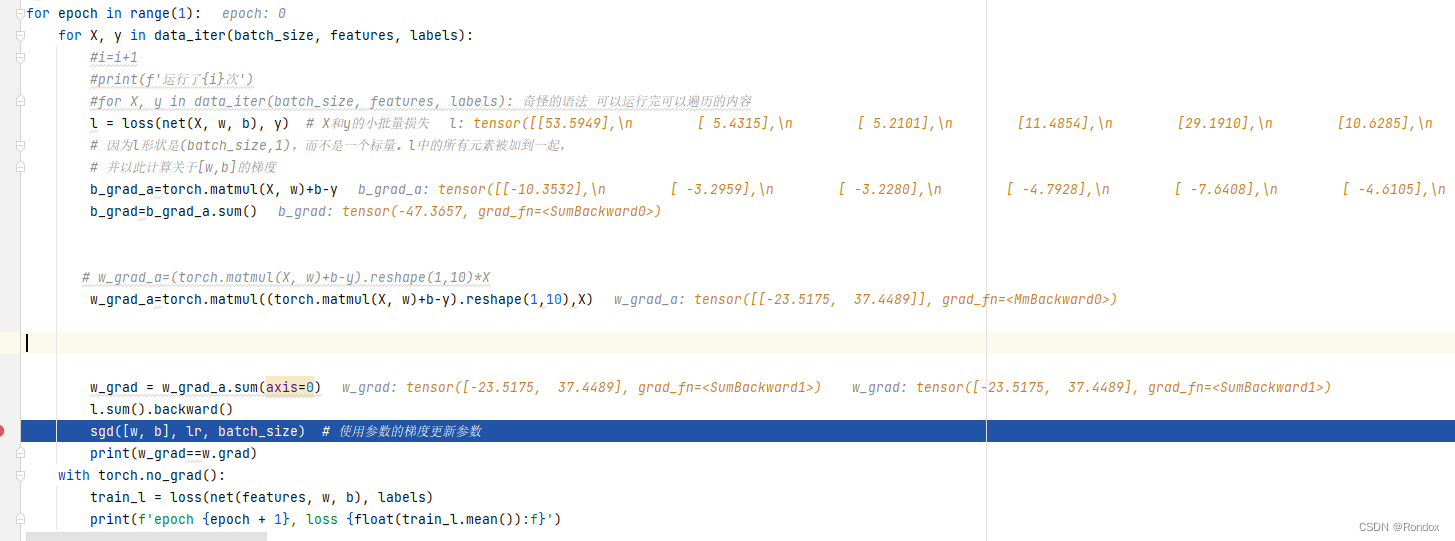
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！