贪心算法 —— 每时每刻都要做最好的( $ _ $ )
算法思想介绍
贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体 最优上加以考虑,他所做出的是在某种意义上的局部最优解。 贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行 的第一个基本要素。 当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。运用贪心策略在每一次转化时 都取得了最优解。问题的最优子结构性质是该问题可用贪心算法求解的关键特征。贪心算法的每一次操作都对 结果产生直接影响。贪心算法对每个子问题的解决方案都做出选择,不能回退。 贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保能获 得局部最优解。每一步只考虑一个数据,他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在 一起不再是可行解时,就不把该数据添加到部分解中,直到把所有数据枚举完,或者不能再添加算法停止。 实际上,贪心算法适用的情况很少。一般对一个问题分析是否适用于贪心算法,可以先选择该问题下的几个实 际数据进行分析,就可以做出判断。
总之:贪心算法,不考虑全局,每一步最优解,最终叠加组合,得到最优解,局部最优解就是当前最优解,就是解题的约束条件
过程
1. 建立数学模型来描述问题; 2. 把求解的问题分成若干个子问题; 3. 对每一子问题求解,得到子问题的局部最优解; 4. 把子问题的局部最优解合成原来解问题的一个解
简单来说就是:假设一个问题比较复杂,暂时找不到全局最优解,那么我们可以考虑把原问题拆成几个小问题(分而治 之思想),分别求每个小问题的最优解,再把这些“局部最优解”叠起来,就“当作”整个问题的最优解了
该算法存在的问题
不能保证求得的最后解是最佳的 不能用来求最大值或最小值的问题 只能求满足某些约束条件的可行解的范围
举例
通过下面的例子,了解贪心的思想吧~
选择排序
我们学的排序算法之一的选择排序,就用到了贪心的算法,我们可以通过每次遍历序列的方式寻找最小的数,将他与序列的第一个位置交换,然后再从剩下的位置中寻找最小的数,再次交换到前面去,最终就得到一个有序数组
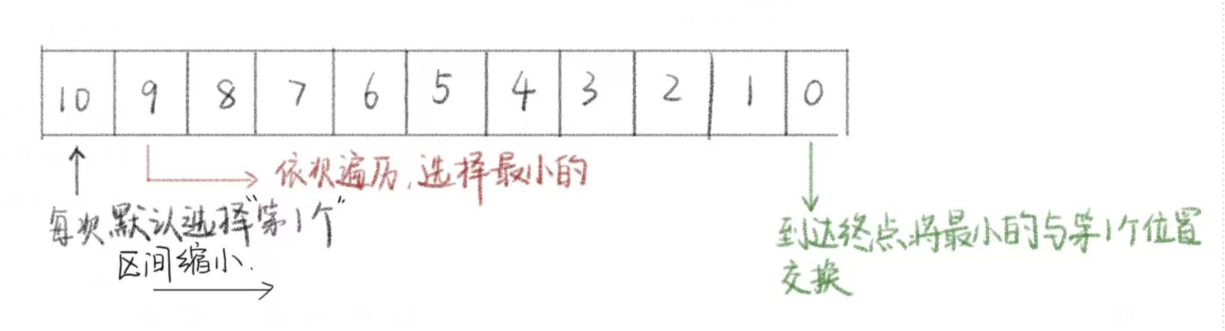
void selectSort(int* arr, int n)//arr数组(元素个数为n)排序
{for (int i = 0; i < n; ++i)//i限定了一段区间{int curIndex = i;//curIndex记录遍历所到之处目前最小元素的下标for (int j = i + 1; j < n; ++j){if (arr[curIndex] > arr[j])//遍历剩余元素,找到最小的元素下标curIndex = j;}swap(arr[curIndex], arr[i]);}
}平衡字符串
https://leetcode-cn.com/problems/split-a-string-in-balanced-strings/
平衡字符串 中,'L' 和 'R' 字符的数量是相同的。给你一个平衡字符串 s,请你将它分割成尽可能多的子字符串,并满足:
每个子字符串都是平衡字符串。返回可以通过分割得到的平衡字符串的 最大数量
示例:
输入:s = "RLRRLLRLRL"
输出:4
解释:s 可以分割为 "RL"、"RRLL"、"RL"、"RL" ,每个子字符串中都包含相同数量的 'L' 和 'R'
输入:s = "RLRRRLLRLL"
输出:2
解释:s 可以分割为 "RL"、"RRRLLRLL",每个子字符串中都包含相同数量的 'L' 和 'R' 。
注意,s 无法分割为 "RL"、"RR"、"RL"、"LR"、"LL" 因为第 2 个和第 5 个子字符串不是平衡字符串
输入:s = "LLLLRRRR"
输出:1
解释:s 只能保持原样 "LLLLRRRR"
思考方向:
题目要求尽可能多的分割,所以就不可以嵌套平衡,只要可以平衡就立刻分割,所以我们可以设定L为-1,R为+1,以这个角度看待数组,用balance表示前n项和,只要balance为0,就立刻更新分割数
class Solution {
public:int balancedStringSplit(string s) {int balance=0;int cnt=0;for(int i=0;i3. 买卖股票的最佳时机 II
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
解题思路:如果在连续上涨的第一天买下股票,在最后一天卖出,那么就可以得到最大收益,这也等价于第一天买入,最后一天卖出,中间的每天既买入又卖出,如果股票开始连续下跌,不可以买入也不卖出,因此遍历整个股票交易日价格列表,在上涨日都买卖,赚到所有利润,下降日什么也不要做,这样就永远不会亏钱
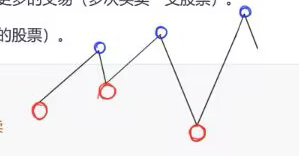
红点处买入,蓝点处卖出,红蓝之间既买又卖
class Solution {
public:int maxProfit(vector& prices) {int ret=0;for(int i=0;i0){ret+=curProfit;}}return ret;}
}; 4. 跳跃游戏
https://leetcode-cn.com/problems/jump-game/
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
这道题目比较好的思路就是站在每一个位置,更新所能到达的最远距离,如果发现在某一点所能到达的最远距离等于他下标本身那就不可能到达终点
class Solution {
public:bool canJump(vector& nums) {if(nums.size()==1)return true;int max=nums[0];for(int i=1;i=1 && max<=(nums[i]+i))max=nums[i]+i;if(max>=nums.size()-1)return true;if(max==i&&nums[i]==0)return false;}return false; }
}; 5 钱币找零
假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K 元,至少要用多少张纸币?
贪心策略: 用贪心算法的思想,很显然,每一步尽可能用面值大的纸币即可。在日常生活中我们自然而然也是这么做的。在程序中已经 事先将Value按照从小到大的顺序排好。
#include
#include
using namespace std;
int solve(int money,const vector>& moneyCount)
{int num = 0;//首先选择最大面值的纸币for (int i = moneyCount.size() - 1; i >= 0; i--){//需要的当前面值与面值数量取最小int c = min(money / moneyCount[i].first, moneyCount[i].second);money = money - c * moneyCount[i].first;num += c;}if (money > 0)num = -1;return num;
}
int main()
{//存放纸币与数量: first:纸币,second:数量vector> moneyCount = { { 1, 3 }, { 2, 1 }, { 5, 4 }, { 10, 3 }, { 20, 0},{50, 1}, { 100, 10 } };int money;cout << "请输入要支付的钱" << endl;cin >> money;int res = solve(money, moneyCount);if (res != -1)cout << res << endl;elsecout << "NO" << endl;return 0;
} 6 多机调度问题
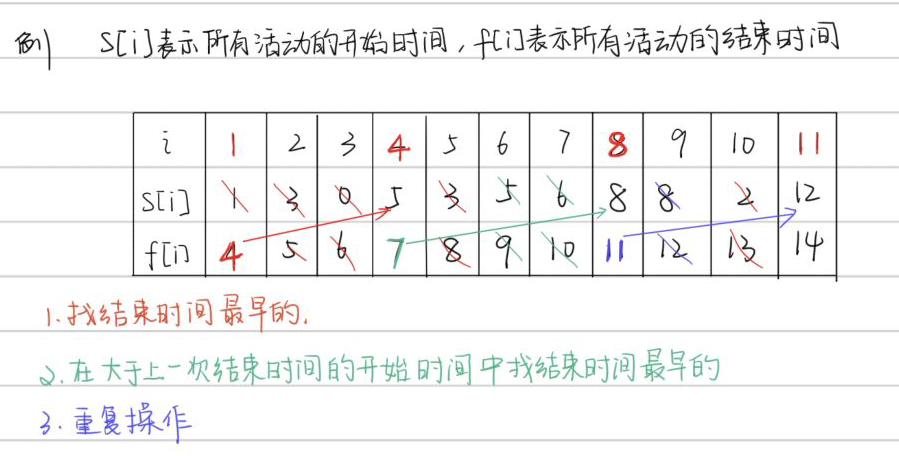
某工厂有n个独立的作业,由m台相同的机器进行加工处理。作业i所需的加工时间为ti,任何作业在被处理时不能中 断,也不能进行拆分处理。现厂长请你给他写一个程序:算出n个作业由m台机器加工处理的最短时间 输入 第一行T(1 处理策略: 当n<=m时,只要将作业分给每一个机器即可;当n>m时,首先将n个作业从大到小排序,然后依此顺序将作业分配给空闲的处 理机。也就是说从剩下的作业中,选择需要处理时间最长的,然后依次选择处理时间次长的,直到所有的作业全部处理完 毕,或者机器不能再处理其他作业为止。如果我们每次是将需要处理时间最短的作业分配给空闲的机器,那么可能就会出现 其它所有作业都处理完了只剩所需时间最长的作业在处理的情况,这样势必效率较低 。 代码实现 有n个需要在同一天使用同一个教室的活动a1, a2, …, an,教室同一时刻只能由一个活动使用。每个活动a[i]都有一个 开始时间s[i]和结束时间f[i]。一旦被选择后,活动a[i]就占据半开时间区间[s[i],f[i])。如果[s[i],f[i])和[s[j],f[j])互不重 叠,a[i]和a[j]两个活动就可以被安排在这一天。求使得尽量多的活动能不冲突的举行的最大数量。 问题分析: 1. 每次都选择开始时间最早的活动,不能得到最优解。 (因为极端情况下可能这个活动霸占一整天) 2. 每次都选择持续时间最短的活动,不能得到最优解。(因为可能这是持续时间最短的活动开始与结束时间与其他活动冲突 3. 每次选取结束时间最早的活动,可以得到最优解。按这种方法选择,可以为未安排活动留下尽可能多的时间。如下图所示的 活动集合S,其中各项活动按照结束时间单调递增排序 https://leetcode-cn.com/problems/non-overlapping-intervals/ 给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。 如果我们按照起点对区间进行排序,贪心算法就可以起到很好的效果。 按起始递增排序,找排序序列中第一个结束的,然后在剩下大于该结束位置的起始的序列中找到第一个结束的,重复这段过程 
bool cmp(const int &x, const int &y)
{
return x > y;
}
int findMax(const vector 7 活动选择
#include8 无重叠区间
class Solution {
public:
static bool cmp(const pair
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!