【learning】插头dp
问题描述
一种网格棋盘上的回路(路径也可以)数量统计之类的问题,也可以是求最优值之类的可以考虑dp求解的问题
具体解法
- 一些必须前置的东西
首先是一些概念的引入:
1、插头:既然是插头dp那肯定要先说说插头是啥,插头其实可以理解为每个格子的路经的走向,有以下几种情况:

2、轮廓线:就是下图中蓝色的那条东西,我们在转移的时候采用状态压缩的方式记录轮廓线的。。轮廓,然后一个一个格子来转移
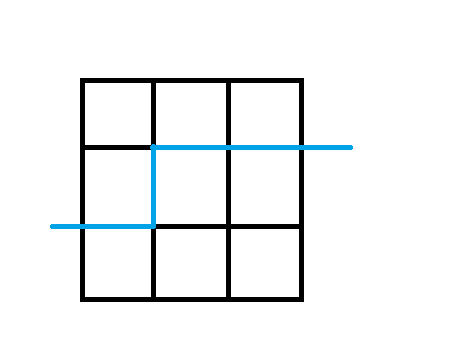
与一般的dp不同,插头dp是基于轮廓线的dp而不是基于格子的dp,这是很重要的一点
具体什么意思呢?就是说我们在记录和判断状态的时候,都是轮廓线对应的插头的状态
清楚了这些东西之后,我们来借助几道题更加具体地说说这个状态之类的东西到底是啥
Portal-->bzoj1814
(哇。。这题为啥是权限题。。)
简单说一下题面(其实就是论文题啦),给你一个\(m*n\)的棋盘,有的格子存在障碍不能走,求经过所有非障碍格子的哈密顿回路个数(\(1<=n,m<=12\))
我们考虑采用逐格递推的方式来求解,具体什么意思呢?其实就是cdq论文里面画的这个图,注意观察深蓝色的轮廓线的变化
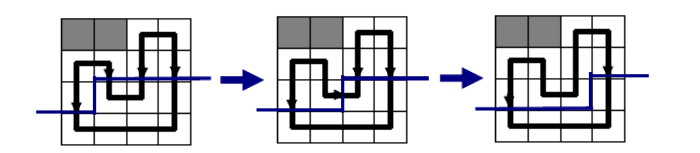
下面就是重头戏,状态的表示
由于这个是曼哈顿回路,所以有一个非常优秀的性质:连通路径不相交
思考一下对于一小段轮廓线我们需要记录什么信息:插头的方向和连通性,然后因为这里有这个不相交的优秀性质,所以我们可以巧妙利用一个括号匹配来解决
我们可以将状态分为三大类(图中蓝色的表示轮廓线,橙黄色是路径走向):
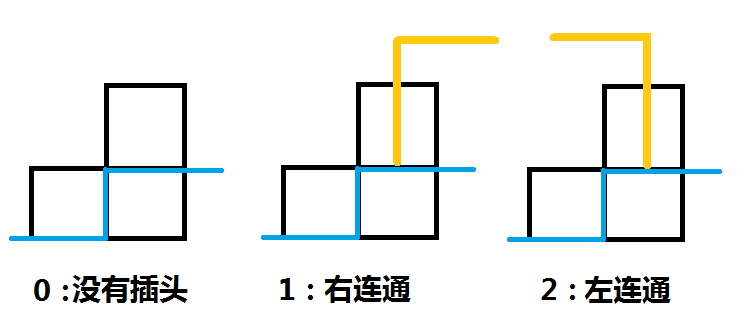
后面两类再说的具体一点就分别是“与右边的某处轮廓线的插头配对”和“与左边的某处轮廓线的插头配对”
我们转移的时候实际上是由\(L\)和\(U\)段的插头的状态推到\(D\)和\(R\)段的插头的状态:
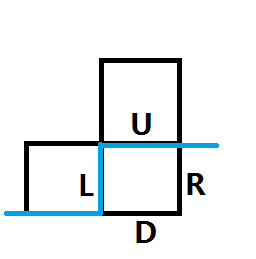
当考虑一个格子\((i,j)\)的转移的时候,我们需要关注的是这个格子左边界的轮廓线(提取状态出来之后是第\(j\)段轮廓线)对应的插头和上边界轮廓线(第\(j+1\)段轮廓线)对应的插头,那么接下来就是愉快的大力分类讨论时间:
1、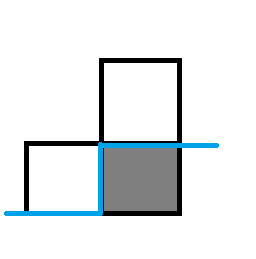
这个格子是障碍,那么如果说上面和左边都没有路径过来(没有插头的话,说明路径绕过了这个障碍,状态合法,如果有则不合法,不转移
2、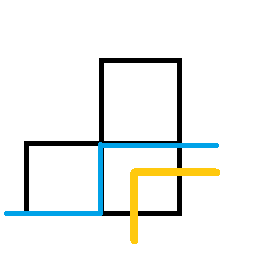
这个格子不是障碍并且上、左都没有路径过来,那么我们可以考虑新加一个“转角”(如上图),那也就是\(j\)段插头状态变成\(1\),\(j+1\)段插头状态变成\(2\)
3、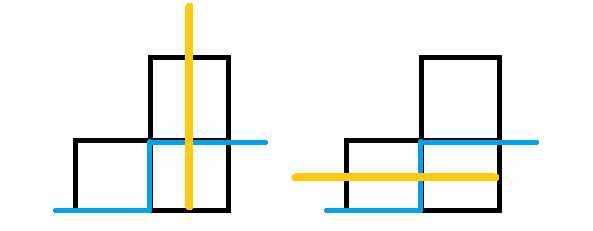
这个格子不是障碍并且左边或上面有一个没有路径过来,那就直接延伸原来的路径就好了
4、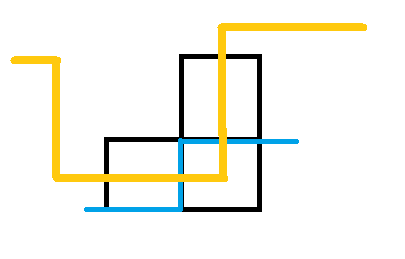
这个格子不是障碍并且左边的是一个通向左边的插头,上面的是一个通向右边的插头,那么显然中间必须要连起来了,所以新的状态中\(j\)段和\(j+1\)段都是没有插头的
5、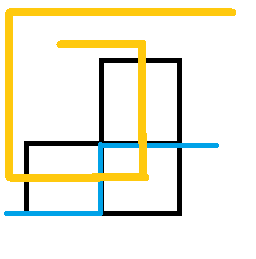
这个格子不是障碍并且左插头通向右边,上插头通向左边,那么这个时候就应该统计答案了(因为已经围成了一个回路),判断一下轮廓线上是否只有这两个地方是有插头的,如果是的话说明只有一条回路,可以作为一个答案
6、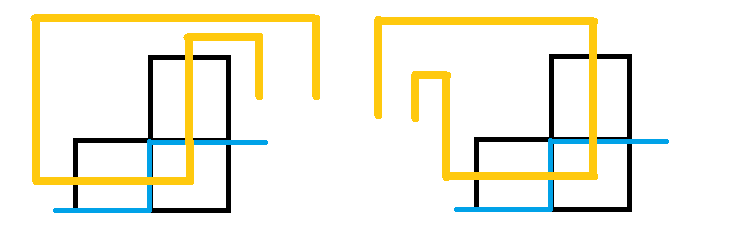
这个格子不是障碍并且左插头和上插头同向,那么这个时候也是应该在\((i,j)\)这个格子连起来,然后这样一来,左插头或者上插头原先对应的那个匹配的插头状态需要调整(因为一旦连通起来了就不可能有两对\(1,2\)状态的插头,而是应该只有一对),以第一幅图为例,当两个插头都是\(1\)插头的时候,上插头原来对应的\(2\)插头应该要变为\(1\)插头,因为与之配对的插头到右边去了;然后如果在第二幅图里面的话,就应该是左插头对应的\(1\)插头变为\(2\)插头
就此我们十分愉快地讨论完了,然后这题就这样做完了
这里有一个小trick就是,虽然说插头状态只有三个,但是其实为了快,我们完全可以用一个四进制数来存(这样就可以直接位运算了嘛),大力哈希一下就好了
然后对于情况6中的寻找与之配对的插头这个,我们可以直接用括号匹配的方式来寻找
其实想明白了还是挺好写的就是调试的时候会有点恶心qwq
代码大概长这个样子(不过说实话感觉插头dp还是自己写一遍比较清楚)
#include
#include
#include
#include
#define ll long long
#define behind 1
#define front -1
using namespace std;
const int N=12+3,HS=2333,TOT=1e6+10;
int n,m,edi,edj;
struct Hash{/*{{{*/int st[TOT],hd[HS],nxt[TOT];ll sum[TOT];int tot;void add(int x,int id,ll data){st[++tot]=id; nxt[tot]=hd[x]; hd[x]=tot; sum[tot]=data;}void insert(int id,ll data){int x=id%HS;for (int i=hd[x];i;i=nxt[i])if (st[i]==id){sum[i]+=data;return;}add(x,id,data);}void clear(){for (int i=0;i>=((x-1)<<1); return st-((st>>2)<<2);}//4 jinzhi
void add_st(int j,int st,ll val){h[now].insert(j==m?((st-query(st,m+1)*pw[m])<<2):st,val);}
void change(int &st,int x,int val){st+=(val-query(st,x))*pw[x-1];}
int find(int st,int x,int mark);int main(){
#ifndef ONLINE_JUDGEfreopen("a.in","r",stdin);
#endifchar ch;scanf("%d%d\n",&n,&m);for (int i=1;i<=n;++i){for (int j=1;j<=m;++j){scanf("%c",&ch);mp[i][j]=ch=='.';if (ch=='.') edi=i,edj=j;}scanf("\n");}init();solve();printf("%lld\n",ans);
}void init(){pw[0]=1;for (int i=1;i<=12;++i) pw[i]=pw[i-1]<<2;ans=0;
}void solve(){now=1,pre=0;h[pre].insert(0,1);for (int i=1;i<=n;++i){for (int j=1;j<=m;++j){h[now].clear();if (i==4&&j==1)int debug=1;dp(i,j);swap(now,pre);}}
}void dp(int i,int j){h[pre].TakeOut(rec_st,rec_sum,len);int st,plugl,plugu,nw,pos;ll val;while (len){st=rec_st[len]; val=rec_sum[len]; --len;plugl=query(st,j);plugu=query(st,j+1);if (!mp[i][j]){//not okif (plugl==0&&plugu==0)add_st(j,st,val);continue;}if (plugl==0&&plugu==0){add_st(j,st,val);if (i
Portal-->bzoj3125
有了上面那题的铺垫,这题做起来就。。其实差不多嘛
不同的是,有些块的方向是固定的,那么这个只要在上面分的几大类中再单独判断一下就好了
下面附上dp部分的代码
void dp(int i,int j){h[pre].TakeOut(rec_st,rec_sum,len);int st,plugl,plugu,nw,pos;ll val;while (len){st=rec_st[len]; val=rec_sum[len]; --len;plugl=query(st,j);plugu=query(st,j+1);if (mp[i][j]=='#'){//not okif (plugl==0&&plugu==0)add_st(j,st,val);continue;}if (plugl==0&&plugu==0&&mp[i][j]=='.'){if (i
Portal -->bzoj1187
这题的话,不同的只是多了一个满意度,那么直接把计算方案数改成满意度取max就好了
长得都差不多代码就。。不贴了吧
Portal -->bzoj2310
最后这题,就是重头戏了(然而还是权限题。。)
说一下题面:给你一个\(m*n\)的矩阵,每个格子有一个权值\(v(i,j)\),权值可能是负数,要求找一条路径,使得每个点最多经过一次,并且经过的点权值和最大
好的,我们发现这题不再是求回路了,那么怎么办?
其实我们只需要多一个插头状态就可以解决这个问题了,我们多加一个插头状态\(4\),表示这是一个独立插头,具体什么意思呢?就是因为现在我们求的不是回路了,所以并不是所有的插头都两两匹配,有的插头是作为整条路径的一端,那么我们将这种插头称为独立插头
接下来依旧是原来的处理方式和转移方式,我们继续开始愉快分类讨论,有了前面的示例,这里就不再画图了,为了让描述变得更加简洁,下面我们用\(plugu\)表示上边界插头的状态,\(plugl\)表示左边界插头的状态,转移后对应\(plugr\)表示右边界插头的状态,\(plugd\)表示左边界插头的状态
1、\(plugl=0,plugu==0\):
当前的格子可能成为路径的一端,也就是转移后\(plugr=4\)或者\(plugd=4\),另一个就为\(0\)
2、\(plugl=0\)或\(plugr=0\):
如果说没有超出边界的话,显然可以继续延伸(也就是例题一种的情况6)
此外如果说非零的那个插头是独立插头,那么我们判断是否只有一条路径然后就可以更新答案了
如果说非零的那个插头不是独立插头而是\(1\)或者\(2\)插头的话,说明它可以成为路的一端作为一个独立插头,对应的这个插头原来对应的位置也要变成独立插头
3、\(plugl=3,plugu=3\):
这种情况下也是判断一下是否只有一条路径,然后就可以更新答案了
4、\(plugl=1或2,plugu=3\):
连起来之后,\(plugl\)原来对应的插头要变成独立插头作为路径的另一端存在
5、\(plugl=3,plugu=1或2\):
跟情况4类似
6、其他的\(plugl<=2,plugu<=2\)的情况,都与例题一中的讨论情况一致
同样也是。。想明白了之后很好写但是!调试起来很恶心qwq
同样是建议自己写qwq
不过同样还是附上参考代码qwq
#include
#include
#include
#define ll long long
#define front -1
#define behind 1
using namespace std;
const int N=10,HS=2333,TOT=1e6+10;
const ll inf=1LL<<60;
struct Hash{/*{{{*/int nxt[TOT],id[TOT],st[TOT],hd[TOT];ll val[TOT];int tot;void add(int x,int id,ll data){st[++tot]=id; nxt[tot]=hd[x]; hd[x]=tot; val[tot]=data;}void insert(int id,ll data){if (id==1)int debug=1;int x=id%HS;for (int i=hd[x];i;i=nxt[i])if (st[i]==id){val[i]=max(val[i],data);return;}add(x,id,data);}void clear(){for (int i=0;i>=((x-1)<<1);return st-((st>>2)<<2);}
void change(int &st,int x,int val){st+=(val-query(st,x))*pw[x-1];}
void add_st(int st,int j,ll val){h[now].insert(j==m?(st-query(st,m+1)*pw[m])<<2:st,val);}
int find(int st,int x,int step);
void solve();
void dp(int i,int j);
int calc(int st);int main(){
#ifndef ONLINE_JUDGEfreopen("a.in","r",stdin);
#endifscanf("%d%d",&n,&m);for (int i=1;i<=n;++i)for (int j=1;j<=m;++j)scanf("%lld",&v[i][j]);prework();solve();printf("%lld\n",ans);
}void prework(){pw[0]=1;for (int i=1;i>=2)ret+=(st-((st>>2)<<2))==3;return ret;
}void dp(int i,int j){int st,plugl,plugu,pos,which,dir,nw;ll val;h[pre].TakeOut(rec_st,rec_val,len);while (len){st=rec_st[len]; val=rec_val[len]; --len;plugl=query(st,j);plugu=query(st,j+1);nw=st;if (plugl==0&&plugu==0){//(0,0)add_st(st,j,val);if (i
最后附上参考资料:Portal -->cdq论文
转载于:https://www.cnblogs.com/yoyoball/p/9348216.html
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!