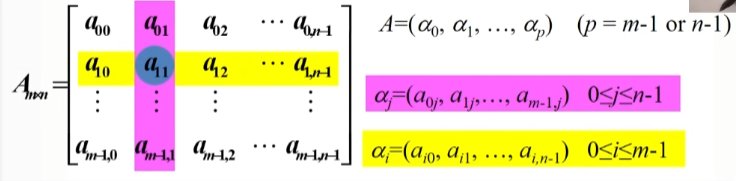文章目录

• 一、数组的定义及特点
• 二、数组的抽象数据类型定义
• 三、数组的顺序存储
• • 1. 一维数组
  • 2. 二维数组
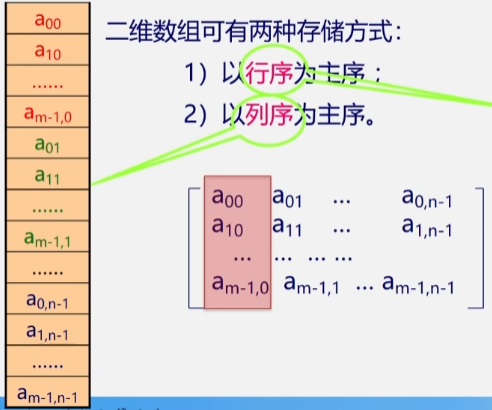
  • • 2.1 以行序为主序
    • 2.2 以列序为主序
• 四、特殊矩阵的压缩存储
• • 1. 对称矩阵
  • 2. 三角矩阵
  • 3. 对角矩阵
  • 4. 稀疏矩阵
  • • 4.1 十字链表

一、数组的定义及特点

数组

• 按照一定格式排列起来的，具有相同类型的数据元素的集合。

一维数组

• 若线性表中的数据元素为非结构的简单元素，则称为一维数组。
• 逻辑结构：线性结构。定长的线性表
• 声明格式：数据类型 变量名 [数组长度]。
  • 如：int num [5] = {0，1，2，3，4};

二维数组

• 若一维数组中的数据元素又是一维数组结构，则称为二维数组。
• 逻辑结构：
  • 非线性结构：每一个数据元素既在一个行表中，又在一个列表中。
  • 线性结构（定长的线性表）：该线性表的每个数据元素也是一个固定长度的线性表。
• 声明格式：数据类型 变量名[行数][列数]；
  • 如 int A [3][4]，这样就定义了一个名为A的数组内每个元素都是 int 类型的三行四列的二维数组出来了。

• 除了4个角落的元素之外，每个元素都有不止一个前趋和后继，比如说这里的 a11，在它所在的这一行有前趋 a10 和后继 a12，在它所在的这一列里，又有 a01 这个前趋和 。。。这个后继。

三维数组

• 若二维数组中的元素又是一个一维数组，则称之为三维数组。

n 维数组

• 若 n-1 维数组中的元素又是一个一维数组结构，则称作 n 维数组。

结论

• 线性表结构时数组结构的一个特立，而数组结构又是线性表结构的扩展。

数组特点

• 结构固定 —— 定义后，维数和维界不再改变。

数组基本操作

• 除了结构的初始化和销毁之外，只有取元素和修改元素值的操作。
• 不会说有什么插入或者删除数组中的某个元素的操作。

二、数组的抽象数据类型定义

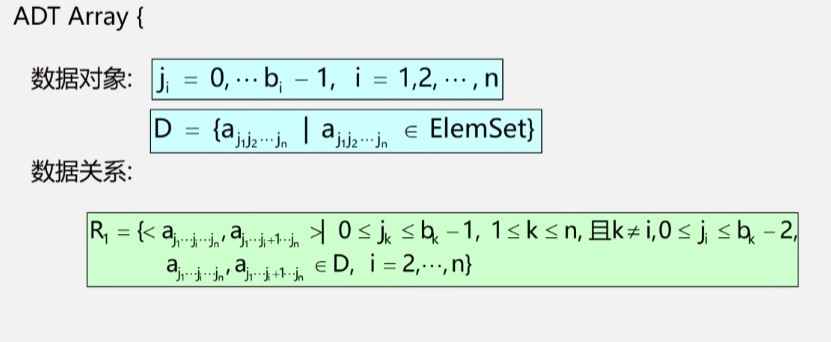
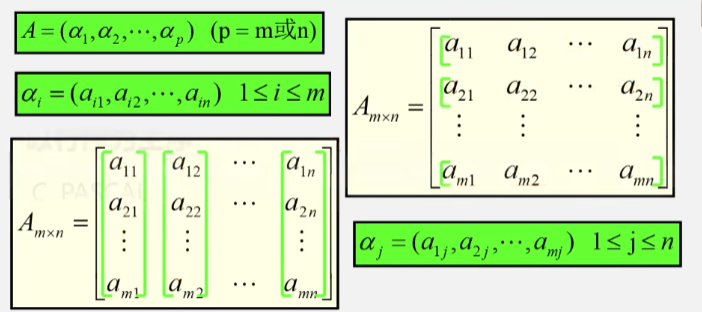
n 维数组的抽象数据类型

• n 为数组的维数（一维数组、二维数组…）。
• bi 为数组第 i 维的长度。
• ji 为数组元素第 i 维的下标。

举个例子：

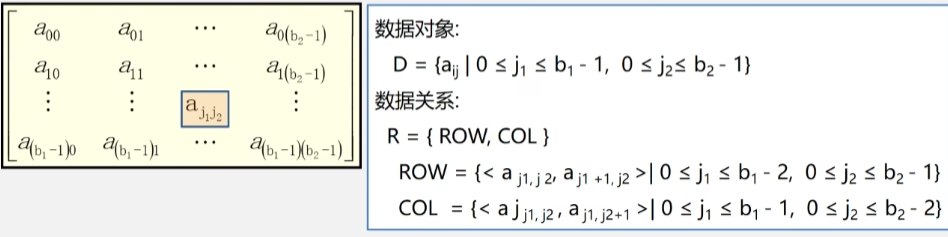
• 二维数组的抽象数据类型的数据对象和数据关系的定义。

  • n = 2（维数为2，二维数组）。
  • b₁：第 1 维长度（行数）；b₂：第 2 维长度（列数）。
  • aj₁j₂：第 1 维下标为 j₁，第 2 维下标为 j₂。

基本操作

1. 构造数组 A：==InitArray(&A,n,bound1,…boundn)。
2. 销毁数组 A：DestroyArray(&A)。
3. 取数组元素值：Value(A,&e,index1,…,indexn)。
4. 给数组元素赋值：Assign(A,&e,index1…,indexn)。

三、数组的顺序存储

数组特点

• 结构固定，固定以后，维数和维界不再改变，所以比较适合采用顺序存储结构。

数组基本操作

• 除了结构的初始化和销毁之外，只有取元素合修改元素值的操作。
• 不会说有什么插入或者删除数组中的某个元素的操作。

注意

• 数组可以是多维的，但存储数据元素的内存单元地址是一维的；
• 因此，在存储数据结构之前，需要解决将多维关系映射到一维关系的问题。

1. 一维数组

• 例，有数组定义：int a [5];
  • 每个元素占用4个字节，假设 a[0] 存储在2000单元的位置，a[3] 应该在 2012 的位置上，2000 + （3 - 0）* 4。

• 下标为 3 的元素前面有 3 个元素，如果是下标为 i 的元素，则前面有 i 个元素，第 i 个元素的位置应该是首元素的地址+i * 每个元素的大小——>LOC(i) = a + i * L 。

2. 二维数组

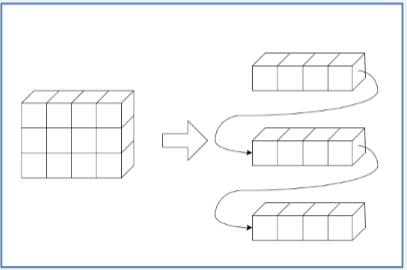
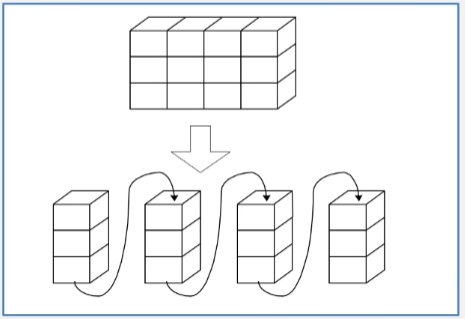
• 假设一个 m 行 n 列的二维数组，每一行都有 n 个元素，每列都有 m 个元素。

• 这样一个二维数组可以看成是由若干行组成的，每一行都是一个一维数组。

• 也可以看成是由若干列组成的，每一列都是一个一维数组。

两种顺序存储方式

• 以行为主序（低下标优先）BASIC、COBOL 和 PASCAL。
• 以列为主序（高下标优先）FORTRAN。

2.1 以行序为主序

• 存储单元是一维结构，而数组是个多维结构，则用一组连续存储单元存放数组的数据元素就有个次序约定问题。
• 按照行来存储，存储完第一行之后再存储第二行，以此类推。
• 要查找某个元素的话就要找到对应的行列位置，如：第一行一列的元素就在 [0][0] 的位置，第二行第二列的元素就在下标为 [1][1] 的位置。

• 每一行都从第一个元素开始存储直到存储到下标为 n - 1 的位置然后就换下一行存储。
• 第一行的首元素下表为 [0][0]，最后一行的首元素下标则为 [m - 1][0]。

以行序为主序的存储位置计算

• 设数组开始存储位置为LOC(0,0)，存储每个元素需要 L 个存储单元（字节）。
• 数组元素 a[i][j] 的存储位置是：LOC(i,j) = LOC(0,0) + (n * i + j) * L。
  • （数组总列数 * i 行 + j 列）* 元素大小。

2.2 以列序为主序

• 按照列来存储，存储好一列之后再存储下一列。

• 先从第一列开始存，第一列的首元素存到最后一个元素的下标应该是 a[0][0]（首行首列），a[1][0]（二行一列）a[2][0]）（三行一列）以此类推直到 a[m - 1][0]（m行1列）。

四、特殊矩阵的压缩存储

矩阵

• 一个由 m * n 个元素排成的 m 行 n 列的表。
• 有时为了节省存储空间，可以对这类矩阵进行压缩存储。

矩阵的常规存储

• 将矩阵描述为一个二维数组。

矩阵的常规存储的特点

• 可以对其元素进行随机存取。
• 矩阵运算非常简单，存储的密度为1。
  • 不需要额外的空间存放地址，分配100个字节的空间就能存储100字节的数据。

不适合常规存储的矩阵

• 值相同的元素很多且呈某种归路分布；零元较多。

矩阵的压缩存储

• 为多哥相同的非零元素只分配一个存储空间；对零元素不分配空间。

1. 什么是压缩存储

• 若多个数据元素的值都相同，则只分配一个元素值的存储空间，且零元素不占存储空间。

2. 什么样的矩阵能够压缩？

• 一些分布有规律的矩阵；
• 对称矩阵、对角矩阵、三角矩阵、稀疏矩阵等。

3. 什么是稀疏矩阵

• 矩阵中非零元素的个数较少（一般小于 5%）
• 有 95% 以上的元素是零，不需要给这些元素分配空间，一下节省 95% 的空间。

1. 对称矩阵

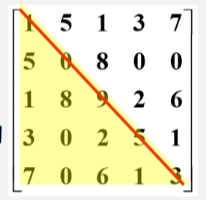
• 沿着对角线相等的矩阵就称为对称矩阵。

特点

• 在 n x n 的矩阵 a 中，满足如下性质：aij = aji (1 <= i,j <= n)。
• 比如说上图中 a[4][1] = a[1][4]

对称矩阵的存储方式

• 因为元素是按照对角线来存储的，另一半是一样的元素，不需要全部存；
• 只存储下（或者上）三角（包括主对角线）的数据元素。
  • 共占用 n(n + 1) / 2 ，项数 *（首项 + 末项）/ 2个元素空间。

对称矩阵的存储结构

• 对称矩阵上下三角中的元素数均为：n(n + 1) / 2。
• 可以以行序为主序将元素存放在一个一维数组 sa[n(n + 1) / 2]中。

• 下标用 k 来表示，第一行放1个元素进a[0]中，第二行放两个进a[1]，a[2]中，以此类推。

2. 三角矩阵

特点

• 对角线以下（或以上）的数据元素（不包括对角线）全部为常数 C (所有值一样)。

三角矩阵的存储方式

• 重复元素 C 共享一个元素存储空间，总共占用 n(n + 1) / 2 + 1个元素空间：sa[1…n(n+1) / 2+1]。
• 上三角矩阵 sa[k] 和矩阵元 aij 之间的对应关系为：

• 下三角矩阵 sa[k] 和矩阵元 aij 之间的对应关系为：

3. 对角矩阵

特点

• 在 n x n 的方阵中，所有非零元素都集中在以主对角线为中心的带状区域中（只在对角线和对角线旁边有值），区域外的值全是 0 ，则称为对角矩阵。
• 常见的有三对角矩阵、五对角矩阵、七对角矩阵。
  • 如下图：只有在三条对角线的范围内有值。再加两条有值的对角线就是五对角矩阵了，依次类推。

对角矩阵的存储方式

• 为 0 的元素直接扔掉不存。
• 用二维数组的方式去存。

• 按对角线来存储，第一条对角线是 3385，则将3385 存在二维数组的第一行，第二条对角线是 20612 则存在第二行，以此类推。
• 以主对角线为0，看主对角线有几个元素，决定二维数组的每行要分配多少个元素的空间。
• 其余对角线进行上下对称。这样一个原本需要36个存储空间的矩阵现在就只需要30个了。

4. 稀疏矩阵

什么是稀疏矩阵?

• 矩阵中非零元素的个数较少（一般小于 5%）
• 有 95% 以上的元素是零，不需要给这些元素分配空间，一下节省 95% 的空间。
  • 在这样有 42 个元素的矩阵中非零元素只有 8 个，如果将零也存储起来就非常浪费空间了，存储密度只有 19.05%左右。

稀疏矩阵的存储方式

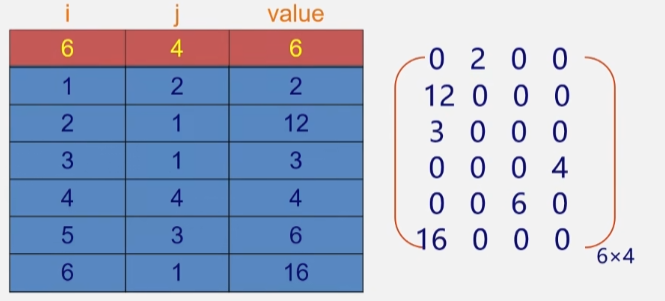
• 三元组：每个非零元素由它所在的行列和它本身的值来确定（i,j,aij）。
  • 比如下图的第一个元素12，它的存储就是 1 行 2 列值 12 确定。

压缩存储原则

• 存各非零元素的值，行列位置和矩阵的行列数。
  • 三元组的不同表示方法可以决定稀疏矩阵不同的压缩存储方法。
• 第 0 行表示存储的这个矩阵有几行几列几个非零元素，其余每行就是按顺序存储非零元素的行列值了。

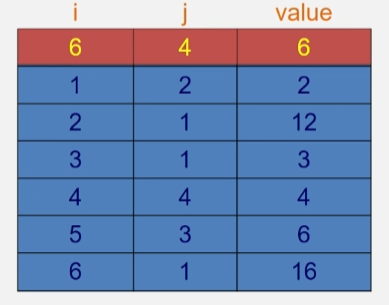
还原稀疏矩阵

• 试还原出下列三元组所表示的系数矩阵。

• 第一行的 646 表示原来的稀疏矩阵有 6 行 4 列 6 个非零元素。
• 非零值按照 i 和 j 所代表的行列位置以及将 value 值存放到具体位置。
  • 如：第二行的 122 表示值为 2 的元素出现在1行 2 列的位置，其余同理。
• 其余所有位置全部补 0 。

• 三元组顺序表又称有序的双下标法。

三元组顺序表的优缺点

• 优点：非零元素在表中按行执行有序存储，因此便于进行依行顺序处理的矩阵运算。
• 缺点：缺点同样是因为按行处理的，导致不能随机存取。
  • 若按行号存取某一行中的非零元，则需要从头开始进行查找。
  • 这个时候就需要用到稀疏矩阵的链式存储结构：十字链表了。

4.1 十字链表

• 优点：能够灵活地插入因运算而产生的新的非零元素，删除因运算而产生的新的零元素，实现矩阵的各种运算。

• 在十字链表中，矩阵的每一个非零元素用一个结点表示，该结点除了（row,col,value）以外，还要有两个域。

  • right ：用于链接同一行中的下一个非零元素。
  • down：用于链接同一列中的下一个非零元素。

• 十字链表中结点的结构示意图：

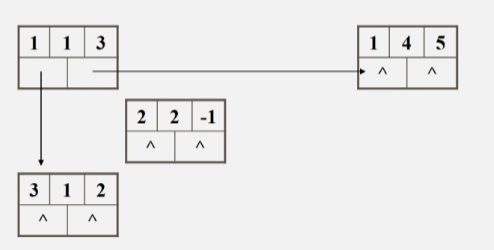
【例1】

• 假设有这样一个矩阵 m

• 先要存储第一个非零元素 3 ，需要知道与它同一行的下一个元素 5 的位置，以及同列的下一个元素 2 的位置。

• 此时还需要1个结点来存储 -1，同样，因为与 -1 同行同列的已经没有非零元素了，所以 right 及 dawn 域都置空。

• 此时还需要两个分别指向每行每列的头指针数组，在这样一个十字链表中，有三行，所以就需要弄一个存储三个头指针的数组，列同理。

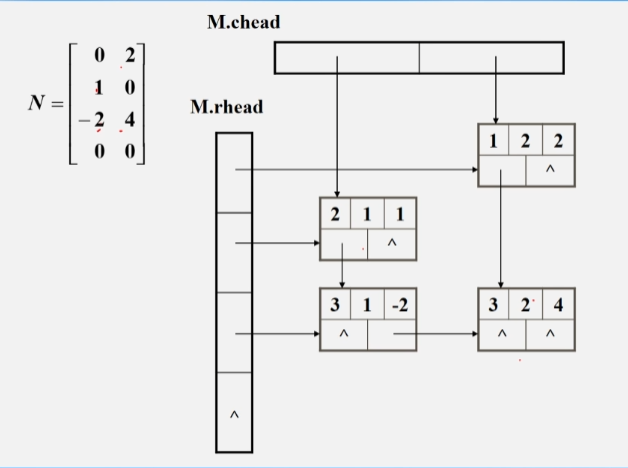
【例2】

• 稀疏矩阵中，有几行就要有几个行头指针，有几列就要有各个列头指针。
• 这些指针都指向 行/列 中的第一个元素。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！