高数_第6章无穷级数_幂级数的性质及其应用__和函数
幂级数有以下重要的性质
性质1 和函数连续性
设幂级数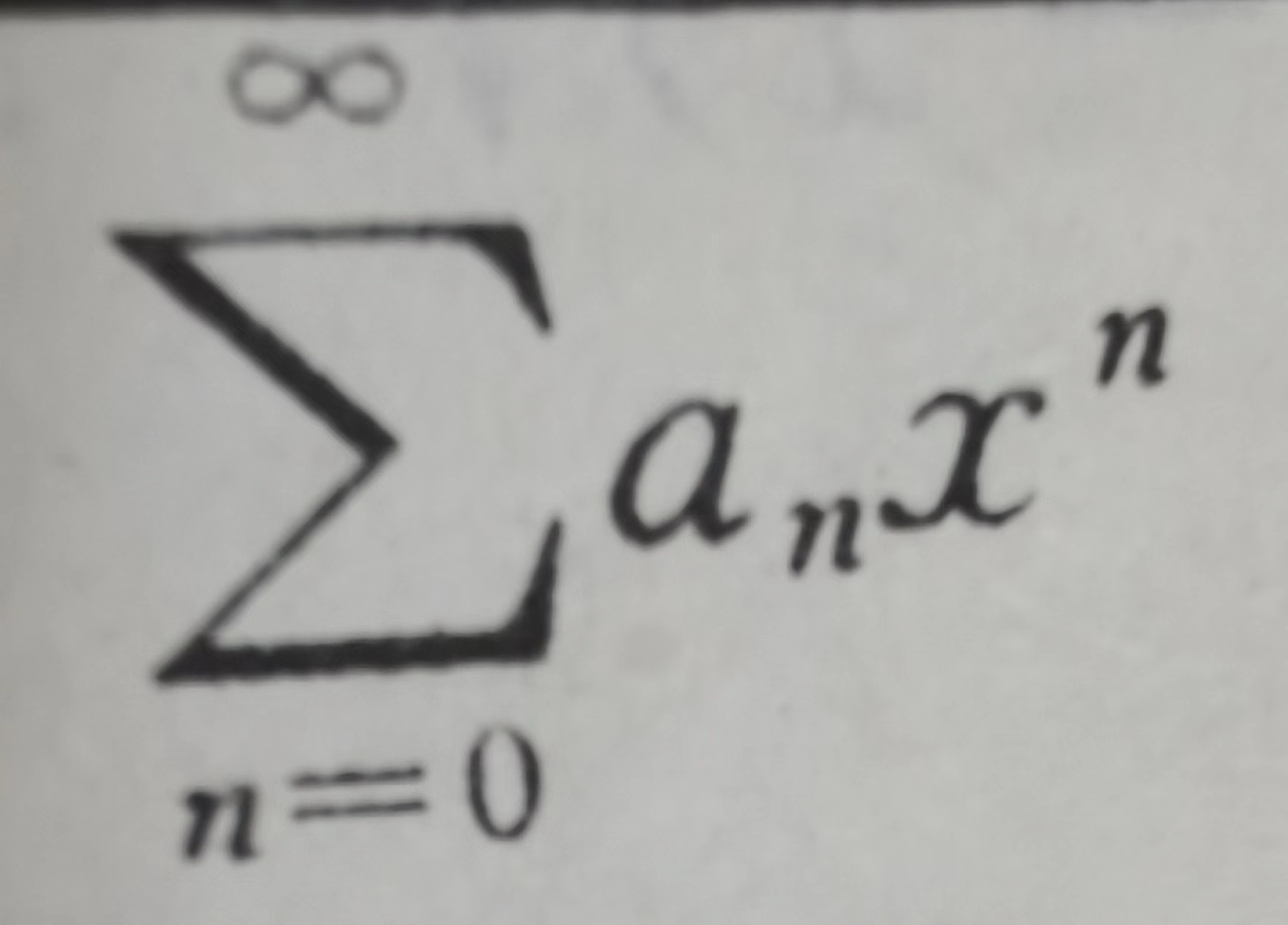 
的收敛半径为R (0< R ≤ +∞), 则其和函数s(x) 在(-R, R)内连续， 如果它在x = R或(-R)处收敛， 则和函数s(x)在(-R, R] (或 [-R, R))上连续。
性质2 逐项积分
设幂级数 的收敛半径为R (0< R ≤ +∞), 则其和函数s(x) 在(-R, R)内是可积的，对一切的x ∈（-R, R）有逐项积分公式
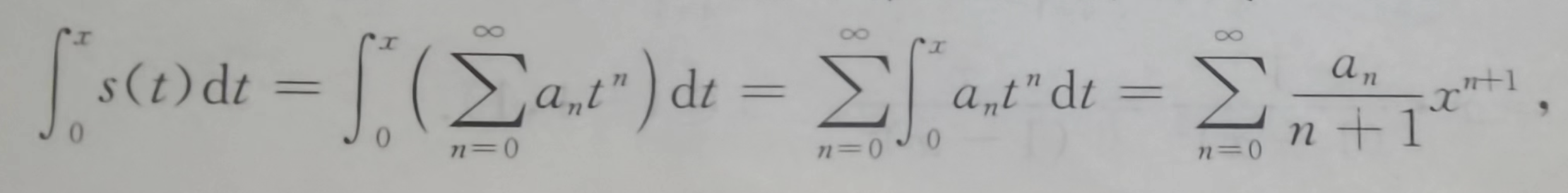
性质3 逐项求导
设幂级数 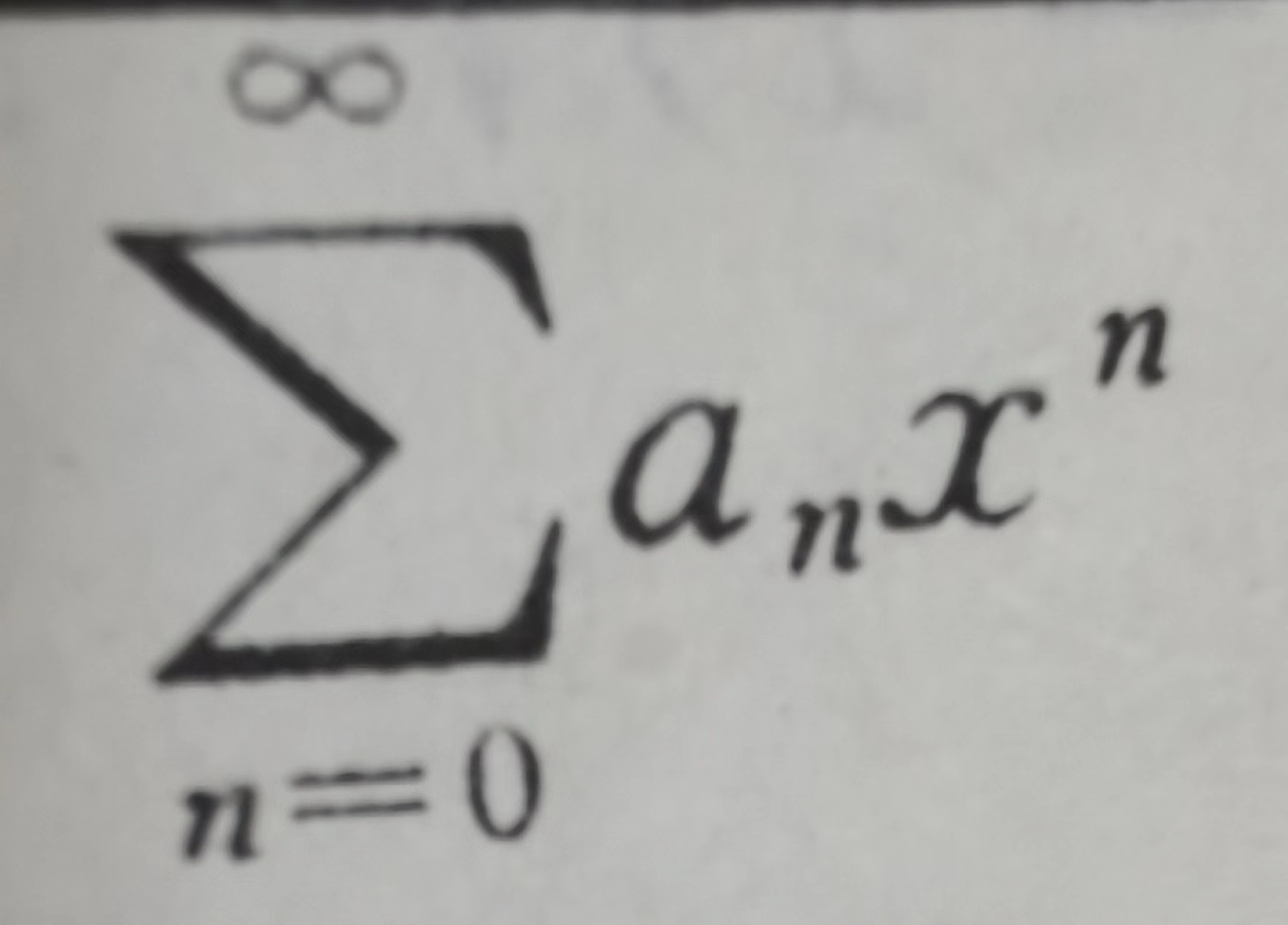的收敛半径为R (0< R ≤ +∞), 则其和函数s(x) 在 (-R, R)内是
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！