笔试编程题常用框架/方法
考试注意事项
先审完题意，再动手
在本地编辑器（有提示）
简单题5+15min
通过率0%，有额外log
考核方式
ACM模式
自己构造输入格式，控制返回格式，OJ不会给任何代码，不同的语言有不同的输入输出规范。
通过率0%时，检查是否有额外log
JavaScript(V8)
ACMcoder OJ
单行readline()(1024)/gest(n)(回车)
str-> num arr：line.split(' ').map(Number)
输出printsth/log/print(sth,...)(回车)
key：
read_line()//将读取至多1024个字符，一定注意看题目字符上限
gets(n)//将读取至多n个字符，当还未达到n个时如果遇到回车或结束符，回车符可能会包含在返回值中。printsth(sth, ...)//多个参数时，空格分隔；最后不加回车。
console.log(sth, ...)、print(sth, ...)//多个参数时，空格分隔；最后加回车line.split(' ').map(e=>Number(e));//str->arr
arr.push([]);//arr[]->arr[][]//单行输入
while(line=readline()){//字符数组var lines = line.split(' ');//.map(Number)可以直接将字符数组变为数字数组var lines = line.split(' ').map(Number); var a = parseInt(lines[0]);//效果等同下面var b = +lines[1]; //+能将str转换为numprint(a+b);
}//矩阵的输入
while (line = readline()) {let nums = line.split(' ');//读取第一行var row = +nums[0];//第一行的第一个数为行数var col = +nums[1];//第一行的第二个数为列数var map = [];//用于存放矩阵for (let i = 0; i < row; i++) {map.push([]);let mapline = readline().split(' ');for (let j = 0; j < col; j++) {map[i][j] = +mapline[j];}}
}
JavaScript(Node)
华为只可以采用Javascript(Node)
校招笔试真题_C++工程师、golang工程师_牛客网
while(line = await readline()){ }
rl.on('line', function(line){...}).on('close', function(){...})
模板1
var readline = require('readline')
// 创建读取行接口对象
const rl = readline.createInterface({input: process.stdin,output: process.stdout
})
单行
//监听换行，接受数据
rl.on('line', function(line) {//line为输入的单行字符串，split函数--通过空格将该行数据转换为数组。var arr= line.split(' ')//数组arr的每一项都是字符串格式，如果我们需要整型，则需要parseInt将其转换为数字console.log(parseInt(arr[0]) + parseInt(arr[1]));
})多行
const inputArr = [];//存放输入的数据
rl.on('line', function(line){//line是输入的每一行，为字符串格式inputArr.push(line.split(' '));//将输入流保存到inputArr中（注意为字符串数组）
}).on('close', function(){console.log(fun(inputArr))//调用函数并输出
})//解决函数
function fun() {xxxxxxxxreturn xx
}
模板2
const rl = require("readline").createInterface({ input: process.stdin });
//比模版1多的：
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;void async function () {// Write your code herewhile(line = await readline()){let tokens = line.split(' ');let a = parseInt(tokens[0]);let b = parseInt(tokens[1]);console.log(a + b);}
}()数组
前缀和-区间求和
差分数组-区间增减
想对区间 nums[i..j] 的元素全部加 3，那么只需要让 diff[i] += 3，然后再让 diff[j+1] -= 3
滑动窗口-子串：r++可行解->l--最短解
int left = 0, right = 0;while (right < s.size()) {// 增大窗口window.add(s[right]);right++;while (window needs shrink) {// 缩小窗口window.remove(s[left]);left++;}
}1、我们在字符串S中使用双指针中的左右指针技巧，初始化left = right = 0，把索引左闭右开区间[left, right)称为一个「窗口」。
2、我们先不断地增加right指针扩大窗口[left, right)，直到窗口中的字符串符合要求（包含了T中的所有字符）。
3、此时，我们停止增加right，转而不断增加left指针缩小窗口[left, right)，直到窗口中的字符串不再符合要求（不包含T中的所有字符了）。同时，每次增加left，我们都要更新一轮结果。
4、重复第 2 和第 3 步，直到right到达字符串S的尽头。
这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解
链表
虚拟头结点
let ret = new ListNode(0, head), temp = ret;双指针（快慢指针）：数组有序
单链表的中点/链表环：slow+1，fast+2
有序数组的平方
删除/覆盖数组元素
if(nums[i] != val){nums[k++] = nums[i]}最小长度的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
let ans = Infinitywhile(end < len){sum += nums[end];while (sum >= target) {ans = Math.min(ans, end - start + 1);sum -= nums[start];start++;}end++;}三数之和a+b+c=target
arr.sort()let l = i + 1, r = len - 1, iNum = nums[i]// 数组排过序，如果第一个数大于0直接返回resif (iNum > 0) return res// 去重if (iNum == nums[i - 1]) continueres.push([iNum, lNum, rNum])// 去重while(l < r && nums[l] == nums[l + 1]){l++}while(l < r && nums[r] == nums[r - 1]) {r--}l++r--四数之和a+b+c+d=target
for(let i = 0; i < len - 3; i++) {// 去重iif(i > 0 && nums[i] === nums[i - 1]) continue;单调栈：（单调递增/减）下/上一个更大/小元素
输入一个数组 nums，请你返回一个等长的结果数组，结果数组中对应索引存储着下一个更大元素，如果没有更大的元素，就存 -1
nums = [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。因为第一个 2 后面比 2 大的数是 4; 1 后面比 1 大的数是 2；第二个 2 后面比 2 大的数是 4; 4 后面没有比 4 大的数，填 -1；3 后面没有比 3 大的数，填 -1。
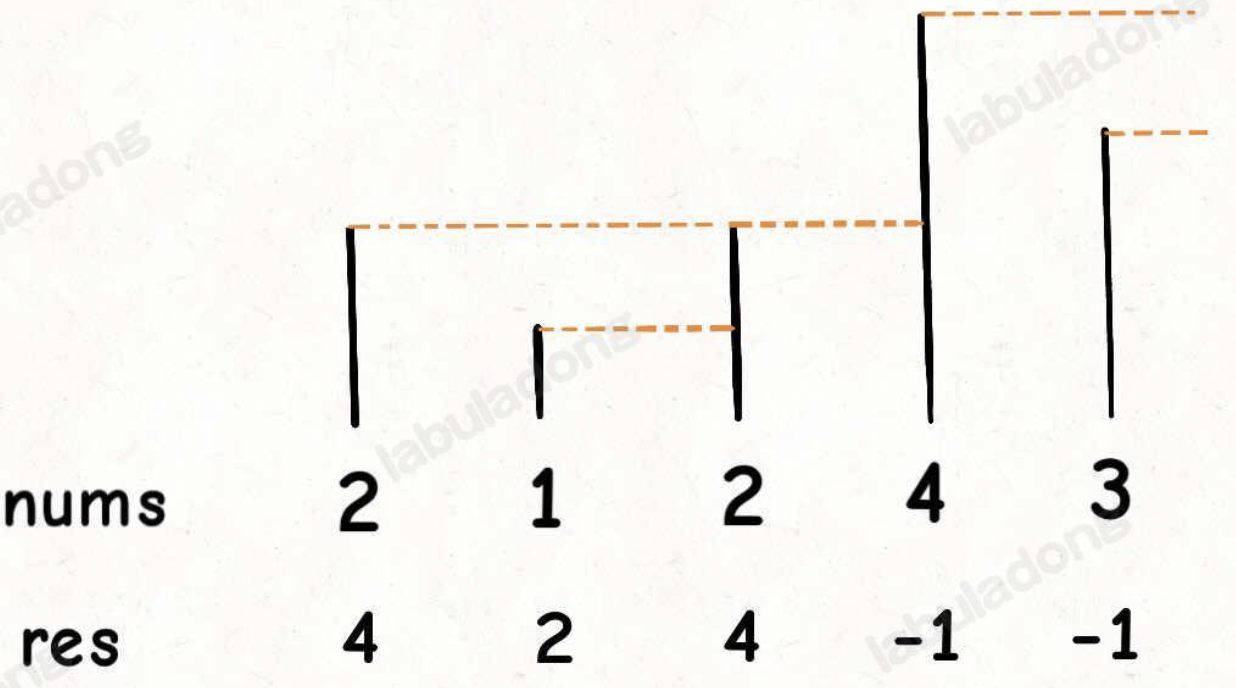
var nextGreaterElement = function(nums) {var n = nums.length;// 存放答案的数组var res = new Array(n).fill(0);var s = []; for (var i = n - 1; i >= 0; i--) {// 判定个子高矮while (s.length && s[s.length - 1] <= nums[i]) {// 矮个起开，反正也被挡着了。。。s.pop();}// nums[i] 身后的更大元素res[i] = s.length ? s[s.length - 1] : -1;// 倒着往栈里放s.push(nums[i]);}return res;
};
二叉树
(反)序列化二叉树：先序
序列化二叉树，key：
- let arr = Array.isArray(s) ? s : s.split("");
- let a = arr.shift();
- let node = null;
- if (typeof a === "number")
function TreeNode(x) {this.val = x;this.left = null;this.right = null;
}
//反序列化二叉树：tree->str 把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串
function Serialize(pRoot, arr = []) {if (!pRoot) {arr.push("#");return arr;} else {arr.push(pRoot.val);//注意是val。而不是rootSerialize(pRoot.left, arr);Serialize(pRoot.right, arr);}return arr;
}
//序列化二叉树：str->tree 根据字符串结果str，重构二叉树
function Deserialize(s) {//转换为数组let arr = Array.isArray(s) ? s : s.split("");//取出vallet a = arr.shift();//构建二叉树结点let node = null;if (typeof a === "number") {//还有可能等于#node = new TreeNode(a);node.left = Deserialize(arr);node.right = Deserialize(arr);}return node;
}
module.exports = {Serialize: Serialize,Deserialize: Deserialize,
};
前序遍历（迭代）/路径
stack.length
入栈：中右左
出栈：中左右
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number[]}*/
var preorderTraversal = function(root) {let stack=[]let res = []let cur = null;if(!root) return res;root&&stack.push(root)while(stack.length){cur = stack.pop()res.push(cur.val)cur.right&&stack.push(cur.right)cur.left&&stack.push(cur.left)}return res
};
中序遍历（迭代）
cur||stack.length
指针的遍历来帮助访问节点，栈则用来处理节点上的元素
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number[]}*/
var inorderTraversal = function(root) {let stack = []let res = []let cur = rootwhile(cur||stack.length){if(cur){stack.push(cur)cur = cur.left} else {cur = stack.pop()res.push(cur.val)cur = cur.right}}return res
};
后序遍历（迭代）
和前序遍历不同：
入栈：中左右
出栈：中右左
reverse出栈：左右中
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number[]}*/
var postorderTraversal = function(root) {let stack = []let res = []let cur = rootif(!root) return resstack.push(root)while(stack.length){cur = stack.pop()res.push(cur.val)cur.left&&stack.push(cur.left)cur.right&&stack.push(cur.right)}return res.reverse()};
层序遍历：深度
树的层序遍历，相似 图的广度优先搜索
- 初始设置一个空队，根结点入队
- 队首结点出队，其左右孩子 依次 入队
- 若队空，说明 所有结点 已处理完，结束遍历；否则（2)
/** function TreeNode(x) {* this.val = x;* this.left = null;* this.right = null;* }*//**** @param root TreeNode类* @return int整型二维数组*/
function levelOrder(root) {// write code hereif (root == null) {return [];}const arr = [];const queue = [];queue.push(root);while (queue.length) {const preSize = queue.length;const floor = [];//当前层for (let i = 0; i < preSize; ++i) {const v = queue.shift();floor.push(v.val);v.left&&queue.push(v.left);v.right&&queue.push(v.right);}arr.push(floor);}return arr;//[[1],[2,3]]
}
module.exports = {levelOrder: levelOrder,
};
判断完全二叉树
queue.length
flag = false; //是否遇到空节点
完全二叉树：叶子节点只能出现在最下层和次下层，且最下层的叶子节点集中在树的左部。
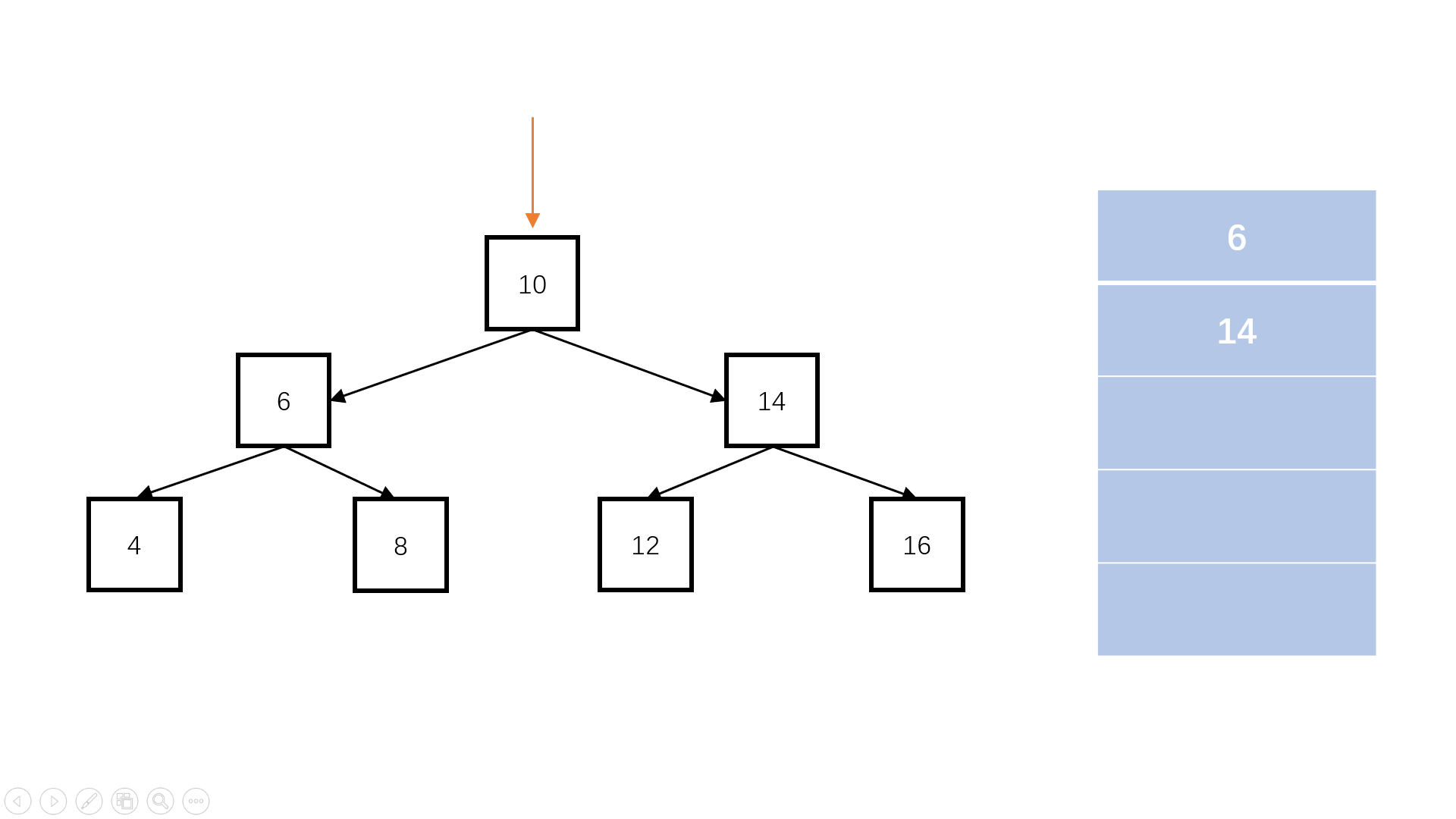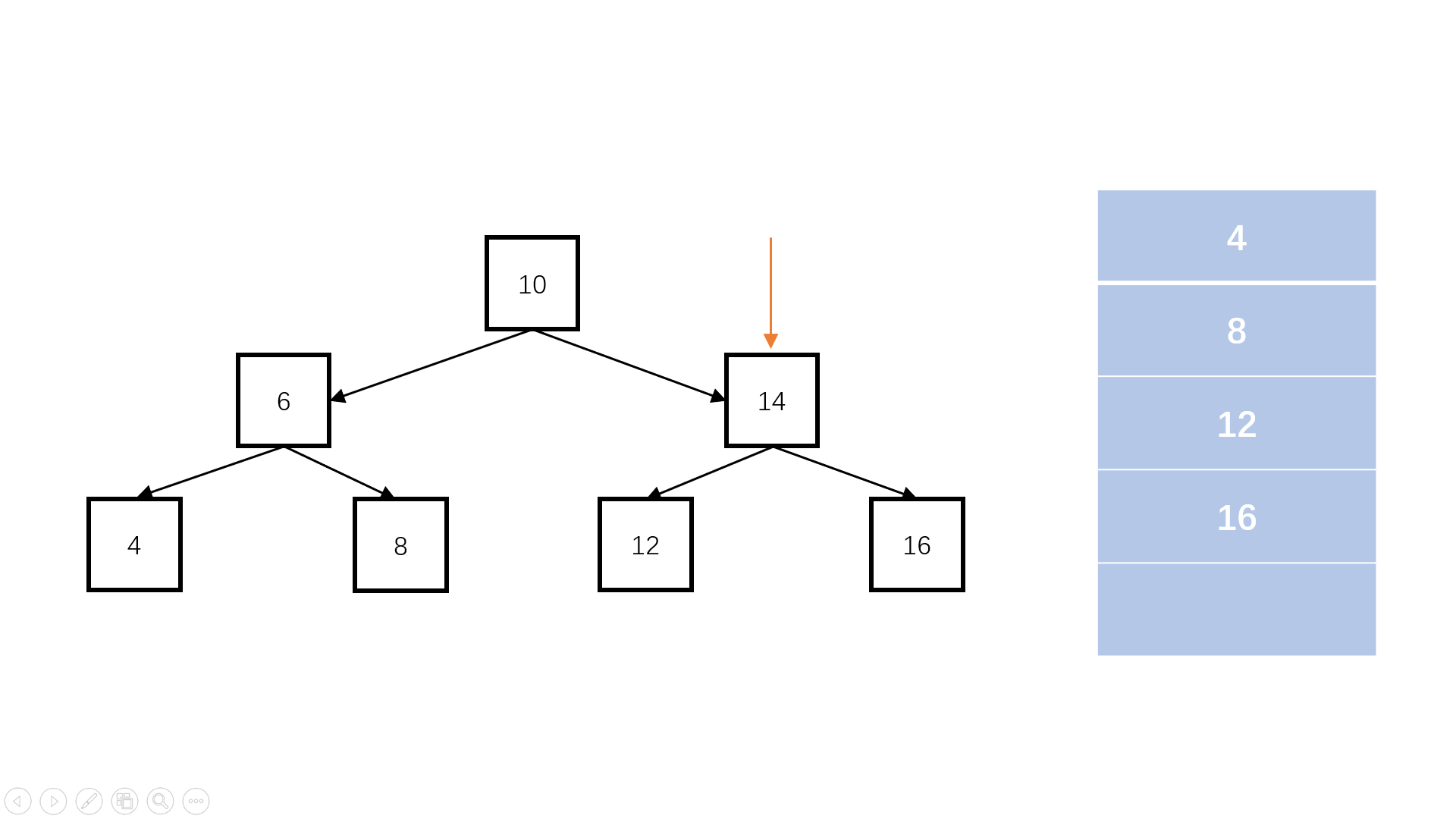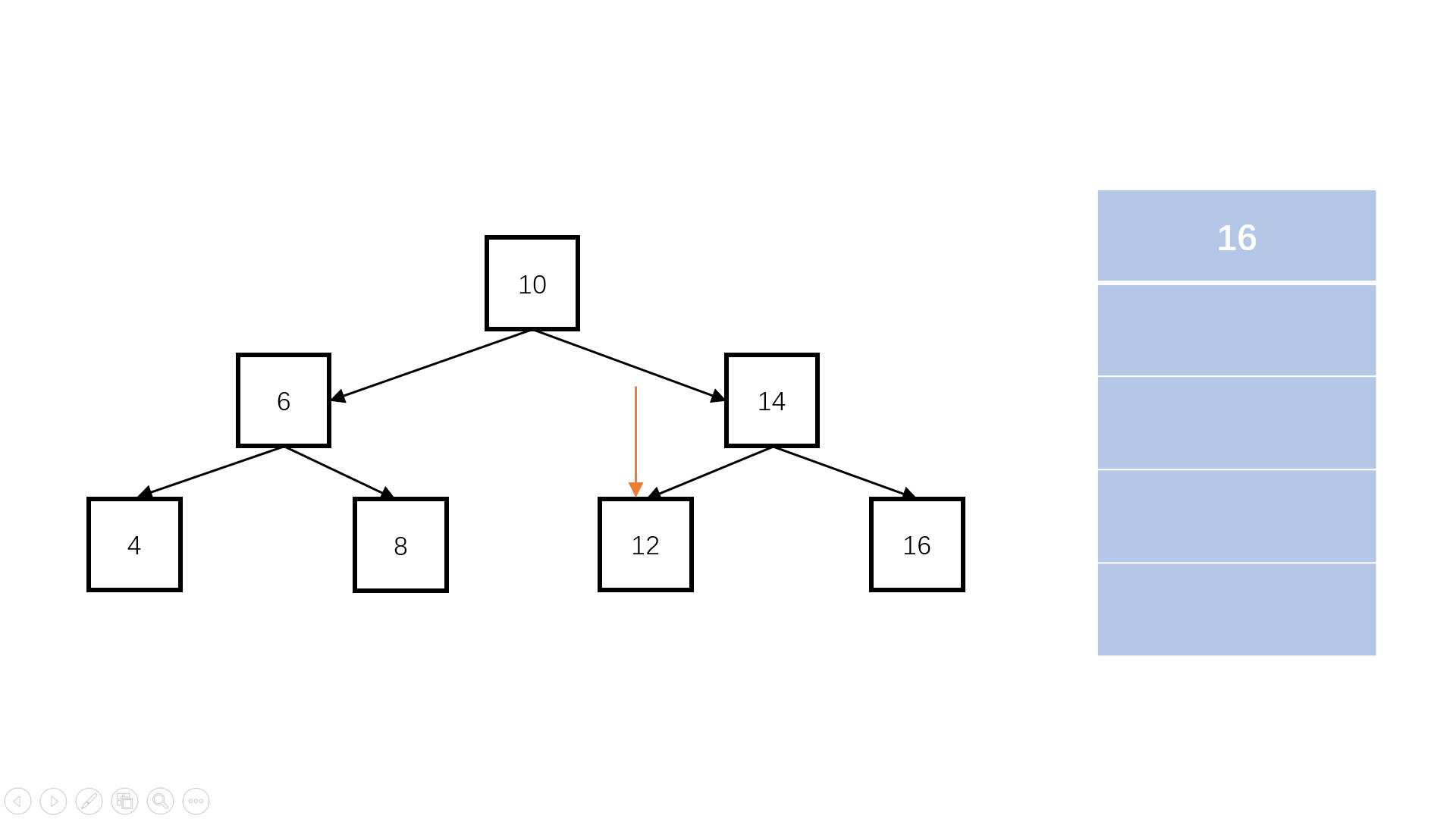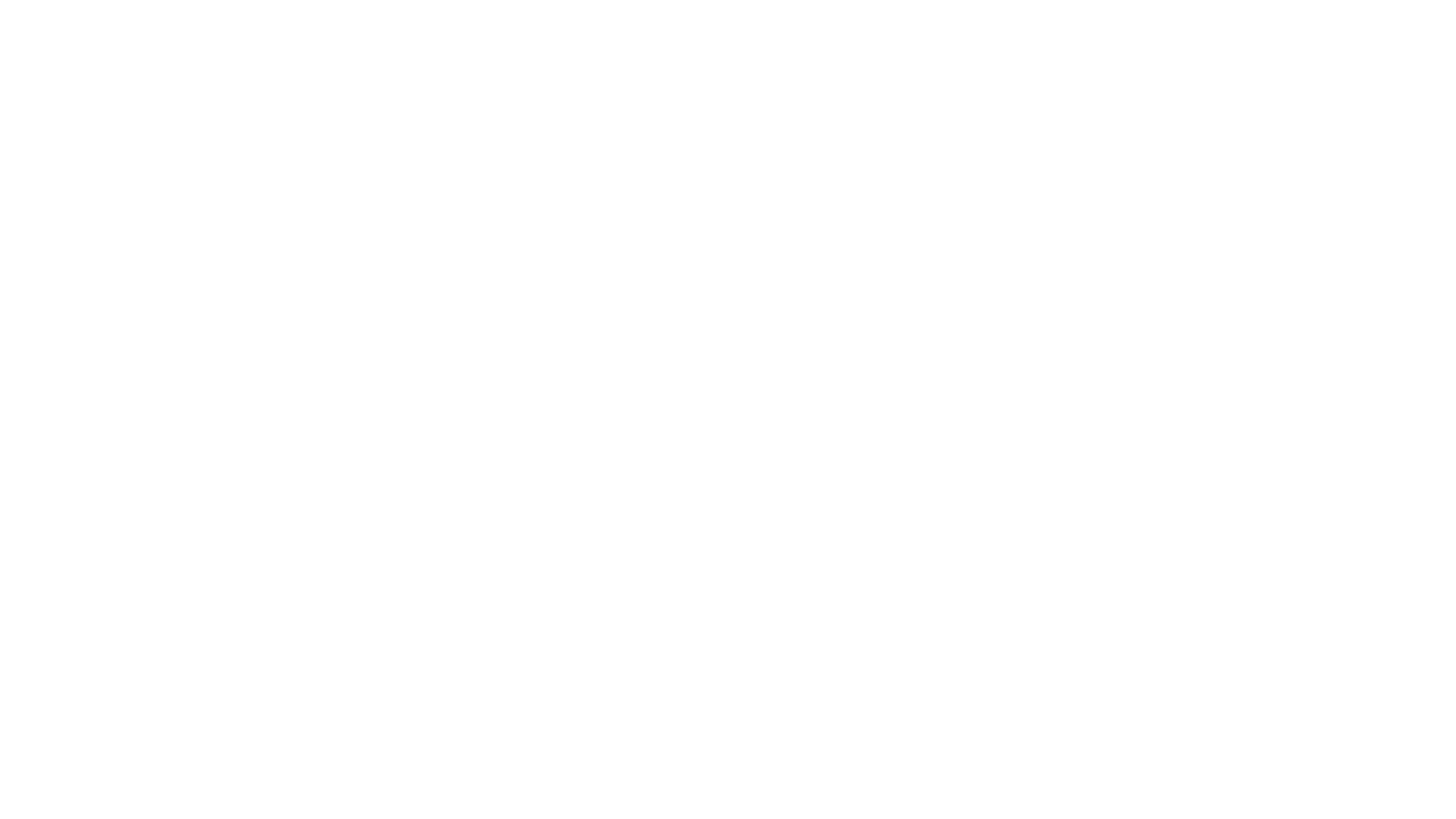
/** function TreeNode(x) {* this.val = x;* this.left = null;* this.right = null;* }*/
/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可*** @param root TreeNode类* @return bool布尔型*/
function isCompleteTree(root) {// write code hereif (root == null) return true;const queue = [];queue.push(root);let flag = false; //是否遇到空节点while (queue.length) {const node = queue.shift();if (node == null) {//如果遇到某个节点为空，进行标记，代表到了完全二叉树的最下层flag = true;continue;}if (flag == true) {//若是后续还有访问，则说明提前出现了叶子节点，不符合完全二叉树的性质。return false;}queue.push(node.left);queue.push(node.right);}return true;
}
module.exports = {isCompleteTree: isCompleteTree,
};
判断平衡二叉树
平衡二叉树是左子树的高度与右子树的高度差的绝对值小于等于1，同样左子树是平衡二叉树，右子树为平衡二叉树。
递归Math.max(getMaxDepth(root.left)+1,getMaxDepth(root.right)+1)
/* function TreeNode(x) {this.val = x;this.left = null;this.right = null;
} */
function IsBalanced_Solution(pRoot)
{if(!pRoot) return true;// write code herereturn (Math.abs(getMaxDepth(pRoot.left) - getMaxDepth(pRoot.right)) <=1) && IsBalanced_Solution(pRoot.left) && IsBalanced_Solution(pRoot.right)
}function getMaxDepth(root) {if(!root) return 0;return Math.max(getMaxDepth(root.left)+1,getMaxDepth(root.right)+1)
}
module.exports = {IsBalanced_Solution : IsBalanced_Solution
};判断对称二叉树
递归deep(left.left, right.right) && deep(left.right, right.left)
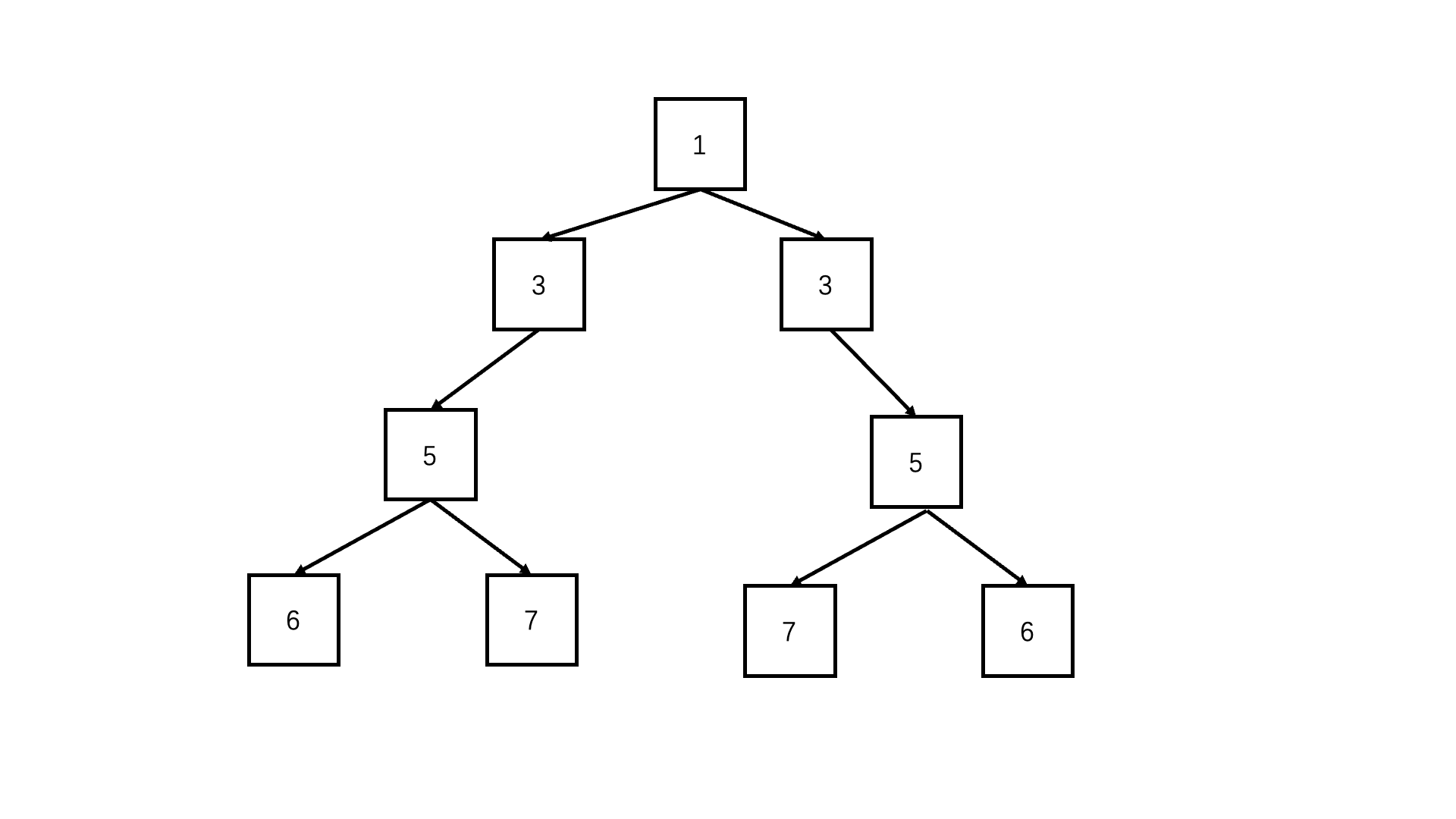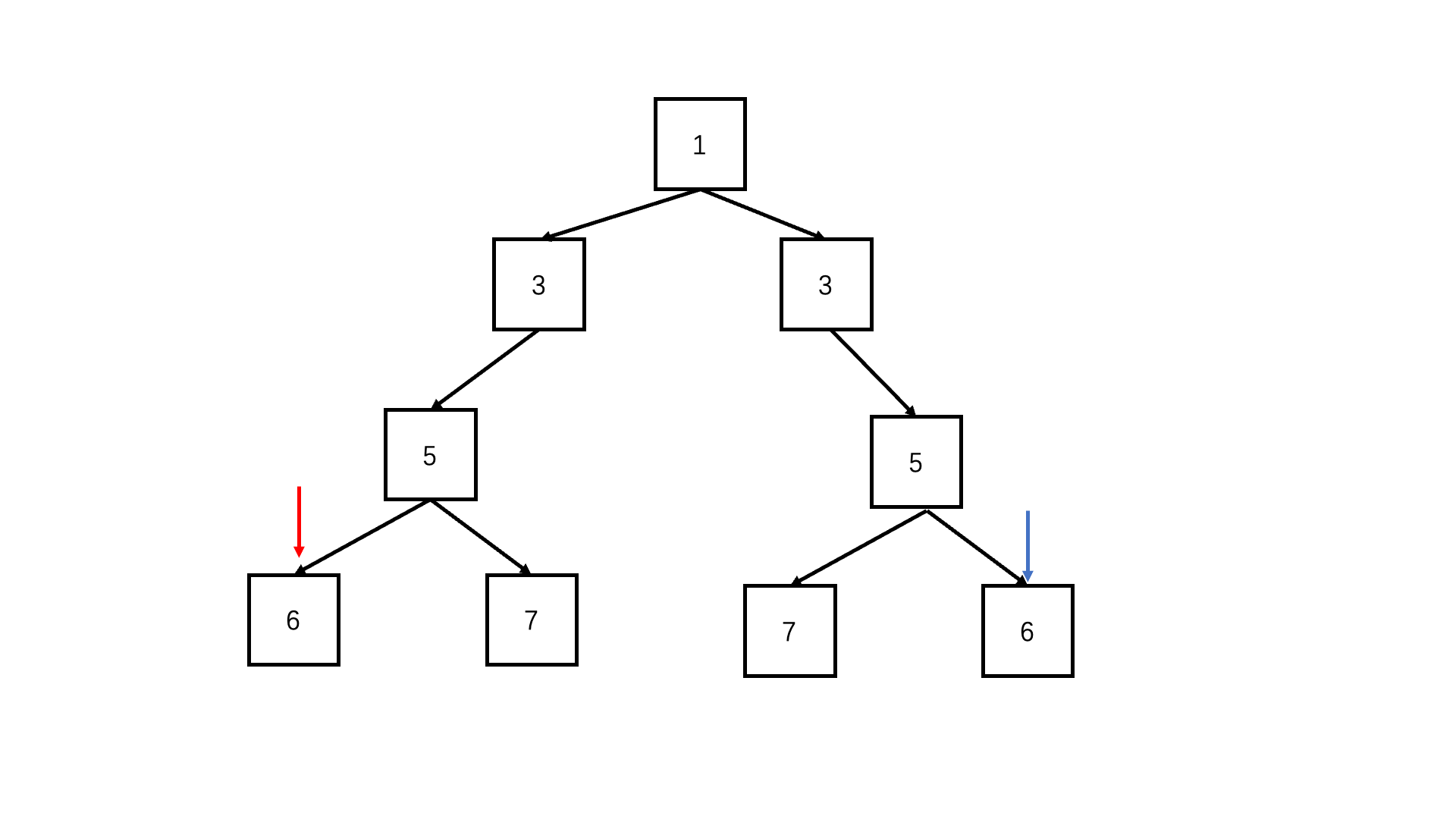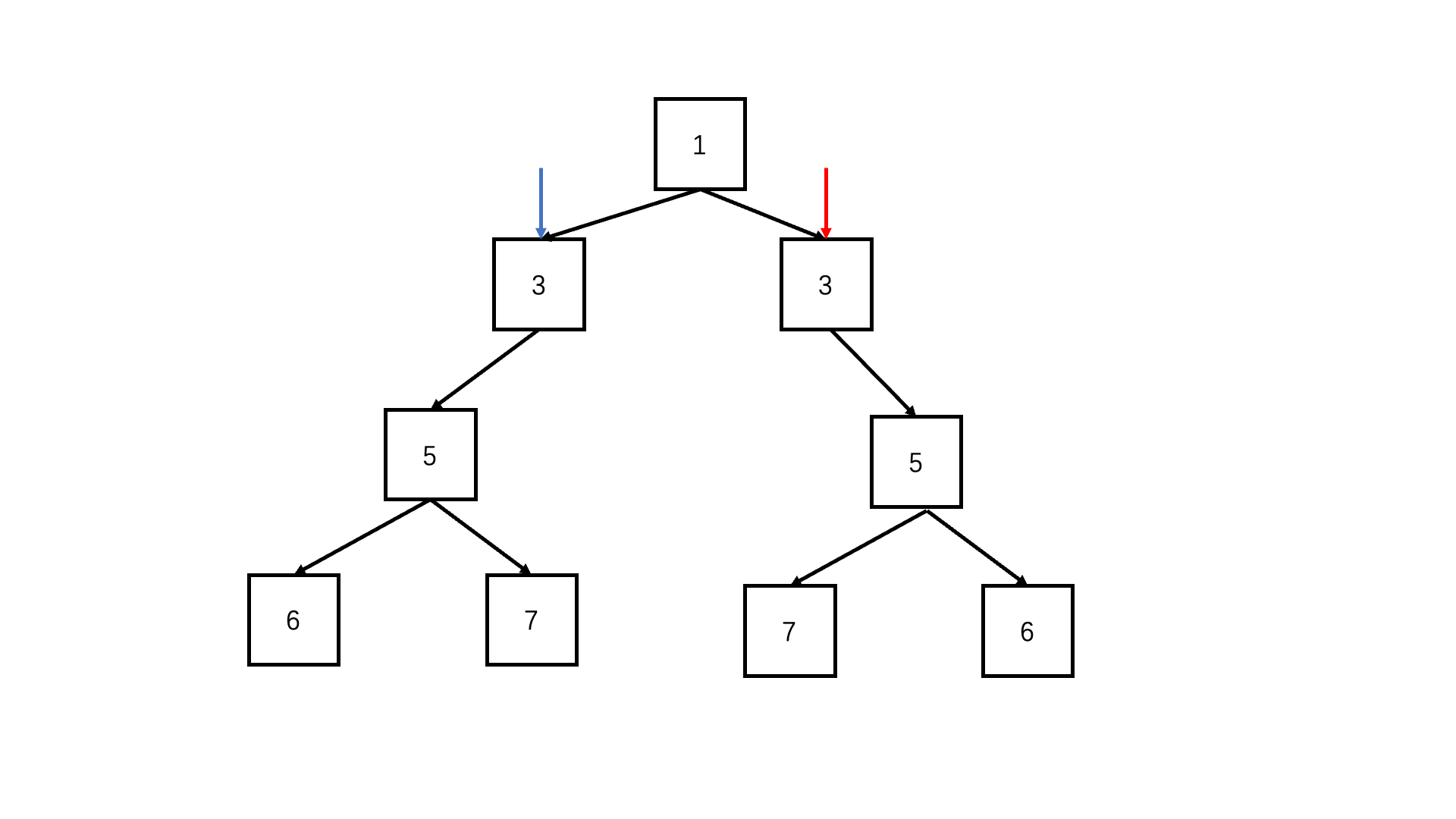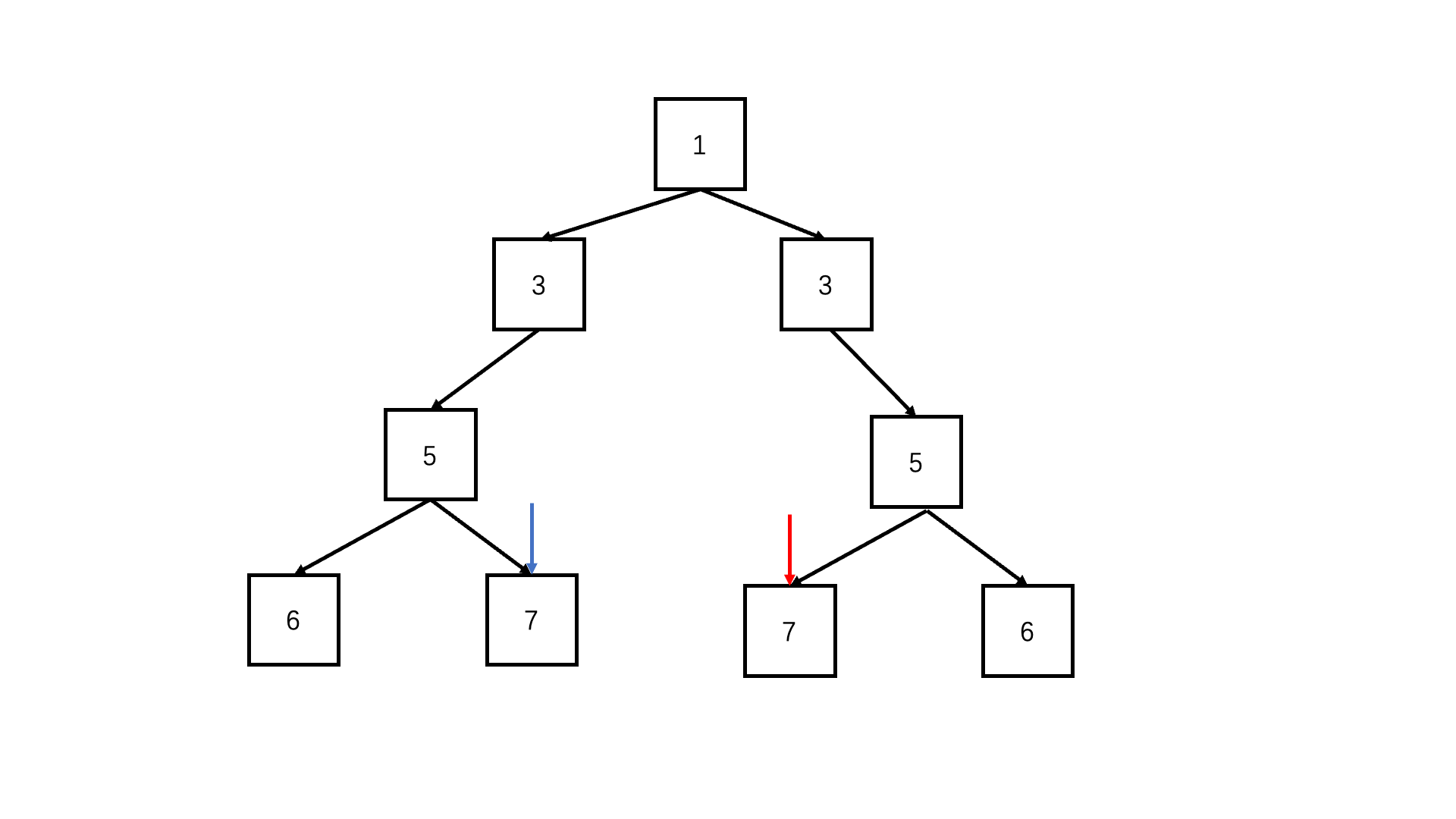
/* function TreeNode(x) {this.val = x;this.left = null;this.right = null;
} */
let flag = true;
function deep(left, right) {if (!left && !right) return true; //可以两个都为空if (!right||!left|| left.val !== right.val) {//只有一个为空或者节点值不同，必定不对称return false;}return deep(left.left, right.right) && deep(left.right, right.left); //每层对应的节点进入递归比较
}
function isSymmetrical(pRoot) {return deep(pRoot, pRoot);
}
module.exports = {isSymmetrical: isSymmetrical,
};
翻转/生成镜像二叉树
递归交换左右
先序遍历
/** function TreeNode(x) {* this.val = x;* this.left = null;* this.right = null;* }*/
/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param pRoot TreeNode类 * @return TreeNode类*/
function Mirror( pRoot ) {function traversal(root){if(root===null) return ;//交换左右孩子let temp = root.left;root.left = root.right;root.right = temp;traversal(root.left);traversal(root.right);return root;}return traversal(pRoot);// write code here
}
module.exports = {Mirror : Mirror
};两节点的最近公共祖先
如果从两个节点往上找，每个节点都往上走，一直走到根节点，那么根节点到这两个节点的连线肯定有相交的地方，
如果从上往下走，那么最后一次相交的节点就是他们的最近公共祖先节点。
递归后序遍历
/** function TreeNode(x) {* this.val = x;* this.left = null;* this.right = null;* }*//**** @param root TreeNode类* @param o1 int整型* @param o2 int整型* @return int整型*/
function dfs(root, o1, o2) {if (root == null || root.val == o1 || root.val == o2) {return root;}//递归遍历左子树let left = dfs(root.left, o1, o2);//递归遍历右子树let right = dfs(root.right, o1, o2);//如果left、right都不为空，那么代表o1、o2在root的两侧，所以root为他们的公共祖先if (left && right) return root;//如果left、right有一个为空，那么就返回不为空的那一个return left != null ? left : right;
}东哥带你刷二叉树（思路篇） | labuladong 的算法小抄
数组和树
扁平结构(一维数组)转树
obj[item.id] = { ...item, children: [] }
pid === 0
!obj[pid]
obj[pid].children.push(treeitem)
//pid：parent id let arr = [{ id: 1, name: '部门1', pid: 0 },{ id: 2, name: '部门2', pid: 1 },{ id: 3, name: '部门3', pid: 1 },{ id: 4, name: '部门4', pid: 3 },{ id: 5, name: '部门5', pid: 4 },]// // 上面的数据转换为 下面的 tree 数据// [// {// "id": 1,// "name": "部门1",// "pid": 0,// "children": [// {// "id": 2,// "name": "部门2",// "pid": 1,// "children": []// },// {// "id": 3,// "name": "部门3",// "pid": 1,// "children": [// {// id: 4,// name: '部门4',// pid: 3,// "children": [// {// id: 5,// name: '部门5',// pid: 4,// "children": []// },// ]// },// ]// }// ]// }// ]function tree(items) {// 1、声明一个数组和一个对象 用来存储数据let arr = []let obj = {}// 2、给每条item添加children ，并连带一起放在obj对象里for (let item of items) {obj[item.id] = { ...item, children: [] }}// 3、for of 逻辑处理for (let item of items) {// 4、把数据里面的id 取出来赋值 方便下一步的操作let id = item.idlet pid = item.pid// 5、根据 id 将 obj 里面的每一项数据取出来let treeitem = obj[id]// 6、如果是第一项的话 吧treeitem 放到 arr 数组当中if (pid === 0) {// 把数据放到 arr 数组里面arr.push(treeitem)} else {// 如果没有 pid 找不到 就开一个 obj { }if (!obj[pid]) {obj = {children: []}}// 否则给它的 obj 根基 pid（自己定义的下标） 进行查找 它里面的children属性 然后pushobj[pid].children.push(treeitem)}}// 返回处理好的数据return arr}console.log(tree(arr))
数组扁平化
toString/join(',').split(',').map(Number)
要求将数组参数中的多维数组扩展为一维数组并返回该数组。
数组参数中仅包含数组类型和数字类型
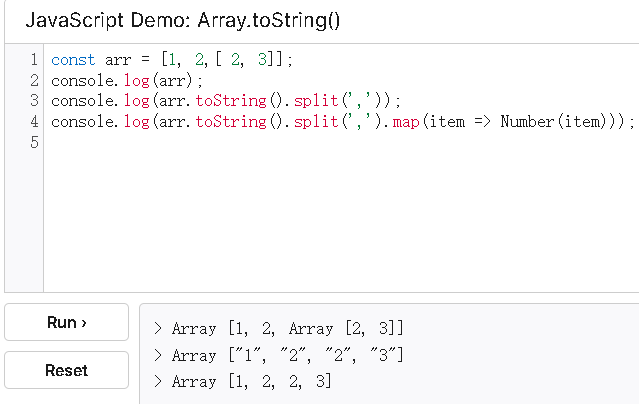
function flatten(arr){// toString() + split() 实现 return arr.toString().split(',').map(item => Number(item));//join() + split() 实现return arr.join(',').split(',').map(item => Number(item));//reduce 实现return arr.reduce((target, item) => {return target.concat(Array.isArray(item) ? flatten(item) : item);}, [])// 递归实现let res = [];arr.forEach(item => {if (Array.isArray(item)) {res = res.concat(flatten(item))} else {res.push(item);}});return res;// 扩展运算符实现while(arr.some(item => Array.isArray(item))){arr = [].concat(...arr);}return arr;// flat()实现（这里不支持使用）return arr.flat(Infinity);
}排序
快速排序
快速排序的基本思想是通过分治来使一部分均比另一部分小（大）再使两部分重复该步骤而实现有序的排列。核心步骤有：
- 选择一个基准值（pivot）
- 以基准值将数组分割为两部分
- 递归分割之后的数组直到数组为空或只有一个元素为止
key：
- pivot = array.splice(pivotIndex, 1)[0]
- _quickSort(left).concat([pivot], _quickSort(right))
const _quickSort = array => {if(array.length <= 1) return arrayvar pivotIndex = Math.floor(array.length / 2)var pivot = array.splice(pivotIndex, 1)[0]var left = []var right = []for (var i=0 ; iBFS：最短路径
BFS 找到的路径一定是最短的，但代价就是空间复杂度可能比 DFS 大很多
回溯O(N!)：选择/DFS
如果不能成功，那么返回的时候我们就还要把这个位置还原。这就是回溯算法，也是试探算法。
解决一个回溯问题，实际上就是一个决策树的遍历过程。
1、路径：已选择。
2、选择列表：可选择。
3、结束条件：无选择。
框架：排列/组合/子集
result = []
function backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择全排列中
做选择/撤销选择 可用if(path.includes(item)) continue;代替元素无重不可复选
全排列
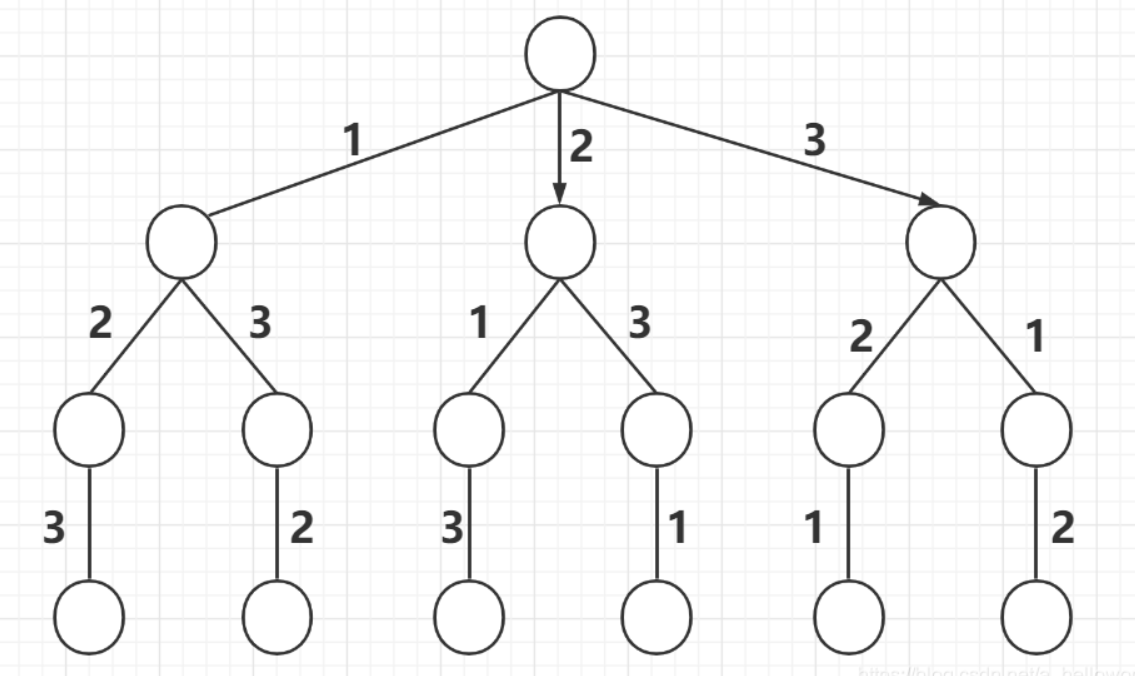
key：
- path.length == string.length
- path.includes(item)
const _permute = string => {const res = [];const backtrace = path => {if(path.length == string.length){res.push(path);return;}for(const item of string) {if(path.includes(item)) continue;backtrace(path + item);}};backtrace('');return res;
}子集
输入一个无重复元素的数组 nums，其中每个元素最多使用一次，请你返回 nums 的所有子集
比如输入 nums = [1,2,3]，算法应该返回如下子集：
[ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]
/*** @param {number[]} nums* @return {number[][]}*/
var subsets = function(nums) {// 用于存储结果const res = [];// 用于记录回溯路径const track = [];/*** 回溯算法的核心函数，用于遍历子集问题的回溯树* @param {number} start - 控制树枝的遍历，避免产生重复子集*/const backtrack = (start) => {// 前序遍历位置，每个节点的值都是一个子集res.push([...track]);// 回溯算法标准框架for (let i = start; i < nums.length; i++) {// 做选择track.push(nums[i]);// 回溯遍历下一层节点backtrack(i + 1);// 撤销选择track.pop();}};backtrack(0);return res;
};元素无重不可复选：排序，多条值相同的只遍历第一条
子集/组合
nums = [1,2,2]，你应该输出：
[ [],[1],[2],[1,2],[2,2],[1,2,2] ]如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历：
先进行排序，让相同的元素靠在一起，如果发现 nums[i] == nums[i-1]，则跳过
排列
// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码还未经过力扣测试，仅供参考，如有疑惑，可以参照我写的 java 代码对比查看。/*** @param {number[]} nums* @return {number[][]}*/var permuteUnique = function(nums) {let res = [];let track = [];let used = new Array(nums.length).fill(false);// 先排序，让相同的元素靠在一起nums.sort((a, b) => a - b);backtrack(nums, used, track, res);return res;
};/*** @param {number[]} nums* @param {boolean[]} used* @param {number[]} track* @param {number[][]} res*/
function backtrack(nums, used, track, res) {if (track.length === nums.length) {res.push(track.slice());return;}for (let i = 0; i < nums.length; i++) {if (used[i]) {continue;}// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {continue;}track.push(nums[i]);used[i] = true;backtrack(nums, used, track, res);track.pop();used[i] = false;}
}
元素无重可复选
子集/组合：sum=target
想让每个元素被重复使用，我只要把 i + 1 改成 i 即可
给之前的回溯树添加了一条树枝，在遍历这棵树的过程中，一个元素可以被无限次使用
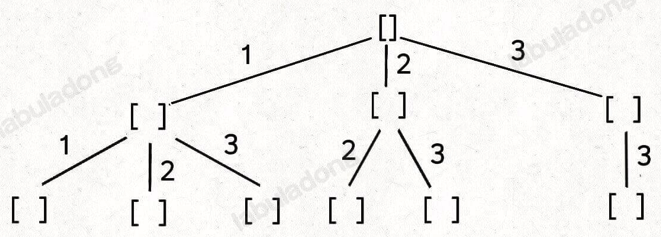
这棵回溯树会永远生长下去，所以我们的递归函数需要设置合适的 base case 以结束算法，即路径和大于 target 时就没必要再遍历下去了
排列：去除 used 剪枝
N皇后
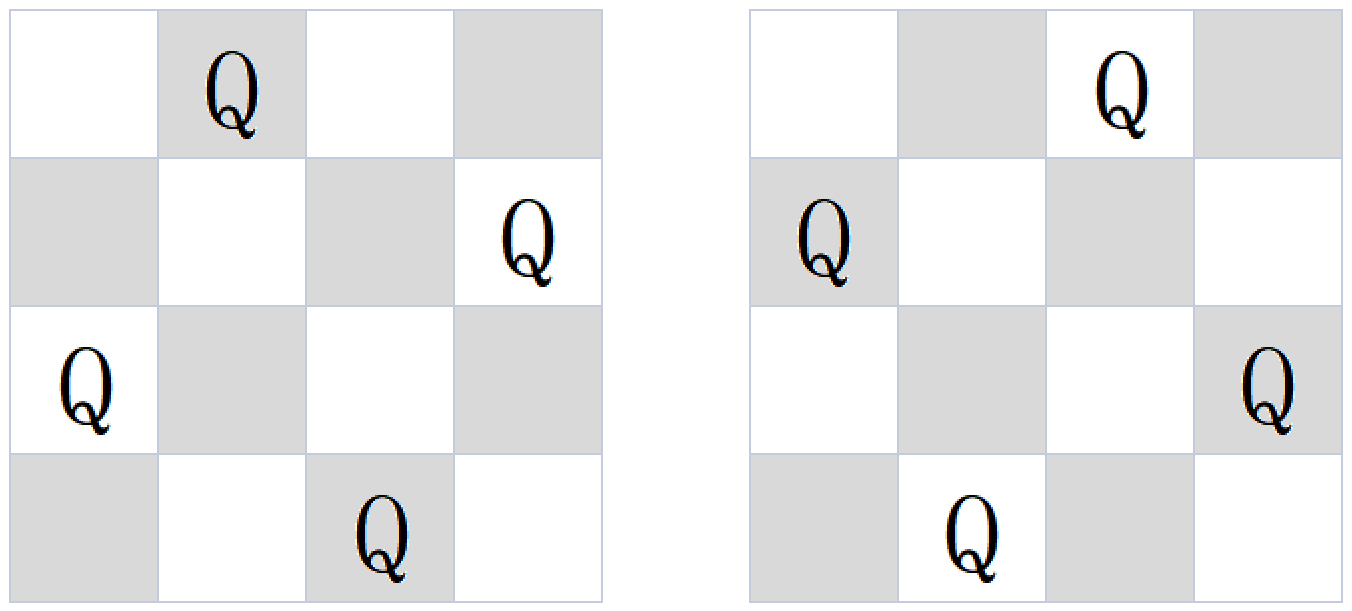
在 n * n 的棋盘上要摆 n 个皇后，
要求：任何两个皇后不同行，不同列也不在同一条斜线上，
求给一个整数 n ，返回 n 皇后的摆法数。
要求：空间复杂度 O(1) ，时间复杂度O(n!)
- 要确定皇后的位置，其实就是确定列的位置，因为行已经固定了
- 进一步讲，也就是如何摆放 数组
arr[0,1,2,3,...,n-1] - 如果没有【不在同一条斜线上】要求，这题其实只是单纯的全排列问题
- 在全排列的基础上，根据N皇后的问题，去除一些结果
-
arr：n个皇后的列位置 -
res：n皇后排列结果 -
ruler：记录对应的列位置是否已经占用（也是是否有皇后），如果有，那么设为1，没有设为0 -
setPos：哈希集合，标记正斜线（从左上到右下）位置，如果在相同正斜线上，坐标(x,y)满足 y-x 都相同，(y1 - x1)应该等于(y2 - x2)。 -
setCon：哈希集合，标记反正斜线（从y右上到左下）位置，如果在相同反斜线上，坐标(x,y)满足 x+y 都相同，(x1 + y1)应该等于(x2 + y2)。 -
是否在同一斜线上，其实就是这两个点的所形成的斜线的斜率是否为±1。点P(a,b) ，点Q(c,d)
（1）斜率为1 (d-b)/(c-a) = 1，横纵坐标之差相等
（2）斜率为-1 (d-b)/(c-a) = -1 ，等式两边恒等变形 a+b = c + d ，横纵坐标之和相等
/**** @param n int整型 the n* @return int整型*/
function Nqueen(n) {let res = []; //二维数组，存放每行Q的列坐标let isQ = new Array(n).fill(0); //记录该列是否有Qlet setPos = new Set(); //标记正对角线let setCon = new Set(); // 标记反对角线//给当前row找一个colconst backTrace = (row, path) => {if (path.length === n) {res.push(path);return;}for (let col = 0; col < n; col++) {if (isQ[col] == 0 &&!setPos.has(row - col) &&!setCon.has(row + col)) {path.push(col);isQ[col] = 1;setPos.add(row - col);setCon.add(row + col);backTrace(row + 1, path);path.pop();isQ[col] = 0;setPos.delete(row - col);setCon.delete(row + col);}}};backTrace(0, []);return res.length;
}
module.exports = {Nqueen: Nqueen,
};
动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质，可以用 dp table 或者备忘录优化，将递归树大幅剪枝，这就变成了动态规划。
动态规划(Dynamic Programming，DP) 最值选择+重叠子问题
输入（i，j，w）：for(i，j){w}
分解为简单的子问题
递归或者递推的写法来实现动态规划，其中递归写法在此处又称作记忆化搜索。
一维输入+一维dp：斐波那契(Fibonacci）数列（递归）
function F(n){
if(n= 0||n== 1) return 1;
else return F(n-1)+F(n-2);
}
dp[n]=-1表示F(n)当前还没有被计算过
function F(n) {
if(n == 0||n==1) return 1;//递归边界
if(dp[n] != -1) return dp[n]; //已经计算过，直接返回结果，不再重复计算else {
else dp[n] = F(n-1) + F(n-2); //计算F(n)，并保存至dp[n]
return dp [n];//返回F(n)的结果
}
数塔（递推）
第i层有i个数字。现在要从第一层走到第n层，最后将路径上所有数字相加后得到的和最大是多少?
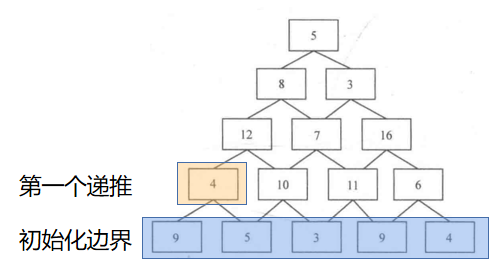
dp[i][j]表示从第i行第j个数字出发到达最底层的所有路径中能得到的最大和
dp[i][i]=max(dp[i-1][j],dp[i-1][j+1])+f[i][j]
二维输入+二维dp：for(输入)
最长公共子序列(LCS)
Longest Common Subsequence：子序列可以不连续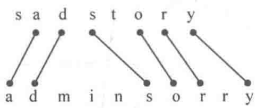
“sadstory”与“adminsorry”最长公共子序列为“adsory”
dp[i][j]：strA[i]和strB[j]之前的LCS 长度，下标从1开始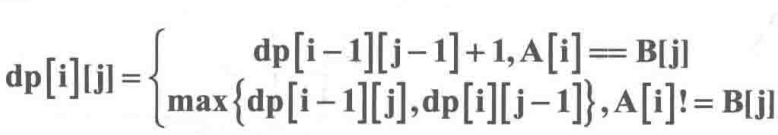
一维输入->start+end(二维)+二维dp：for(输入)
最长回文子串
dp[i][j]表示S[i]至S[j]所表示的子串是否是回文子串，是则为1，不是为0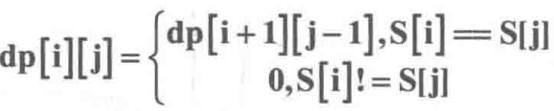
最小路径和
mxn矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。
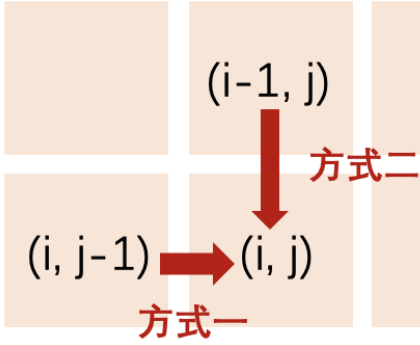dp[i][j]代表i到j的最短路径
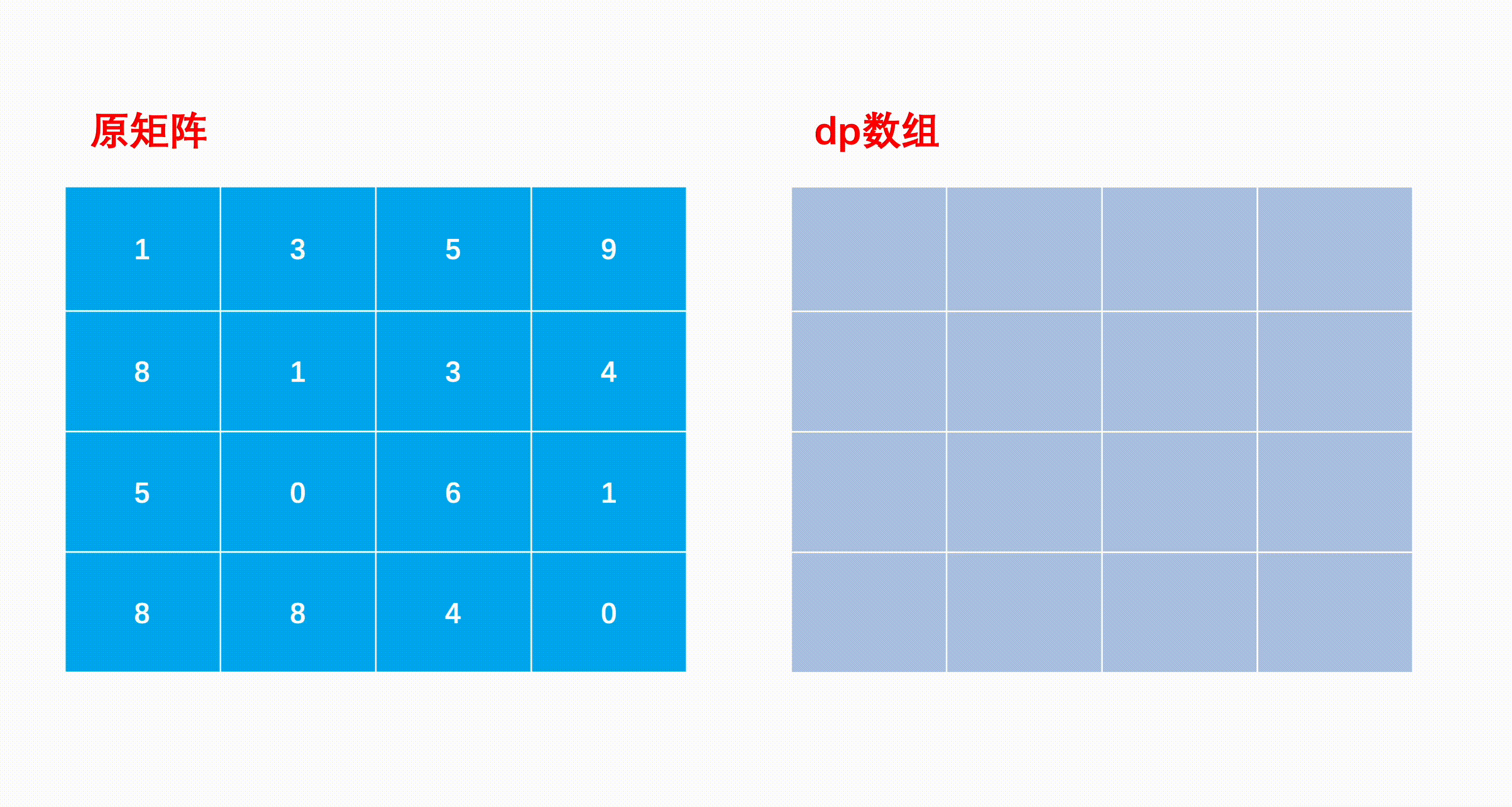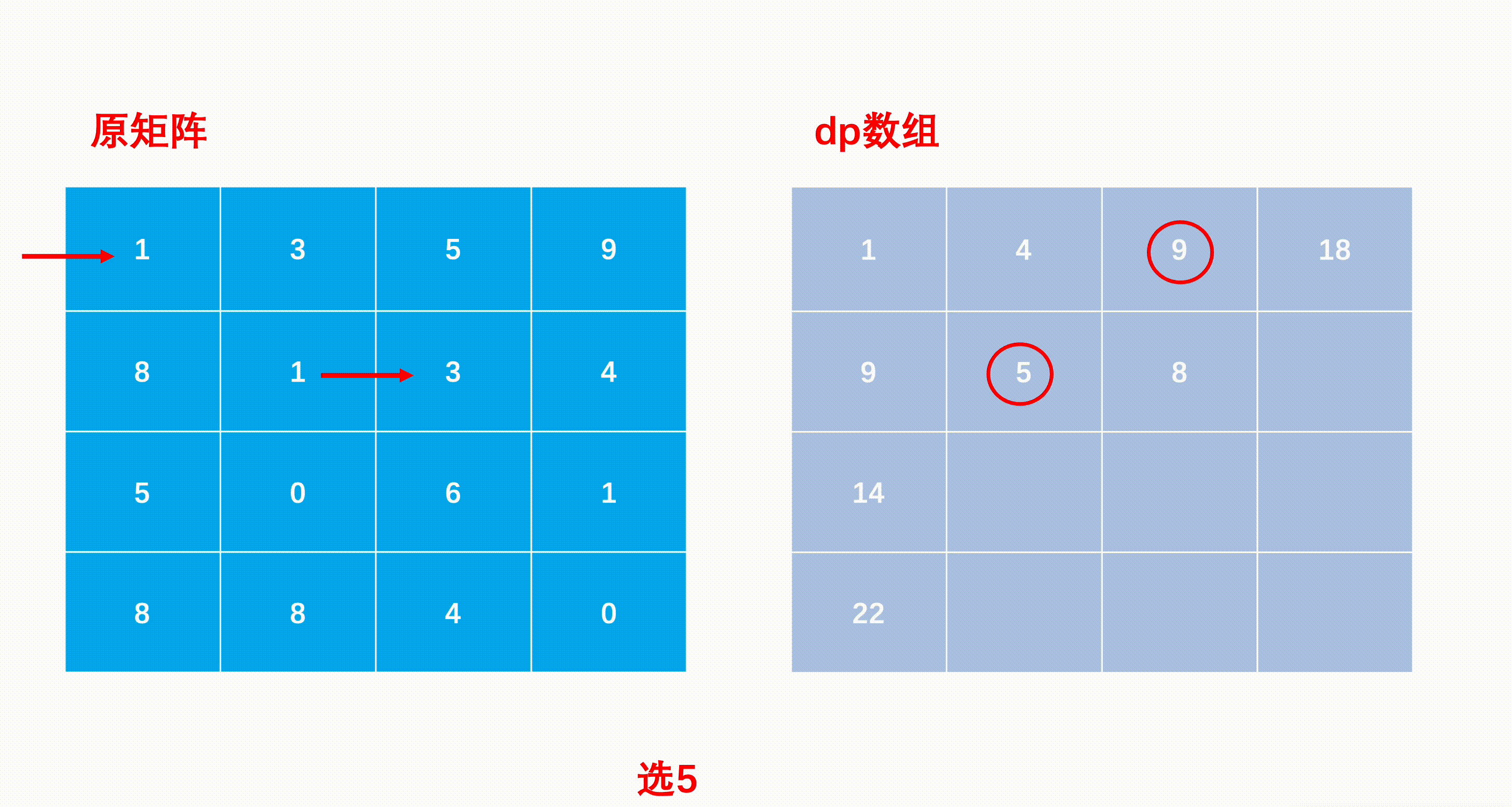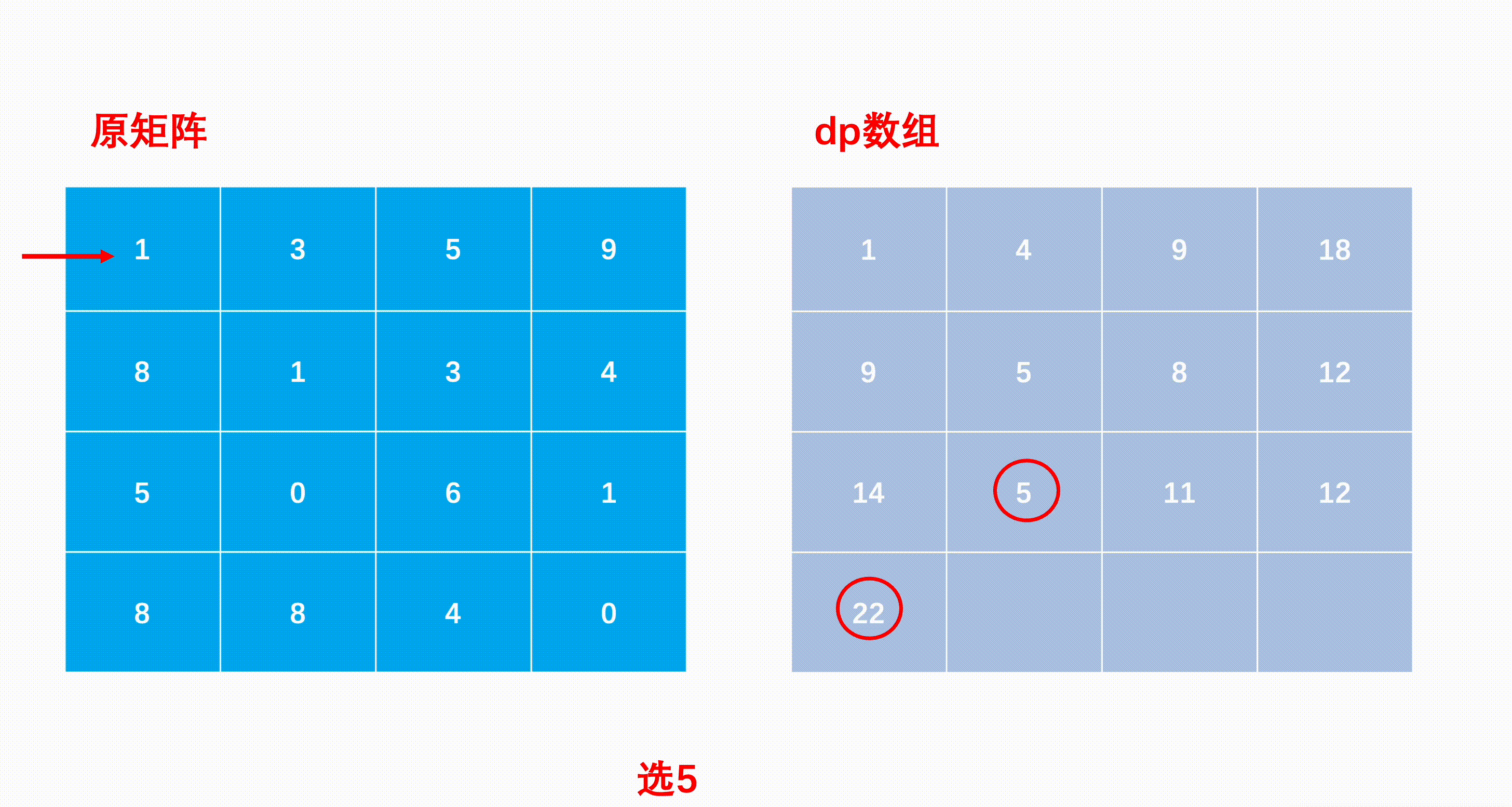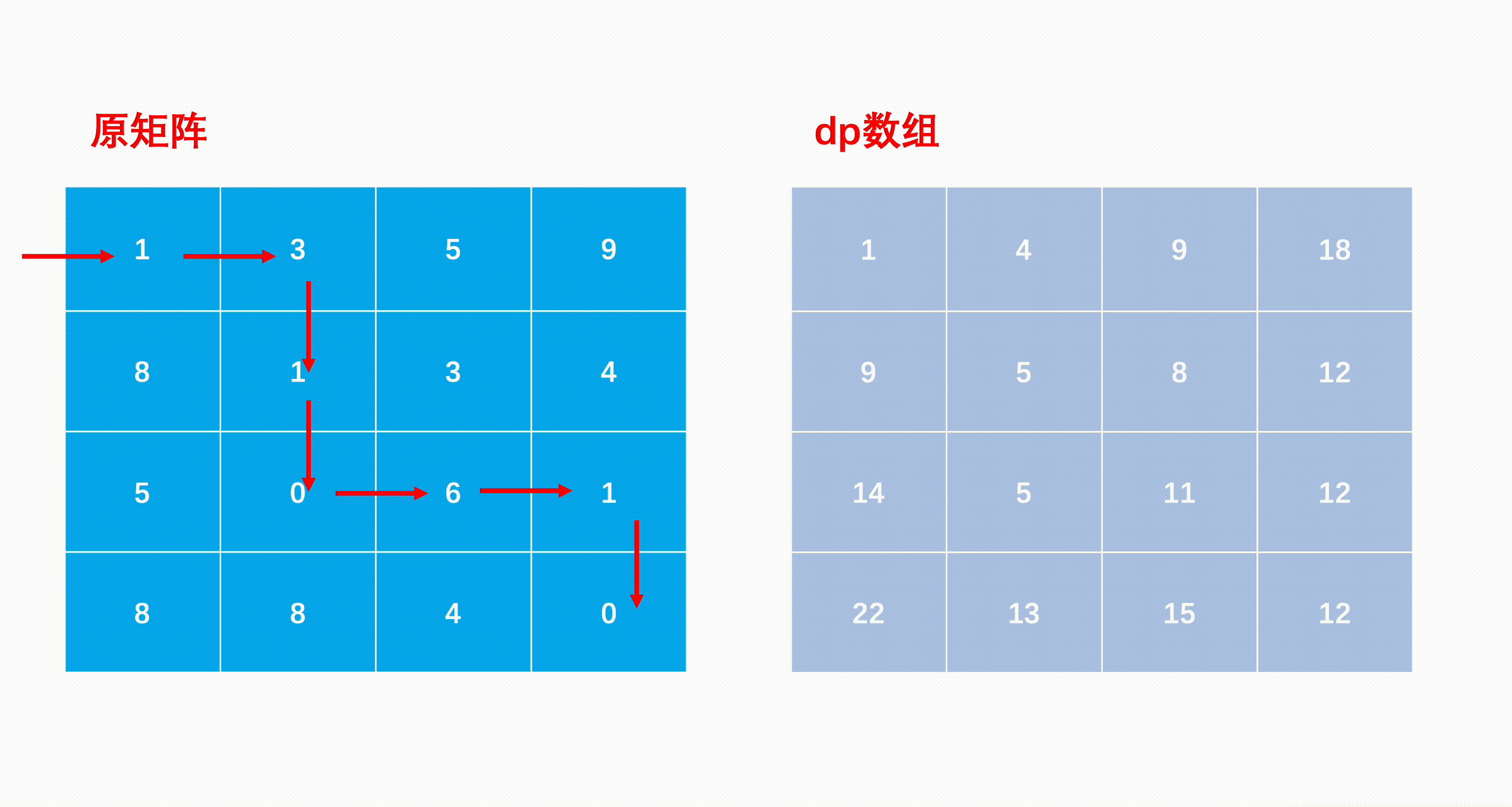
求解子问题时的状态转移方程：从「上一状态」到「下一状态」的递推式。
dp[i, j] = min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j]
JavaScript中没有二维数组的概念，但是可以设置 数组元素的值 等于 数组
key：
- dp[0][i] = dp[0][i - 1] + matrix[0][i];
- dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];
function minPathSum(matrix) {var row = matrix.length,col = matrix[0].length;var dp = new Array(row).fill(null).map(() => new Array(col).fill(0));dp[0][0] = matrix[0][0]; // 初始化左上角元素// 初始化第一行for (var i = 1; i < col; i++) dp[0][i] = dp[0][i - 1] + matrix[0][i];// 初始化第一列for (var j = 1; j < row; j++) dp[j][0] = dp[j - 1][0] + matrix[j][0];// 动态规划for (var i = 1; i < row; i++) {for (var j = 1; j < col; j++) {dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];}}return dp[row - 1][col - 1]; // 右下角元素结果即为答案
}二维/多维输入+限制条件v/h+二维/多维dp：for(输入)for(限制)
背包
框架
for 状态1 in 状态1的所有取值：for 状态2 in 状态2的所有取值：for ...dp[状态1][状态2][...] = 择优(选择1，选择2...)int dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0for i in [1..N]:for w in [1..W]:dp[i][w] = max(把物品 i 装进背包,不把物品 i 装进背包)
return dp[N][W]...加上边界条件，装不下的时候，只能选择不装01背包
n件物品,重量为w[i],价值为c[j]，容量为V的，其中每种物品都只有1件。
dp[i][v]表示前i件物品(1≤i≤n, 0≤v≤V)恰好装入容量为v的背包中所能获得的最大价值。
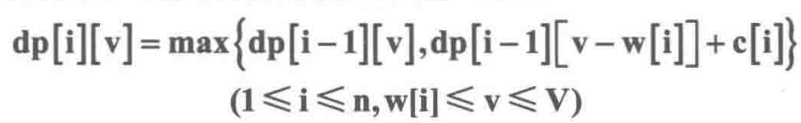
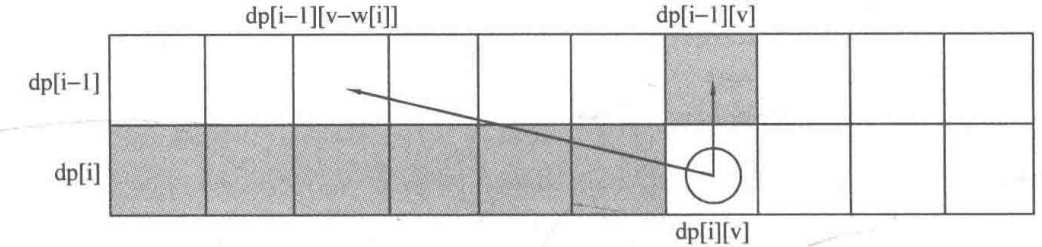
完全背包
与01背包问题不同的是其中每种物品都有无数件。
技巧
不用顺着题目思路来
输入的是一个单链表，让我分组翻转链表，而且还特别强调要用递归实现，就是我们旧文 K 个一组翻转链表 的算法。嗯，如果用数组进行翻转，两分钟就写出来了，嘿嘿。
还有我们前文 扁平化嵌套列表 讲到的题目，思路很巧妙，但是在笔试中遇到时，输入是一个形如 [1,[4,[6]]] 的字符串，那直接用正则表达式把数字抽出来，就是一个扁平化的列表了
输出为值（eg：Yes/No）
时间复杂度
logN，二分查找
MN，嵌套 for 循环/二维动态规划
数据规模
0 < n < 10，那很明显这个题目的复杂度很高，可能是指数或者阶乘级别的，因为数据规模再大一点它的判题系统就算不过来了嘛，这种题目十有八九就是回溯算法暴力穷举就完事。
一维数据：哈希/双指针/滑动窗口
树/图：遍历/递归（子树）
选择：回溯/动态规划/贪心
面试手撕
合法的URL
URL结构一般包括协议、主机名、主机端口、路径、请求信息、哈希
- 域名不区分大小写："www"子域名（可选）、二级域名、"com"顶级域名
- 只能包含字母（a-z、A-Z）、数字（0-9）和连字符（-）（但-不能再首尾）
https://www.bilibili.com/video/BV1F54y1N74E/?spm_id_from=333.337.search-card.all.click&vd_source=6fd32175adc98c97cd87300d3aed81ea
//开始: ^
//协议: http(s)?:\/\/
//域名: [a-zA-Z0-9]+-[a-zA-Z0-9]+|[a-zA-Z0-9]+
//顶级域名 如com cn,2-6位: [a-zA-Z]{2,6}
//端口 数字: (:\d+)?
//路径 任意字符 如 /login: (\/.+)?
//哈希 ? 和 # ，如?age=1: (\?.+)?(#.+)?
//结束: $
// https:// www.bilibili com /video/BV1F54y1N74E ?spm..
/^(http(s)?:\/\/)?(([a-zA-Z0-9]+-[a-zA-Z0-9]+|[a-zA-Z0-9]+)\.)+([a-zA-Z]{2,6})(:\d+)?(\/.+)?(\?.+)?(#.+)?$/.test(url)千位分割
const format = (n) => {let num = n.toString() // 拿到传进来的 number 数字 进行 toStringlet len = num.length // 在拿到字符串的长度// 当传进来的结果小于 3 也就是 千位还把结果返回出去 小于3 不足以分割if (len < 3) {return num} else {let render = len % 3 //传入 number 的长度 是否能被 3 整除if (render > 0) { // 说明不是3的整数倍return num.slice(0, render) + ',' + num.slice(render, len).match(/\d{3}/g).join(',')} else {return num.slice(0, len).match(/\d{3}/g).join(',')}}}let str = format(298000)console.log(str)
中序构建二叉树：递归
中序与后序遍历序列构造二叉树
从前序与中序遍历序列构造二叉树
常用方法/值
交换变量：[x,y]=[y,x]
Math/Number
//e=2.718281828459045
Math.E;//绝对值
Math.abs()//基数（base）的指数（exponent）次幂，即 base^exponent。
Math.pow(base, exponent)//max,min不支持传递数组
Math.max(value0, value1, /* … ,*/ valueN)
Math.max.apply(null,array)
//apply会将一个数组装换为一个参数接一个参数
//null是因为没有对象去调用这个方法,只需要用这个方法运算//取整
Math.floor() 向下取一个整数（floor地板）
Math.ceil() 向上取一个整数（ceil天花板）
Math.round() 返回一个四舍五入的值
Math.trunc() 直接去除小数点后面的值Number.MAX_VALUE
Number.MIN_VALUE;Map（set\delete\get\has\size）
保存键值对，
任何值（函数、对象、基本类型）都可以作为键/值。
object的键必须是一个String或是Symbol 。
const contacts = new Map()
contacts.set('Jessie', {phone: "213-555-1234", address: "123 N 1st Ave"})
contacts.has('Jessie') // true
contacts.get('Hilary') // undefined
contacts.delete('Jessie') // true
console.log(contacts.size) // 1function logMapElements(value, key, map) {console.log(`m[${key}] = ${value}`);
}new Map([['foo', 3], ['bar', {}], ['baz', undefined]]).forEach(logMapElements);// Expected output: "m[foo] = 3"
// Expected output: "m[bar] = [object Object]"
// Expected output: "m[baz] = undefined"
Set（add/delete/has/size）
值的集合，且值唯一
let setPos = new Set();
setPos.add(value);//Boolean
setPos.has(value);
setPos.delete(value);function logSetElements(value1, value2, set) {console.log(`s[${value1}] = ${value2}`);
}new Set(['foo', 'bar', undefined]).forEach(logSetElements);// Expected output: "s[foo] = foo"
// Expected output: "s[bar] = bar"
// Expected output: "s[undefined] = undefined"Array(join/splice/slice/indexOf/includes)
输出arr->srting：arr.join(separator) arr.toString()
初始化数组：new Array(length).fill(value)
增删：arr.(un)shift/pop/splice(start,delCnt,item...)
new Array(length).fill(0).map((_,idx)=> Number(idx))
arr.includes()
array.findIndex(item => item >30);
array.find(item => item> 30);
查询（时间复杂度和手动遍历一样）
//创建字符串
//join() 方法将一个数组（或一个类数组对象）的所有元素连接成一个字符串并返回这个字符串，
//用逗号或指定的分隔符字符串分隔。如果数组只有一个元素，那么将返回该元素而不使用分隔符。
Array.join()
Array.join(separator)//################创建数组：
//伪数组转成数组
Array.from(arrayLike, mapFn)
console.log(Array.from('foo'));
// Expected output: Array ["f", "o", "o"]console.log(Array.from([1, 2, 3], x => x + x));
// Expected output: Array [2, 4, 6]console.log( Array.from({length:3},(item, index)=> index) );// 列的位置
// Expected output:Array [0, 1, 2]//################原数组会改变：arr.reverse()//返回翻转后的数组// 无函数
//即升序
arr.sort()//默认排序顺序是在将元素转换为字符串，然后比较它们的 UTF-16
// 比较函数
arr.sort(compareFn)
function compareFn(a, b) {if (在某些排序规则中，a 小于 b) {return -1;}if (在这一排序规则下，a 大于 b) {return 1;}// a 一定等于 breturn 0;
}
//升序
function compareNumbers(a, b) {return a - b;
}//固定值填充
arr.fill(value)
arr.fill(value, start)
arr.fill(value, start, end)//去除
array.shift() //从数组中删除第一个元素，并返回该元素的值。array.pop() //从数组中删除最后一个元素，并返回该元素的值。
array.push() //将一个或多个元素添加到数组的末尾，并返回该数组的新长度//unshift() 方法将一个或多个元素添加到数组的开头，并返回该数组的新长度
array.unshift(element0, element1, /* … ,*/ elementN)//粘接，通过删除或替换现有元素或者原地添加新的元素来修改数组，并以数组形式返回被修改的内容。
array.splice(start)
array.splice(start, deleteCount)
array.splice(start, deleteCount, item1)
array.splice(start, deleteCount, item1, item2...itemN)//################原数组不会改变：//切片，浅拷贝（包括 begin，不包括end）。
array.slice()
array.slice(start)
array.slice(start, end)//展平，按照一个可指定的深度递归遍历数组，并将所有元素与遍历到的子数组中的元素合并为一个新数组返回。
array.flat()//不写参数默认一维
array.flat(depth)//过滤器，函数体 为 条件语句
// 箭头函数
filter((element) => { /* … */ } )
filter((element, index) => { /* … */ } )
filter((element, index, array) => { /* … */ } )
array.filter(str => str .length > 6) //遍历数组处理
// 箭头函数
map((element) => { /* … */ })
map((element, index) => { /* … */ })
map((element, index, array) => { /* … */ })
array.map(el => Math.pow(el,2))
//map和filter同参//接收一个函数作为累加器，数组中的每个值（从左到右）开始缩减，最终计算为一个值。
// 箭头函数
reduce((previousValue, currentValue) => { /* … */ } )
reduce((previousValue, currentValue, currentIndex) => { /* … */ } )
reduce((previousValue, currentValue, currentIndex, array) => { /* … */ } )
reduce((previousValue, currentValue) => { /* … */ } , initialValue)
reduce((previousValue, currentValue, currentIndex) => { /* … */ } , initialValue)
array.reduce((previousValue, currentValue, currentIndex, array) => { /* … */ }, initialValue)//一个“reducer”函数，包含四个参数：
//previousValue：上一次调用 callbackFn 时的返回值。
//在第一次调用时，若指定了初始值 initialValue，其值则为 initialValue，
//否则为数组索引为 0 的元素 array[0]。//currentValue：数组中正在处理的元素。
//在第一次调用时，若指定了初始值 initialValue，其值则为数组索引为 0 的元素 array[0]，
//否则为 array[1]。//currentIndex：数组中正在处理的元素的索引。
//若指定了初始值 initialValue，则起始索引号为 0，否则从索引 1 起始。//array：用于遍历的数组。//initialValue 可选
//作为第一次调用 callback 函数时参数 previousValue 的值。
//若指定了初始值 initialValue，则 currentValue 则将使用数组第一个元素；
//否则 previousValue 将使用数组第一个元素，而 currentValue 将使用数组第二个元素。
const array1 = [1, 2, 3, 4];// 0 + 1 + 2 + 3 + 4
const initialValue = 0;
const sumWithInitial = array1.reduce((accumulator, currentValue) => accumulator + currentValue,initialValue
);console.log(sumWithInitial);
// Expected output: 10String(split/concat/substring/indexOf/includes)
输入str->arr：str.split(separator/reg).map(e=>Number(e))
str.substring(indexStart[, indexEnd])
str.indexOf(searchString[, position])
str.includes()
str.charAt(index)//获取第n位字符
str.charCodeAt(n)//获取第n位字符的UTF-16字符编码 （Unicode）A是65，a是97
String.fromCharCode(num1[, ...[, numN]])//根据UTF编码创建字符串String.fromCharCode('a'.charCodeAt(0))='a'str.trim()//返回去掉首尾的空白字符后的新字符串str.split(separator)//返回一个以指定分隔符出现位置分隔而成的一个数组，数组元素不包含分隔符const str = 'The quick brown fox jumps over the lazy dog.';const words = str.split(' ');
console.log(words[3]);
// Expected output: "fox"str.toLowerCase( )//字符串转小写；
str.toUpperCase( )//字符串转大写；str.concat(str2, [, ...strN])str.substring(indexStart[, indexEnd]) //提取从 indexStart 到 indexEnd（不包括）之间的字符。
str.substr(start[, length]) //没有严格被废弃 (as in "removed from the Web standards"), 但它被认作是遗留的函数并且可以的话应该避免使用。它并非 JavaScript 核心语言的一部分，未来将可能会被移除掉。str.indexOf(searchString[, position]) //在大于或等于position索引处的第一次出现。
str.match(regexp)//找到一个或多个正则表达式的匹配。
const paragraph = 'The quick brown fox jumps over the lazy dog. It barked.';
let regex = /[A-Z]/g;
let found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T", "I"]
regex = /[A-Z]/;
found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T"]//match类似 indexOf() 和 lastIndexOf()，但是它返回指定的值，而不是字符串的位置。
var str = '123123000'
str.match(/\w{3}/g).join(',') // 123,123,000str.search(regexp)//如果匹配成功，则 search() 返回正则表达式在字符串中首次匹配项的索引;否则，返回 -1
const paragraph = '? The quick';// Any character that is not a word character or whitespace
const regex = /[^\w\s]/g;console.log(paragraph.search(regex));
// Expected output: 0str.repeat(count)//返回副本
str.replace(regexp|substr, newSubStr|function)//返回一个由替换值（replacement）替换部分或所有的模式（pattern）匹配项后的新字符串。
const p = 'lazy dog.Dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replace('dog', 'monkey'));
// "lazy monkey.Dog lazy"let regex = /dog/i;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replace(regex, 'ferret'));
//"lazy ferret.Dog lazy"regex = /d|Dog/g;
console.log(p.replace(regex, 'ferret'));
//"lazy ferretog.ferret lazy"//当使用一个 regex 时，您必须设置全局（“g”）标志， 否则，它将引发 TypeError：“必须使用全局 RegExp 调用 replaceAll”。
const p = 'lazy dog.dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replaceAll('dog', 'monkey'));
// "lazy monkey.monkey lazy"let regex = /dog/g;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replaceAll(regex, 'ferret'));
//"lazy ferret.ferret lazy"正则表达式Regular Expression(RegExp)
str.match(regexp): [values]
str.search(regexp): idx
str.replace(regexp|substr, newSubStr|function)
修饰符：i大小写不敏感
边界量词：^首$尾
数组
折半 / 二分查找
判定树：描述 折半查找过程
ASLsucc≈log2(n+1)-1
keys: [L,R] while(L<=R)
螺旋矩阵*
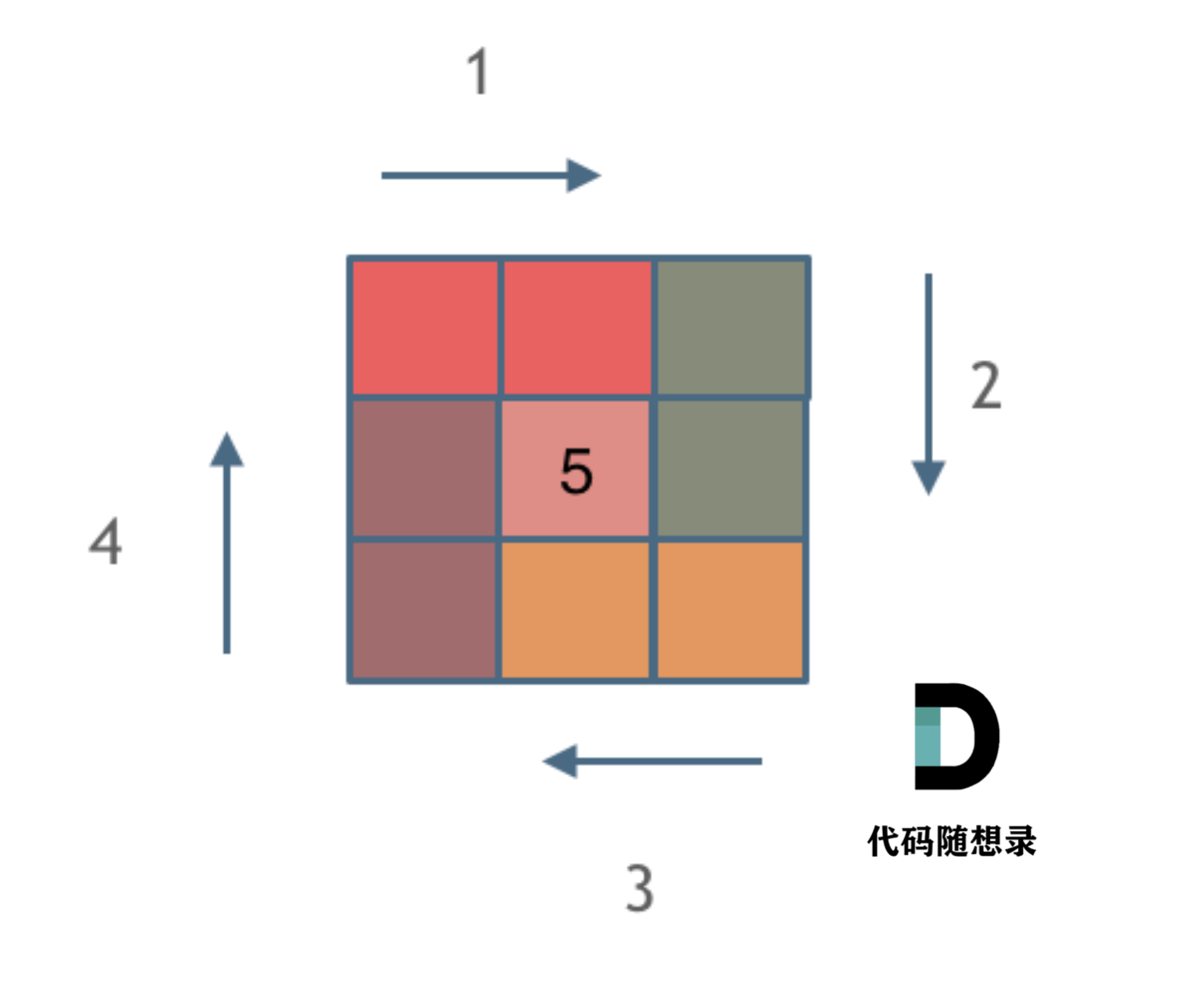
/*** @param {number} n* @return {number[][]}*/
var generateMatrix = function(n) {let startX = startY = 0; // 起始位置let loop = Math.floor(n/2); // 旋转圈数let mid = Math.floor(n/2); // 中间位置let offset = 1; // 控制每一层填充元素个数let count = 1; // 更新填充数字let res = new Array(n).fill(0).map(() => new Array(n).fill(0));while (loop--) {let row = startX, col = startY;// 上行从左到右（左闭右开）for (; col < startY + n - offset; col++) {res[row][col] = count++;}// 右列从上到下（左闭右开）for (; row < startX + n - offset; row++) {res[row][col] = count++;}// 下行从右到左（左闭右开）for (; col > startY; col--) {res[row][col] = count++;}// 左列做下到上（左闭右开）for (; row > startX; row--) {res[row][col] = count++;}// 更新起始位置startX++;startY++;// 更新offsetoffset += 2;}// 如果n为奇数的话，需要单独给矩阵最中间的位置赋值if (n % 2 === 1) {res[mid][mid] = count;}return res;
};旋转矩阵
行<->列，对角线
考前复习
应该尽可能多的看各种各样的题目，思考五分钟，想不出来解法的话直接看别人的答案。看懂思路就行了，甚至自己写一遍都没必要，因为比较浪费时间。
笔试的时候最怕的是没思路，所以把各种题型都过目一下，起码心里不会慌，只要有思路，平均一道题二三十分钟搞定还是不难的
mirrors / labuladong / Fucking Algorithm · GitCode
推荐：labuladong 的算法小抄 | labuladong 的算法小抄
突击笔试计划
mirrors / youngyangyang04 / leetcode-master · GitCode
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！