Codeforces-1687 A: The Enchanted Forest

题目

题目截图

样例描述

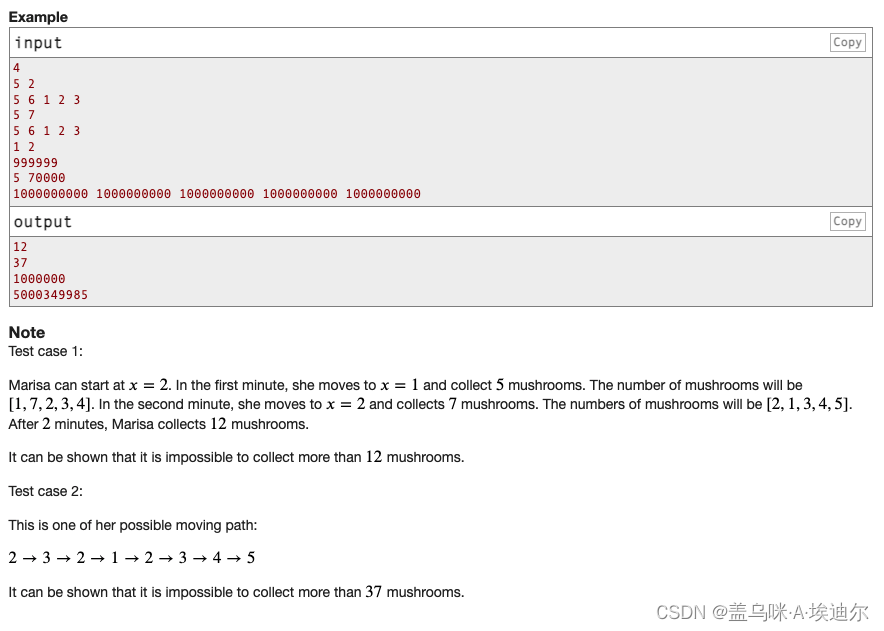
题目大意

  给定一个长度为 $n$ 的数组 { a i } \{a_i\} {ai​}。
  可以选定数组中的任何位置为初始点，在每一步，以下三个动作顺序发生：
    1. 从当前位置 $x$ 移动到位置 $y$。($|x-y|\le 1$，注意可以不动)
    2. 拿走 $y$ 位置上的值，加入答案。
    3. 数组上每个位置的值 $+1$。
  一共可以走 $k$ 步，问答案的最大值是多少。

题目解析

  很容易想到，这个题目 $k$ 和 $n$ 的大小决定了答案走向。
  $k<=n$ 时，我们不可能往回走，因为在行进的过程中，已经走过的点相当于初始的值已经被拿完了，而新增的值，没走过的值一定大于走过的值，因此，我们直接找整个数组中值和最大的连续一段，顺便再加上新增的值 $k(k-1)/2$ 即可。
  而 $k>n$ 时，首先能想到的是我们能把初始值拿完，肯定都要拿走，那么之后的问题就是怎样走能够让答案值尽可能的大，换句话说，让走完之后残留的值尽可能的小。我们设当前还有 $i$ 步可以走，那么每走一步，我们就会最少有 $n-i$ 个浪费值（因为这些加在到不了的 $n-i$ 个值上，如果在过程中我们重复移动，那么这个浪费值会更大），那么总的浪费值最小为 ∑ i = 0 n − 1 ( n − i ) = n ( n + 1 ) / 2 \sum_{i=0}^{n-1} (n-i)= n(n+1)/ 2 ∑i=0n−1​(n−i)=n(n+1)/2。因此，我们把过程中总的新增值减去这个数，再加上初始值就是最终答案。
  第二种情况的实例还是很好想的。我们可以从头开始拿完所有初始值，再在尾窝到正好结尾能拿完，然后再走到头，步数正好用完，浪费值也是 $n(n+1)/2$，当然，这只是特例，只要拿完应有的，减少浪费都可以当实例。

Code

#include 
using namespace std;typedef long long LL;
const int maxn = 2e5 + 7;
int a[maxn]; LL p[maxn];int main() {int t, n, k;cin >> t;while(t--) {cin >> n >> k;for(int i=1; i<=n; ++i) {cin >> a[i];p[i] = p[i-1] + a[i];}if(n >= k) {LL ans = 0;for(int i=k; i<=n; ++i)ans = max(ans, p[i] - p[i-k]);cout << ans + 1ll * k * (k - 1) / 2 << endl;} else {LL ans = p[n];cout << ans - 1ll * n * (-k * 2  + n + 1) / 2 << endl;}}return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！