直线与平面方程的几何表达

法向量求法

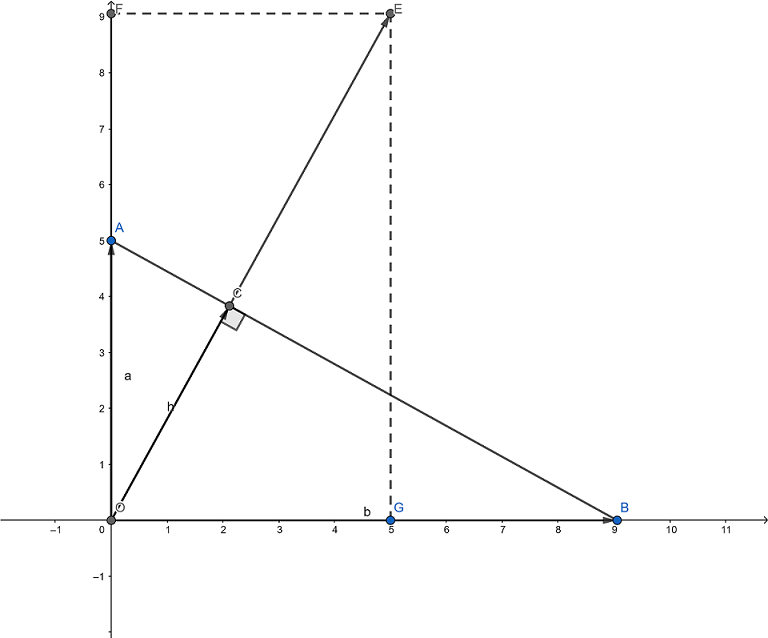
已知直线AB与坐标轴交于A，B两点，OA长为a, OB长为b，求AB的方程.

直线的特征是其上的点与直线法向量的点乘是固定的
E的坐标为 (a,b) 显然OE是直线的一法向量

a x + b y = h ⃗ ⋅ O E ⃗ = ∣ h ⃗ ∣ ⋅ ∣ O E ⃗ ∣ = ∣ h ⃗ ∣ ⋅ ∣ A B ⃗ ∣ = 2 S O A B = a b ax + by = \vec{h} \cdot \vec {OE} = |\vec{h}| \cdot |\vec {OE}| = |\vec{h}| \cdot |\vec {AB}| = 2 S_{OAB} = ab ax+by=h ⋅OE =∣h ∣⋅∣OE ∣=∣h ∣⋅∣AB ∣=2SOAB​=ab

所以
$$ax+by=ab$$

面积求法

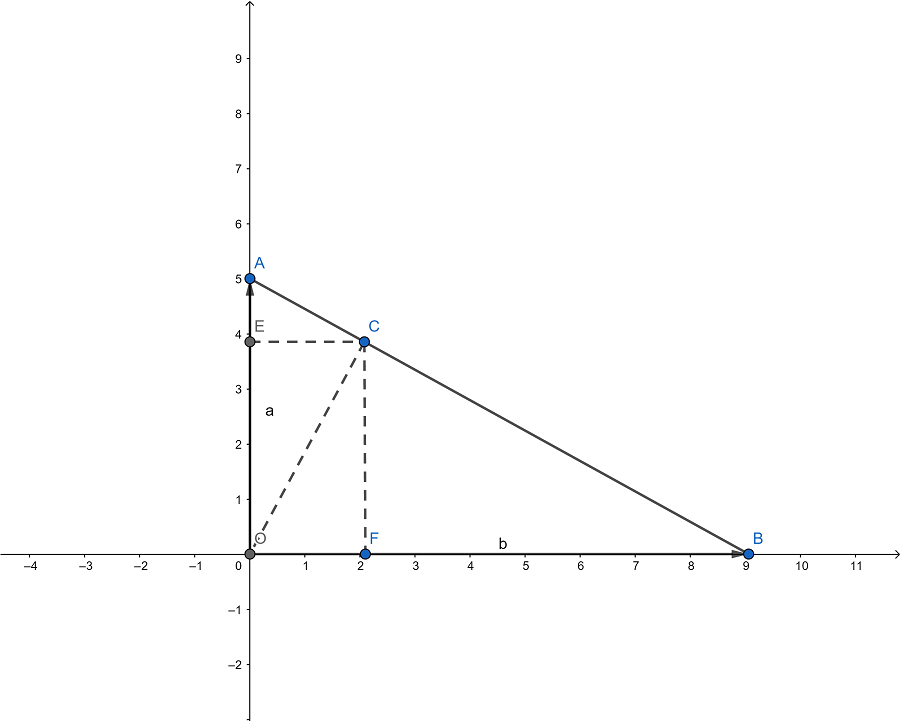
C是直线AB上的点，于是有

S O A C + S O C B = S O A B S_{OAC} + S_{OCB} = S_{OAB} SOAC​+SOCB​=SOAB​

即
$ax+by=ab$

向量叉乘求法

只要 A ⃗ \vec{A} A , B ⃗ \vec{B} B 不平行，
C ⃗ \vec{C} C 就可以写成(1):

C ⃗ = a A ⃗ + b B ⃗ \vec{C} = a\vec{A} + b\vec{B} C =aA +bB

又因C在AB的连线上，根据面积关系，有(2):

A ⃗ × B ⃗ = A ⃗ × C ⃗ + C ⃗ × B ⃗ \vec{A} \times \vec{B} = \vec{A} \times \vec{C} + \vec{C} \times \vec{B} A ×B =A ×C +C ×B

将(1)式，代入(2)式，有:

A ⃗ × B ⃗ = A ⃗ × ( a A ⃗ + b B ⃗ ) + ( a A ⃗ + b B ⃗ ) × B ⃗ \vec{A} \times \vec{B} = \vec{A} \times ( a\vec{A} + b\vec{B} ) + ( a\vec{A} + b\vec{B} ) \times \vec{B} A ×B =A ×(aA +bB )+(aA +bB )×B
A ⃗ × B ⃗ = A ⃗ × b B ⃗ + a A ⃗ × B ⃗ \vec{A} \times \vec{B} = \vec{A} \times b\vec{B} + a\vec{A} \times \vec{B} A ×B =A ×bB +aA ×B
A ⃗ × B ⃗ = ( a + b ) A ⃗ × B ⃗ \vec{A} \times \vec{B} = (a+b)\vec{A} \times \vec{B} A ×B =(a+b)A ×B
$$1=a+b$$

非常关键的是，这法可以将 A ⃗ \vec{A} A , B ⃗ \vec{B} B 推广到平面上任意两个不平行向量，而不只限于坐标轴.

面积求法-平面方程

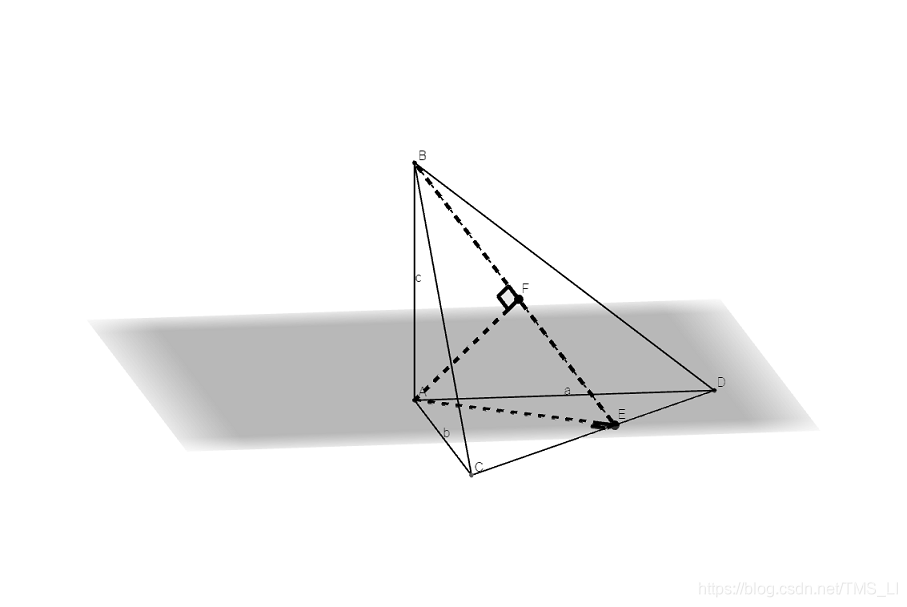
F为平面BCD上的一点，于是有

S F A B C + S F A C D + S F A D B + = S A B C D S_{FABC} + S_{FACD} + S_{FADB} + =S_{ABCD} SFABC​+SFACD​+SFADB​+=SABCD​

即
$bcx+acy+abz=abc$

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！