多边形面积(difficult)

Description

中学生杰利陶醉于数学研究．他思考的问题对于专家而言可能太多简单，但作为一个15岁的业余爱好者，他做得非常棒．他太热衷思考数学问题，以至于轻易就学会了试用数学方法来解决碰到的问题．一天，他看到桌上的一张纸．他四岁的妹妹玛利在上央画了一些线．那些线恰好构成了一个凹多边形，如下图：

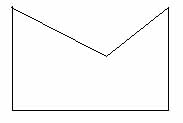
＂棒极了＂，他想，＂这些多边形看起来是规则的．我曾经学过怎样计算三角形、矩形和圆形的面积。我一定能找到计算这些图形的方法。＂他确实做到了。首先，他标记多边形顶点的坐标。如图二所示。随后，他毫不费力的求得结果0.75。

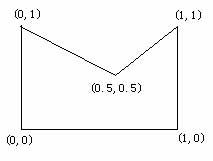
当然，他不会满足解决这样简单的问题。“嗯，如果纸上面是任意一个多边形，我们应该怎样计算它的面积呢？”他问自己。可他一直都没有找到计算多边形面积的通用方法。他清楚地明白以他的能力无法找到总是的答案。所以他向你请教。他会很感谢你的好心帮助。

Input

第一行是一个整数n，代表图形的顶点数（１＜＝n＜＝１０００）．
接下来的n行，每行一对实数，代表顶点坐标(xi,yi)。每个样例的图形由第一个顶点连接第二个顶点，第二个顶点连接第三个顶点…最后第n个顶点连接第一个顶点形成封闭多边形。

Output

输出图形面积或字符串"Impossible"
如果图形是一个多边形，计算他的面积（精确到小数点后两位）。如果输入的顶点不能构成多边形（也就是说，一条边和另一条边不相连的边相交，例如，四条线段的图形，第一条线段和第三条线段相交），就输出"Impossible"。指出图形不可能是多边形。如果顶点的数量不足以构成一个封闭的多边形，也输出"Impossible"

Hint

GDKOI2002-5
对于求多边形的面积（无论凹凸），同样可能和叉积．设多边形顶点依次为A1,A2,A3,．．．,AN，则该多边形面积为:
A1A2A1A3+A1A3A1A4+…+A1An-1*AN

输入样例

1

5
0 0
0 1
0.5 0.5
1 1
1 0

2

4
0 0 
0 1
1 0
1 1

输出样例

1

0.75

2

Impossible

解题思路

参考【51nod 1264】线段相交（计算几何）和P2785 物理1（phsic1）- 磁通量（计算几何）

AC代码

#include
#include
#include
using namespace std;
int n;
double ans,x[1005],y[1005];
struct node
{double x,y;
}a[5];
double cj(node x,node y,node z)
{return (x.x-z.x)*(y.y-z.y)-(x.y-z.y)*(y.x-z.x);
}
bool check(node x,node y,node z)
{if(z.x>=min(x.x,y.x)&&z.x<=max(x.x,y.x)&&z.y>=min(x.y,y.y)&&z.y<=max(x.y,y.y))return 1;return 0;
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++)scanf("%lf%lf",&x[i],&y[i]);if(n<3){printf("Impossible");return 0;}for(int i=1;i<n;i++)for(int j=i+2;j<=n;j++){if(i==1&&j==n)continue;int t=j+1;if(t>n)t=1;a[1]=(node){x[i],y[i]};a[2]=(node){x[i+1],y[i+1]};a[3]=(node){x[j],y[j]};a[4]=(node){x[t],y[t]};int ok=0;if(cj(a[3],a[4],a[1])*cj(a[3],a[4],a[2])<0&&cj(a[1],a[2],a[3])*cj(a[1],a[2],a[4])<0)ok=1;if(!cj(a[1],a[2],a[3])&&check(a[1],a[2],a[3]))ok=1;if(!cj(a[1],a[2],a[4])&&check(a[1],a[2],a[4]))ok=1;if(!cj(a[3],a[4],a[1])&&check(a[3],a[4],a[1]))ok=1;if(!cj(a[3],a[4],a[2])&&check(a[3],a[4],a[2]))ok=1;if(ok){printf("Impossible");return 0;}}for(int i=1;i<n;i++)ans+=(x[i]*y[i+1]-x[i+1]*y[i])/2.0;ans+=(x[n]*y[1]-x[1]*y[n])/2.0;printf("%.2lf",abs(ans));return 0;
} 

谢谢

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！